黄冈中学自主招生考试数学试卷.doc

黄冈中学自主招生考试数学试卷.doc

《黄冈中学自主招生考试数学试卷.doc》由会员分享，可在线阅读，更多相关《黄冈中学自主招生考试数学试卷.doc（23页珍藏版）》请在冰豆网上搜索。

2017年湖北省黄冈中学自主招生数学试卷

一、填空题（每小题5分，共40分）

1．（5分）方程组的解是　　．

2．（5分）若对任意实数x不等式ax＞b都成立，那么a，b的取值范围为　　．

3．（5分）设﹣1≤x≤2，则|x﹣2|﹣|x|+|x+2|的最大值与最小值之差为　　．

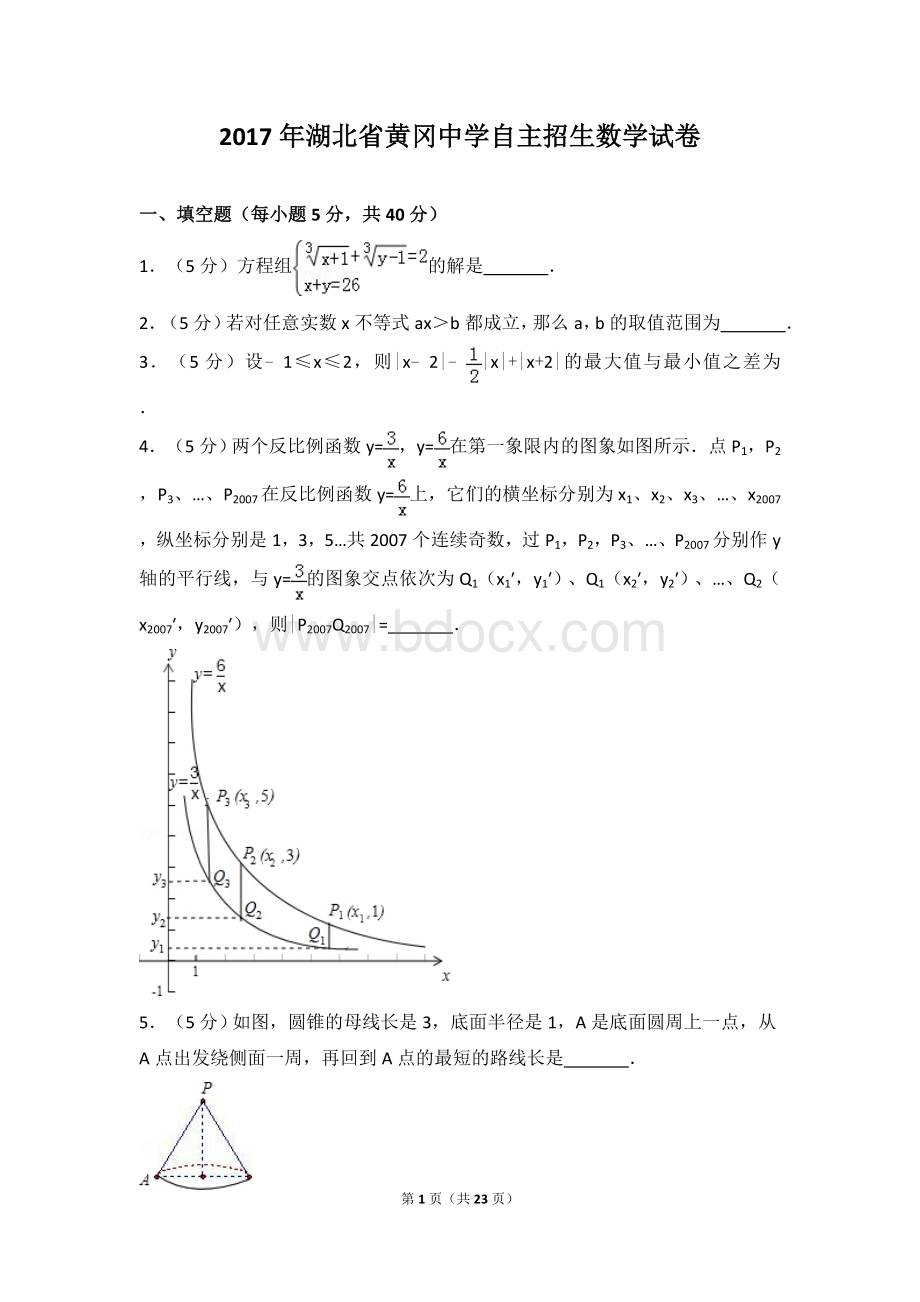
4．（5分）两个反比例函数y=，y=在第一象限内的图象如图所示．点P1，P2，P3、…、P2007在反比例函数y=上，它们的横坐标分别为x1、x2、x3、…、x2007，纵坐标分别是1，3，5…共2007个连续奇数，过P1，P2，P3、…、P2007分别作y轴的平行线，与y=的图象交点依次为Q1（x1′，y1′）、Q1（x2′，y2′）、…、Q2（x2007′，y2007′），则|P2007Q2007|=　　．

5．（5分）如图，圆锥的母线长是3，底面半径是1，A是底面圆周上一点，从A点出发绕侧面一周，再回到A点的最短的路线长是　　．

6．（5分）有一张矩形纸片ABCD，AD=9，AB=12，将纸片折叠使A、C两点重合，那么折痕长是　　．

7．（5分）已知3，a，4，b，5这五个数据，其中a，b是方程x2﹣3x+2=0的两个根，则这五个数据的标准差是　　．

8．（5分）若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点，则定点坐标为　　．

二、选择题（每小题5分，共40分）

9．（5分）如图，△ABC中，D、E是BC边上的点，BD：

DE：

EC=3：

2：

1，M在AC边上，CM：

MA=1：

2，BM交AD，AE于H，G，则BH：

HG：

GM等于（　　）

A．3：

2：

1 B．5：

3：

1 C．25：

12：

5 D．51：

24：

10

10．（5分）若一直角三角形的斜边长为c，内切圆半径是r，则内切圆的面积与三角形面积之比是（　　）

A． B． C． D．

11．（5分）抛物线y=ax2与直线x=1，x=2，y=1，y=2围成的正方形有公共点，则实数a的取值范围是（　　）

A．≤a≤1 B．≤a≤2 C．≤a≤1 D．≤a≤2

12．（5分）有铅笔、练习本、圆珠笔三种学习用品，若购铅笔3支，练习本7本，圆珠笔1支共需3.15元；若购铅笔4支，练习本8本，圆珠笔2支共需4.2元，那么，购铅笔、练习本、圆珠笔各1件共需（　　）

A．1.2元 B．1.05元 C．0.95元 D．0.9元

13．（5分）设关于x的方程ax2+（a+2）x+9a=0，有两个不相等的实数根x1、x2，且x1＜1＜x2，那么实数a的取值范围是（　　）

A． B． C． D．

14．（5分）如图，正方形ABCD的边AB=1，和都是以1为半径的圆弧，则无阴影两部分的面积之差是（　　）

A． B．1﹣ C．﹣1 D．1﹣

15．（5分）已知锐角三角形的边长是2，3，x，那么第三边x的取值范围是（　　）

A．1＜x＜ B． C． D．

16．（5分）某工厂第二季度的产值比第一季度的产值增长了x%，第三季度的产值又比第二季度的产值增长了x%，则第三季度的产值比第一季度的产值增长了（　　）

A．2x% B．1+2x% C．（1+x%）x% D．（2+x%）x%

三、解答题（共40分）

17．（7分）设m是不小于﹣1的实数，关于x的方程x2+2（m﹣2）x+m2﹣3m+3=0有两个不相等的实数根x1、x2，

（1）若x12+x22=6，求m值；

（2）求的最大值．

18．（7分）如图，开口向下的抛物线y=ax2﹣8ax+12a与x轴交于A、B两点，抛物线上另有一点C在第一象限，且使△OCA∽△OBC，

（1）求OC的长及的值；

（2）设直线BC与y轴交于P点，点C是BP的中点时，求直线BP和抛物线的解析式．

19．（7分）某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按120个工时计算）生产空调器、彩电、冰箱共360台，且冰箱至少生产60台，已知生产这些家电产品每台所需工时和每台产值如下表：

家电名称

空调

彩电

冰箱

工时

产值（千元）

4

3

2

问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高最高产值是多少？

（以千元为单位）

20．（9分）一个家庭有3个孩子，

（1）求这个家庭有2个男孩和1个女孩的概率；

（2）求这个家庭至少有一个男孩的概率．

21．（10分）如图，已知⊙O和⊙O′相交于A、B两点，过点A作⊙O′的切线交⊙O于点C，过点B作两圆的割线分别交⊙O、⊙O′于E、F，EF与AC相交于点P．

（1）求证：

PA•PE=PC•PF；

（2）求证：

；

（3）当⊙O与⊙O′为等圆时，且PC：

CE：

EP=3：

4：

5时，求△PEC与△FAP的面积的比值．

2017年湖北省黄冈中学自主招生数学试卷

参考答案与试题解析

一、填空题（每小题5分，共40分）

1．（5分）方程组的解是　和　．

【分析】根据式子特点，设x+1=a，y﹣1=b，然后利用换元法将原方程组转化为关于a、b的方程组，再换元为关于x、y的方程组解答．

【解答】解：

设x+1=a，y﹣1=b，则原方程可变为，

由②式又可变化为=26，

把①式代入得=13，这又可以变形为（+）2﹣3=13，

再代入又得﹣3=9，

解得ab=﹣27，

又因为a+b=26，

所以解这个方程组得或，

于是

（1），解得；

（2），解得．

故答案为和．

【点评】本题主要考查解无理方程的知识点，去掉根号把无理式化成有理方程是解题的关键，需要同学们仔细掌握．

2．（5分）若对任意实数x不等式ax＞b都成立，那么a，b的取值范围为　a=0，b＜0　．

【分析】分a=0，a≠0两种情况分析．

【解答】解：

∵如果a≠0，不论a大于还是小于0，对任意实数x不等式ax＞b都成立是不可能的，

∴a=0，则左边式子ax=0，

∴b＜0一定成立，

∴a，b的取值范围为a=0，b＜0．

【点评】本题是利用了反证法的思想．

3．（5分）设﹣1≤x≤2，则|x﹣2|﹣|x|+|x+2|的最大值与最小值之差为　1　．

【分析】先根据﹣1≤x≤2，确定x﹣2与x+2的符号，在对x的符号进行讨论即可．

【解答】解：

∵﹣1≤x≤2，∴x﹣2≤0，x+2＞0，

∴当2≥x≥0时，|x﹣2|﹣|x|+|x+2|=2﹣x﹣x+x+2=4﹣x；

当﹣1≤x＜0时，|x﹣2|﹣|x|+|x+2|=2﹣x+x+x+2=4+x，

当x=0时，取得最大值为4，x=2时取得最小值，最小值为3，

则最大值与最小值之差为1．

故答案为：

1

【点评】本题重点考查有理数的绝对值和求代数式值．解此类题的关键是：

先利用条件判断出绝对值符号里代数式的正负性，再根据绝对值的性质把绝对值符号去掉，把式子化简，即可求解．

4．（5分）两个反比例函数y=，y=在第一象限内的图象如图所示．点P1，P2，P3、…、P2007在反比例函数y=上，它们的横坐标分别为x1、x2、x3、…、x2007，纵坐标分别是1，3，5…共2007个连续奇数，过P1，P2，P3、…、P2007分别作y轴的平行线，与y=的图象交点依次为Q1（x1′，y1′）、Q1（x2′，y2′）、…、Q2（x2007′，y2007′），则|P2007Q2007|=　　．

【分析】要求出|P2007Q2007|的值，就要先求|Qy2007﹣Py2007|的值，因为纵坐标分别是1，3，5…，共2007个连续奇数，其中第2007个奇数是2×2007﹣1=4013，所以P2007的坐标是（Px2007，4013），那么可根据P点都在反比例函数y=上，可求出此时Px2007的值，那么就能得出P2007的坐标，然后将P2007的横坐标代入y=中即可求出Qy2007的值．那么|P2007Q2007|=|Qy2007﹣Py2007|，由此可得出结果．

【解答】解：

由题意可知：

P2007的坐标是（Px2007，4013），

又∵P2007在y=上，

∴Px2007=．

而Qx2007（即Px2007）在y=上，所以Qy2007===，

∴|P2007Q2007|=|Py2007﹣Qy2007|=|4013﹣|=．

故答案为：

．

【点评】本题的关键是找出P点纵坐标的规律，以这个规律为基础求出P2007的横坐标，进而求出Q2007的值，从而可得出所求的结果．

5．（5分）如图，圆锥的母线长是3，底面半径是1，A是底面圆周上一点，从A点出发绕侧面一周，再回到A点的最短的路线长是　3　．

【分析】圆锥的侧面展开图是扇形，从A点出发绕侧面一周，再回到A点的最短的路线即展开得到的扇形的弧所对弦，转化为求弦的长的问题．

【解答】解：

∵图中扇形的弧长是2π，根据弧长公式得到2π=

∴n=120°即扇形的圆心角是120°

∴弧所对的弦长是2×3sin60°=3

【点评】正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．

6．（5分）有一张矩形纸片ABCD，AD=9，AB=12，将纸片折叠使A、C两点重合，那么折痕长是　　．

【分析】首先由勾股定理求出AC的长，设AC的中点为E，折线与AB交于F．然后求证△AEF∽△ABC求出EF的长．

【解答】解：

如图，由勾股定理易得AC=15，设AC的中点为E，折线FG与AB交于F，（折线垂直平分对角线AC），AE=7.5．

∵∠AEF=∠B=90°，∠EAF是公共角，

∴△AEF∽△ABC，

∴==．

∴EF=．

∴折线长=2EF=．

故答案为．

【点评】本题综合考查了矩形的性质，勾股定理，相似，全等等知识点．

7．（5分）已知3，a，4，b，5这五个数据，其中a，b是方程x2﹣3x+2=0的两个根，则这五个数据的标准差是　　．

【分析】先解方程得到a，b的值，计算出平均数和方差后，再计算方差的算术平方根，即为标准差．

【解答】解：

由方程x2﹣3x+2=0

解方程的两个根是1，2，即a=1，b=2

故这组数据是3，1，4，2，5

其平均数（3+1+4+2+5）=3

方差S2=[（3﹣3）2+（1﹣3）2+（4﹣3）2+（2﹣3）2+（5﹣3）2]=2

故五个数据的标准差是S==

故本题答案为：

．

【点评】计算标准差需要先算出方差，计算方差的步骤是：

（1）计算数据的平均数；

（2）计算偏差，即每个数据与平均数的差；

（3）计算偏差的平方和；

（4）偏差的平方和除以数据个数．

标准差即方差的算术平方根；

注意标准差和方差一样都是非负数．

8．（5分）若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点，则定点坐标为　（4，33）　．

【分析】把含p的项合并，只有当p的系数为0时，不管p取何值抛物线都通过定点，可求x、y的对应值，确定定点坐标．

【解答】解：

y=2x2﹣px+4p+1可化为y=2x2﹣p（x﹣4）+1，

分析可得：

当x=4时，y=33；且与p的取值无关；

故不管p取何值时都通过定点（4，33）．

【点评】本题考查二次函数图象过定点问题，解决此类问题：

首先根据题意，化简函数式，提出未知的常数，化简后再根据具体情况判断．

二、选择题（每小题5分，共40分）

9．（5分）如图，△ABC中，D、E是BC边上的点，BD：

DE：

EC=3：

2：

1，M在AC边上，CM：

MA=1：

2，BM交AD，AE于H，G，则BH：

HG：

GM等于（　　）

A．3：

2：

1 B．5：

3：

1 C．25：

12：

5 D．51：

24：

10

【分析】连接EM，根据已知可得△BHD∽△BME，△CEM∽△CDA，根据相似比从而不难得到答案