平面直角坐标系中的面积问题.doc

平面直角坐标系中的面积问题.doc

《平面直角坐标系中的面积问题.doc》由会员分享，可在线阅读，更多相关《平面直角坐标系中的面积问题.doc（5页珍藏版）》请在冰豆网上搜索。

复习：

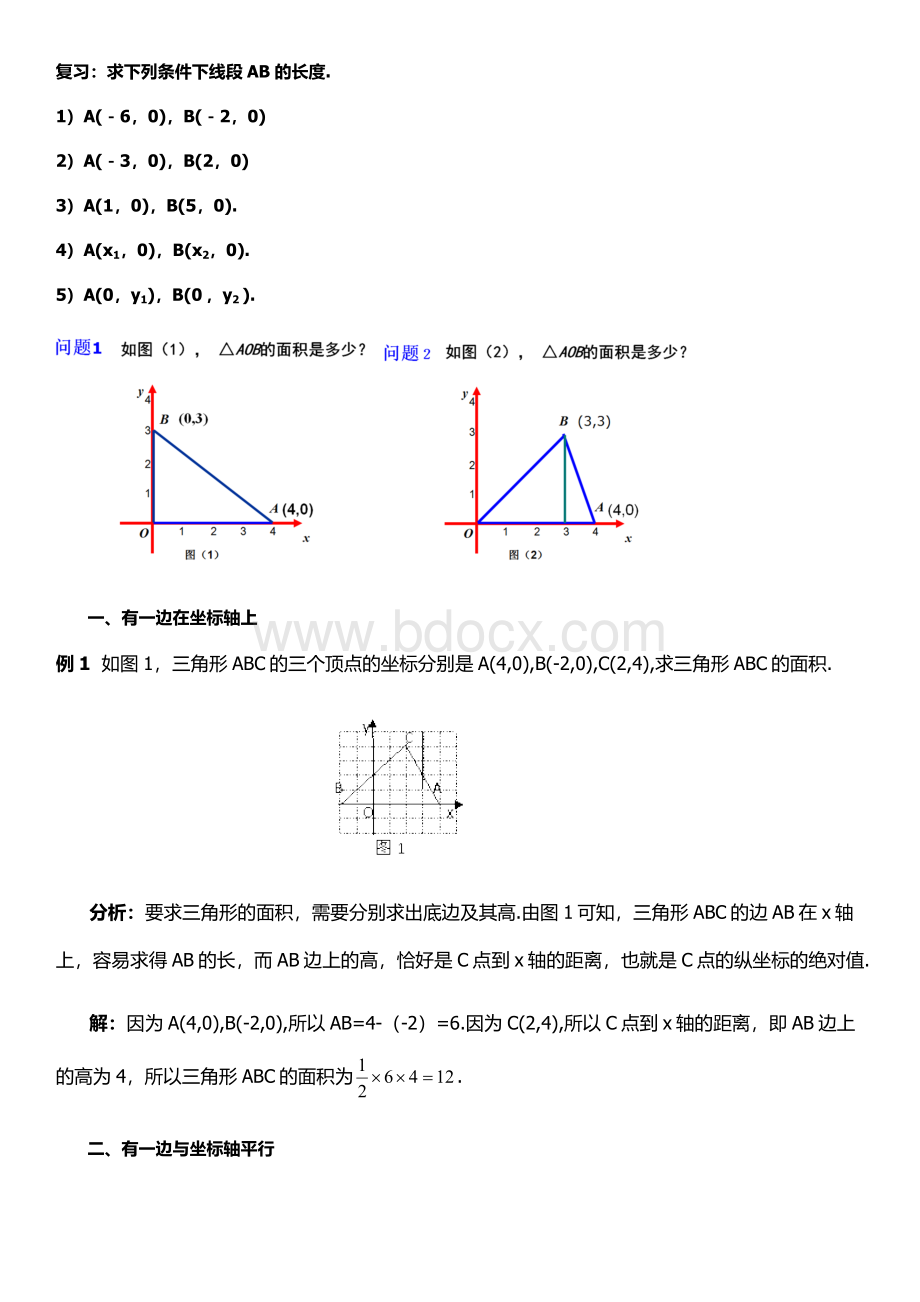
求下列条件下线段AB的长度.

1）A（－6，0），B（－2，0）

2）A（－3，0），B（2，0）

3）A（1，0），B（5，0）.

4）A（x1，0），B（x2，0）.

5）A（0，y1），B（0，y2）.

一、有一边在坐标轴上

例1如图1，三角形ABC的三个顶点的坐标分别是A（4,0）,B（-2,0）,C（2,4）,求三角形ABC的面积.

分析：

要求三角形的面积，需要分别求出底边及其高.由图1可知，三角形ABC的边AB在x轴上，容易求得AB的长，而AB边上的高，恰好是C点到x轴的距离，也就是C点的纵坐标的绝对值.

解：

因为A（4,0）,B（-2,0）,所以AB=4-（-2）=6.因为C（2,4）,所以C点到x轴的距离，即AB边上的高为4，所以三角形ABC的面积为.

二、有一边与坐标轴平行

例2如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.

分析：

由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.

解：

因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4.作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以三角形ABC的面积为.

三、三边均不与坐标轴平行

提高题：