与圆有关的专题综合讲义(六).doc

与圆有关的专题综合讲义(六).doc

《与圆有关的专题综合讲义(六).doc》由会员分享，可在线阅读，更多相关《与圆有关的专题综合讲义(六).doc（16页珍藏版）》请在冰豆网上搜索。

与圆有关的专题综合讲义（六）

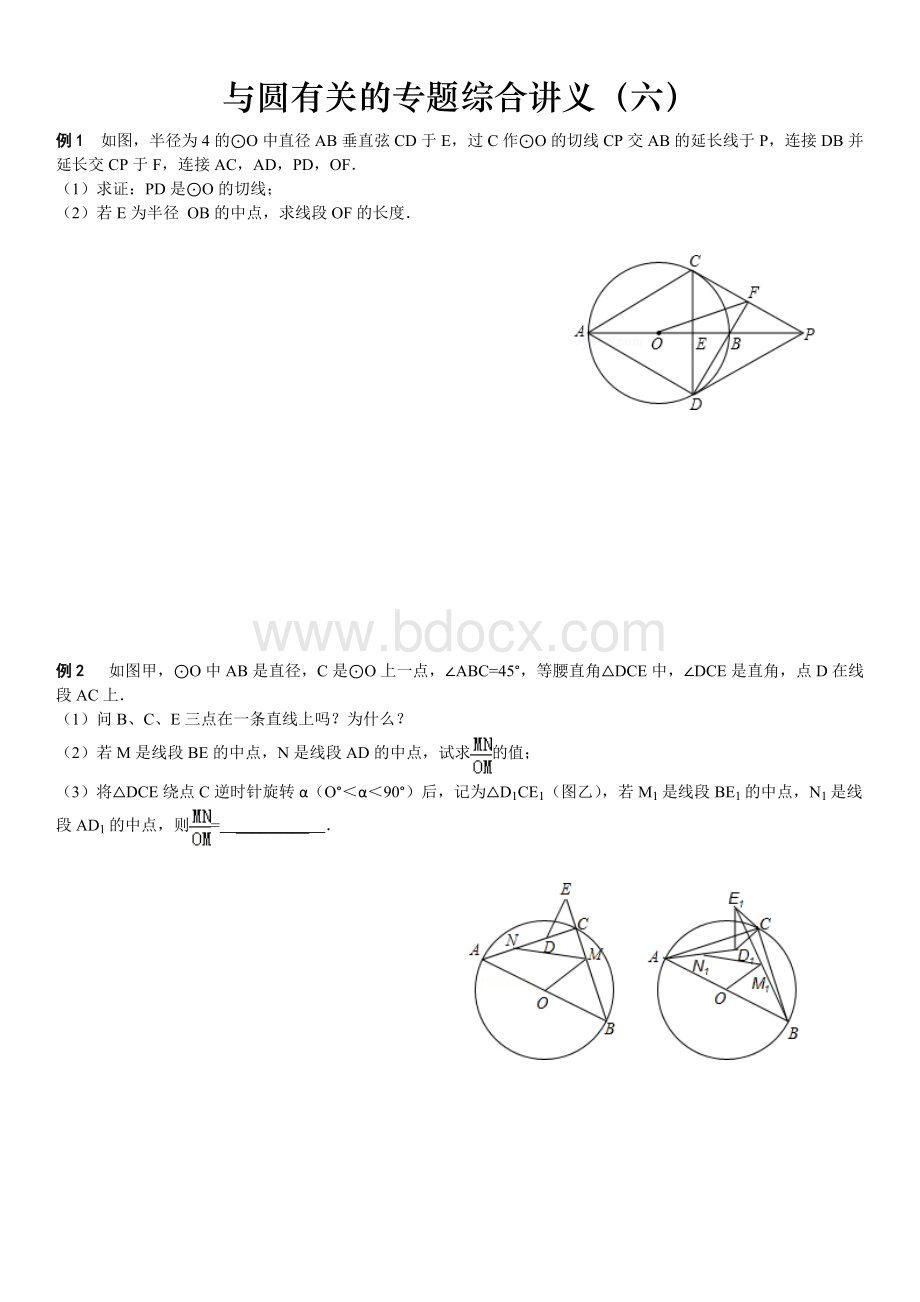
例1如图，半径为4的⊙O中直径AB垂直弦CD于E，过C作⊙O的切线CP交AB的延长线于P，连接DB并延长交CP于F，连接AC，AD，PD，OF．

（1）求证：

PD是⊙O的切线；

（2）若E为半径OB的中点，求线段OF的长度．

例2如图甲，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角△DCE中，∠DCE是直角，点D在线段AC上．

（1）问B、C、E三点在一条直线上吗？

为什么？

（2）若M是线段BE的中点，N是线段AD的中点，试求的值；

（3）将△DCE绕点C逆时针旋转α（O°＜α＜90°）后，记为△D1CE1（图乙），若M1是线段BE1的中点，N1是线段AD1的中点，则=　_________　．

例3如图1，在平面直角坐标系中，半径为4的⊙O交坐标轴于A、B、C、D，点P为BC上一个动点（不与B、C点重合）．连AP、BC交于点G，连FG交OB于点E．

（1）请运用圆的定义证明C、F、P、G在同一个圆上；

（2）当P为BC的中点时，求点G的坐标；

（3）如图2，连接PD，设△PAB的内切圆半径为r，求证：

．

例4如图，已知BC是⊙O的直径，P是⊙O上一点，A是的中点，AD⊥BC于点D，BP与AD相交于点E．

（1）当BC=6且∠ABC=60°时，求的长；

（2）求证：

AE=BE．

（3）过A点作AM∥BP，求证：

AM是⊙O的切线．

例5如图，在△ABC中，AB=BC．以AB为直径作圆⊙O交AC于点D，点E为⊙O上一点，连接ED并延长与BC的延长线交于点F．连接AE、BE，∠BAE=60°，∠F=15°，解答下列问题．

（1）求证：

直线FB是⊙O的切线；

（2）若BE=cm，则AC=　_________　cm．

例6如图

（1），直线y=kx+1与y轴正半轴交于A，与x轴正半轴交于B，以AB为边作正方形ABCD．

（1）若C（3，m），求m的值；

（2）如图2，连AC，作BM⊥AC于M，E为AB上一点，CE交BM于F，若BE=BF，求证：

AC+AE=2AB；

（3）经过B、C两点的⊙O1交AC于S，交AB的延长线于T，当⊙O1的大小发生变化时，的值变吗？

若不变证明并求其值；若变化，请说明理由．

例7如图，E点为x轴正半轴上一点，⊙E交x轴于A、B两点，交y轴于C、D两点，P点为劣弧上一个动点，且A（﹣1，0），E（1，0）．

（1）如图1，求点C的坐标；

（2）如图2，连接PA，PC．若CQ平分∠PCD交PA于Q点，当P点在运动时，线段AQ的长度是否发生变化；若不变求出其值，若发生变化，求出变化的范围；

（3）如图3，连接PD，当P点在运动时（不与B、C两点重合），给出下列两个结论：

①的值不变，②的值不变，其中有且只有一个是正确的，请你判断哪一个是正确的，并求其值．

例8如图①，直线AB的解析式为y=kx﹣2k（k＜0）与x轴、y轴分别交于A、B两点，∠ABO=60°．经过A、O两点的⊙O1与x轴的负半轴交于点C，与直线AB切于点A．

（1）求C点的坐标；

（2）如图②，过O1作直线EF∥y轴，在直线EF上是否存在一点D，使得△DAB的周长最短，若存在，求出D点坐标，不存在，说明理由；

（3）在

（2）的条件下，连接OO1与⊙O1交于点G，点P为劣弧GF上一个动点，连接GP与EF的延长线交于H点，连接EP与OG交于I点，当P在劣弧GF运动时（不与G、F两点重合），O1H﹣O1I的值是否发生变化，若不变，求其值，若发生变化，求出其值的变化范围．

与圆有关的专题综合讲义（六）

参考答案与试题解析

1．如图，半径为4的⊙O中直径AB垂直弦CD于E，过C作⊙O的切线CP交AB的延长线于P，连接DB并延长交CP于F，连接AC，AD，PD，OF．

（1）求证：

PD是⊙O的切线；

（2）若E为半径OB的中点，求线段OF的长度．

考点：

切线的判定与性质；等边三角形的判定与性质．1125860

分析：

（1）连接OD、OC．欲证PD是⊙O的切线，只需证明OD⊥PD即可；通过全等三角形△COP≌△DOP（SAS）的对应角∠OCP=∠ODP=90°来证明该结论；

（2）利用等边三角形的判定知△ODB和△PCD均为等边三角形，然后由等边三角形的“三线合一”的性质、勾股定理求得OF的长度．

解答：

（1）证明：

连接OD、OC．

∵OC=OD（⊙O的半径），AB是直径，直径AB⊥弦CD（已知），

∴OE是∠COD的平分线，

∴∠COE=∠DOE；

在△COP和△DOP中，

∵，

∴△COP≌△DOP（SAS），

∴∠OCP=∠ODP（全等三角形的对应角相等）；

又∵CP是⊙O的切线，

∴∠OCP=90°（切线的性质），

∴∠ODP=90°（等量代换），

∵点D在⊙O上，

∴PD是⊙O的切线；

（2）解：

∵CD⊥AB，点E是OB的中点，

∴OD=BD；

又∵OB=OD，

∴OB=OD=BD，

∴△BOD是等边三角形，

∴∠ODB=60°，

∴∠ODE=∠BDE=30°（等腰三角形的“三线合一”的性质），

∵OD=4，

∴DE=OD•sin∠DOE=，

∴CD=2DE=4；

∵∠ODP=90°，

∴∠CDP=60°；

∵PC、PD是⊙O的两条切线，

∴PC=PD，

∴△PCD是等边三角形（有一内角为60°的等腰三角形是等边三角形），

∴CD=PD，

∴点F是PC的中点；

在Rt△CDF中，CD=4，∠CDF=30°，则CF=CD=2（30°角所对的直角边是斜边的一半）；

在Rt△OCF中，OF=（勾股定理）．

点评：

本题综合考查了切线的判定与性质、全等三角形的判定与性质以及等边三角形的判定与性质．有一内角为60°的等腰三角形是等边三角形．

2．如图甲，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角△DCE中，∠DCE是直角，点D在线段AC上．

（1）问B、C、E三点在一条直线上吗？

为什么？

（2）若M是线段BE的中点，N是线段AD的中点，试求的值；

（3）将△DCE绕点C逆时针旋转α（O°＜α＜90°）后，记为△D1CE1（图乙），若M1是线段BE1的中点，N1是线段AD1的中点，则=　　．

考点：

圆周角定理；平行线的判定；等腰直角三角形；相似三角形的判定与性质．1125860

分析：

（1）根据直径所对的圆周角为直角得到∠BCA=90°，∠DCE是直角，即可得到∠BCA+∠DCE=90°+90°=180°；

（2）连接BD，AE，ON，延长BD交AE于F，先证明Rt△BCD≌Rt△ACE，得到BD=AE，∠EBD=∠CAE，则∠CAE+∠ADF=∠CBD+∠BDC=90°，即BD⊥AE，再利用三角形的中位线的性质得到ON=BD，OM=AE，ON∥BD，AE∥OM，于是有ON=OM，ON⊥OM，即△ONM为等腰直角三角形，即可得到结论；

（3）根据

（2）中证明方法，利用四边形内角和得出BD1⊥AE1，进而求出即可．

解答：

解：

（1）在一条直线上．

理由如下：

∵AB为⊙O直径，

∴∠ACB=90°，

∵△DCE为等腰直角三角形，

∴∠ACE=90°，

∴∠BCE=90°+90°=180°，

∴B、C、E三点共线．

（2）连接BD，AE，ON，

∵∠ACB=90°，∠ABC=45°，

∴BC=AC，

在△BCD和△ACE中，

∵，

∴△BCD≌△ACE，

∴AE=BD，∠DBE=∠EAC，

∴∠AEB+∠EBD=90°，

∴BD⊥AE，

∵O，N为中点，

∴ON∥BD，ON=BD，

同理：

OM∥AE，OM=AE，

∴OM⊥ON，OM=ON，

∴MN=OM，

∴=，

（3）成立．

理由如下：

连接BD1，AE1，ON1，延长BD1交AE于点F，

和

（2）一样，易证得△BCD1≌△ACE1，∴∠E1AC=∠FBC，

∠BD1C=∠AE1C，

∴∠E1FB+∠AE1C+∠D1BC+90°+∠D1CB=360°（四边形内角和定理），

又∵∠AE1C+∠D1BC+∠D1CB=180°，

∴∠E1FB+90°+180°=360°，

∴∠E1FB=90°，

∴BD1⊥AE1，

可得△ON1M1为等腰直角三角形，

从而有M1N1=OM1．

故答案为：

．

点评：

此题考查了直径所对的圆周角为直角和三角形中位线的性质；也考查了三角形全等的判定与性质、等腰直角三角形的性质以及旋转的性质．

3．如图1，在平面直角坐标系中，半径为4的⊙O交坐标轴于A、B、C、D，点P为BC上一个动点（不与B、C点重合）．连AP、BC交于点G，连FG交OB于点E．

（1）请运用圆的定义证明C、F、P、G在同一个圆上；

（2）当P为BC的中点时，求点G的坐标；

（3）如图2，连接PD，设△PAB的内切圆半径为r，求证：

．

考点：

圆的综合题．1125860

分析：

（1）取FG的中点M，连CM，PM，利用直角三角形斜边上的中线等于斜边的一半，证明CM=GM=PM=FM即可；

（2）如图1，连PC．由三角形垂心的定义推知FE⊥AB．首先由全等三角形（△ACG≌△AEG）的性质知对应边AC=AE=4；然后根据圆心角、弧、弦间的关系，勾股定理，等腰三角形的判定与性质求得BE=EG=8﹣4．则易求点G的坐标；

（3）如图2，作∠ABP的角平分线BQ交PD于点Q，过点Q作QM⊥AP，QN⊥BP，垂足分别为点M、N．通过圆周角定理，圆周角、弧、弦间的关系推知点Q即为△APB的内心．根据内心的定义以及正方形的判定推知四边形MQNP为正方形，易得PQ=QM=r；然后根据△BPQ的外交定理，等腰三角形的判定求得DQ=DB=4，所以PD=PQ+QD=r+4=（4+r）．

解答：

解：

（1）如图1，取FG的中点M，连CM，PM．

∵AB是⊙O的直径，

∴∠ACB=∠APB=90°，

∴∠BCF=∠FPB=90°

∴CM=GM=PM=FM=EG，即点C、F、P、G到点M的距离相等，

根据圆的定义：

圆是到定点的距离等于定长的点的集合．

点C、F、P、G在以点M为圆心，MC长为半径的圆上．

（2）如图1，连PC．

∵点P为弧BC的中点，

∴=，

∴∠BAP=∠CAP．

又∵AP⊥BF，BC⊥AF，AP、BC交于点G，

∴点G为△ABF的垂心，

∴FG⊥AB，即GE⊥AB．

∵在△ACG和△AEG中，

，

∴△ACG≌△AEG（AAS）．

∴AC=AE．

∵AO⊥OC，AO=OC=4，

∴AC=4，

∴AE=4．

∴OE=AE﹣AO=4﹣4，

∴BE=OB﹣OE=8﹣4．

∵∠1=∠CAB=45°，

∴∠=∠2=45°，

∴EG=BE=8﹣4，

∴点G的坐标是：

（4﹣4，8﹣4）；

（3）证明：

如图2，作∠ABP的角平分线BQ交PD于点Q，过点Q作QM⊥AP，QN⊥BP，垂足分别为点M、N．

∵=，

∴∠1=∠2=45°．

又∵BQ平分∠ABP，

∴点Q即为△PAB的内心，

∴QM=QN=r，又∠QMP=∠QNP=∠MPN=90°，

∴四边形MQ