浙江省历年高考立体几何大题总汇题目与答案.docx

浙江省历年高考立体几何大题总汇题目与答案.docx

《浙江省历年高考立体几何大题总汇题目与答案.docx》由会员分享，可在线阅读，更多相关《浙江省历年高考立体几何大题总汇题目与答案.docx（26页珍藏版）》请在冰豆网上搜索。

浙江省历年高考立体几何大题总汇题目与答案

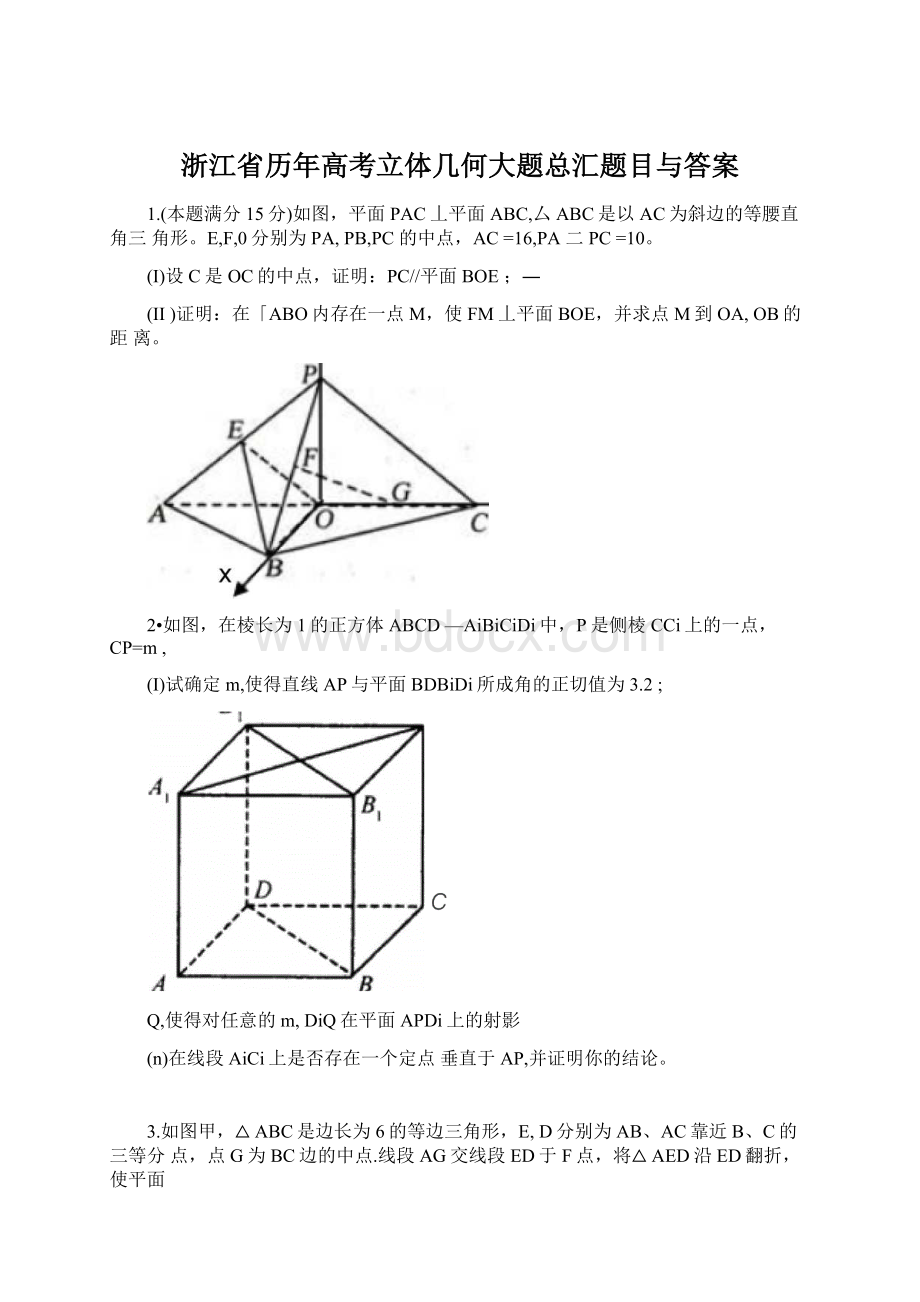
1.（本题满分15分）如图，平面PAC丄平面ABC,厶ABC是以AC为斜边的等腰直角三角形。

E,F,0分别为PA,PB,PC的中点，AC=16,PA二PC=10。

（I）设C是OC的中点，证明：

PC//平面BOE；―

（II）证明：

在「ABO内存在一点M，使FM丄平面BOE，并求点M到OA,OB的距离。

2•如图，在棱长为1的正方体ABCD—AiBiCiDi中，P是侧棱CCi上的一点，CP=m,

（I）试确定m,使得直线AP与平面BDBiDi所成角的正切值为3.2;

Q,使得对任意的m,DiQ在平面APDi上的射影

（n）在线段AiCi上是否存在一个定点垂直于AP,并证明你的结论。

3.如图甲，△ABC是边长为6的等边三角形，E,D分别为AB、AC靠近B、C的三等分点，点G为BC边的中点.线段AG交线段ED于F点，将△AED沿ED翻折，使平面

AED丄平面BCDE，连接AB、AC、AG形成如图乙所示的几何体。

（I）求证BC丄平面AFG;

（II）求二面角B—AE—D的余弦值.

5•如图，矩形ABCD和梯形BEFC所在平面互相垂直，BE//CF

BCF"CEF=90；,ADY3,EF=2.

（I）求证：

AE//平面DCF;

（n）当AB的长为何值时，二面角A-EF-C的大小为60?

2

6.如图，在矩形ABCD中，点E,F分别在线段AB,AD上,AE=EB=AF=—FD=4.沿直

3

线EF将AEF翻折成A'EF,使平面A'EF_平面BEF.

（I）求二面角A'-FD-C的余弦值;

与A'重合，求线段FM的长.

向上翻折，使C

（II）点M,N分别在线段FD,BC上，若沿直线MN将四边形MNCD

7.如图，在三棱锥P-ABC中，AB=AC,D为BC的中点，P0丄平面ABC，垂足O落在

线段AD上，已知BC=8,P0=4,AO=3,OD=2

（I）证明：

AP丄BC;

（n）在线段AP上是否存在点M,使得二面角A-MC-B为直二面角？

若存在，求出AM

的长；若不存在，请说明理由。

8.如图，在四棱锥P-ABCD中，底面是边长为2.3的菱形，

/BAD=120。

，且PA丄平面ABCD,PA=2.6,M,N分别为PB,PD的中点。

（1）证明：

MN//平面ABCD;

（2）过点A作AQ丄PC,垂足为点Q,求二面角A-MN-Q的平面角的余弦值。

点，点Q在线段AC上，且AQ=3QC.

9.如图，在四面体A-BCD中，AD_平面BCD,

BC_CD,AD=2,BD=2、、2.M是AD的中点，P是BM的中

（I）证明：

PQ//平面BCD;

（n）若二面角C-BM-D的大小为60，求.BDC的大小.

10.如图，在五面体ABCDEF中，已知DE_平面ABCD，AD//BC,•BAD=60°，

AB=2，DE二EF=1.

（1）求证：

BC//EF;

（2）求三棱锥B-DEF的体积.

B

（第16题图）

（1）求异面直线BA与CR夹角的余弦值；

（2）求二面角B—ABi—C平面角的余弦值.

12（本小题14分）在等腰梯形ABCD中，AD//BC,AD^^BC,ABC=60‘丿,N是BC

2

的中点•将梯形ABCD绕AB旋转90'；，得到梯形ABCD（如图）.

（1）求证：

AC_平面ABC;

（2）求证：

CN//平面ADD';

（3）求二面角A-CN-C的余弦值.

13.（本题满分14分）如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD//BC,

/ADC=90°,平面FAD丄底面ABCD,Q为AD的中点，M是棱PC上

A

的点，FA=PD=2,BC=丄AD=1,CD=、3.

2

（I）求证：

平面PQB丄平面PAD;

（II）若二面角M-BQ-C为30°设PM=tMC,

试确定t的值

14.如图，直角梯形ABCD中，AB//CD,.BCD=90°,BC=CD=2,AD=

BDEC丄底面ABDFD丄底面AO且有E=D=.

（I）求证：

AD丄BF:

（II）若线段EC上一点M在平面BDF上的射影恰好是BF的中点N,试求二面角B-MF-C

的余弦值•

1•证明：

（I）如图，连结0P，以0为坐标原点，分别以OB、OC、OP所在直线为x轴，y轴，z轴，建立空间直角坐标系O-xyz，-一

则O0,0,0,A（0,七,0）,B（8,0,0）,C（0,8,0）,P（0,0,6）,E（0,-4,3）,F4,0,3，由题意得,

G0,4,0,因OB=（8,0,0）,OE=（0,-4,3），因此平面BOE的法向

量为n=（0,3,4），FG=（-4,4,-3得nFG=0，又直线FG不在

（II）设点M的坐标为X0,y°,0，则FM=（Xc-4,y。

，-3），因为

FM_平面BOE，所以有FM〃n，因此有xg=4,y°--9，即点

4

M的坐标为4,-9,0L在平面直角坐标系xoy中，MOB的内部区域满足不等式组

<4丿

x0

*yV0，经检验，点M的坐标满足上述不等式组，所以在MBO内存在一点M，使

&_y£8

9

FM_平面BOE，由点M的坐标得点M到OA，OB的距离为4,一.—

4

2.解法1：

（1）连AC,设ACp|BD=O,

AP与面BDDBi交于点G,连OG.

因为PCII面BDDiBi,面BDDiBiPl面APC=OG,

1m

故OG//PC。

所以OGPC-o

22

又AO_DB,AO_BB,所以AO_面BDDiBi.

故.AGO即为AP与面BDD1B1所成的角。

在Rt△AOG中，tanAGO23、2，即m

m3

2

A

故当m=-时，直线AP与平面BDDB所成的角的正切值为3^/2o

3

（n）依题意，要在A,Ci上找一点Q，使得DiQ_AP.

可推测AiCi的中点Oi即为所求的Q点。

因为DiOi_AG.DiOi_AA，所以DiQ_面ACCiAi.

又AP面ACC,a,•，故D,。

_APo

从而DiOi在平面AD,P上的射影与AP垂直。

解法二：

（1）建立如图所示的空间直角坐标系，则

A（1,0,0）,B（1,1,0）,P（0,1,m）,C（0,1,0）,D（0,0,0）,Bi（1,1,1）,Di（0,0,1）.

TT

所以BD=（-1,-1,0）,BB,=（0,0,1）,

又由ACB^=0,Acbb：

=o知AC为平面bbd,d的一个法向量

设AP与面BDDiBi所成的角为「

则S^=COS（2-^=F|APriACC|-|=-22m2

故当m=l时，直线AP与平面BDDB所成的角的正切值为30。

3

（2）若在A|G上存在这样的点Q，设此点的横坐标为x,则Q（x,1—x,1）,DQ=（x,1—x,0）。

AP。

等价于

依题意，对任意的m要使D1Q在平面APD1上的射影垂直于

即Q为A1C1的中点时，满足题设的要求

3.（I）在图甲中，由△ABC是等边三角形，E,D分别为AB,AC的三等分点，点G为BC

边的中点，易知DE丄AF,DE丄GF,DE//BC.2分

在图乙中，因为DE丄AF,DE丄GF,AFFG=F，所以DE丄平面AFG.

又DE//BC，所以BC丄平面AFG.4分

（H）因为平面AED丄平面BCDE，平面AED平面BCDE=DE,DE丄AF,DE丄GF,

所以FA,FD,FG两两垂直.

以点F为坐标原点，分别以FG,FD,FA所在的直线为x,y,Z轴，建立如图所示

的空间直角坐标系F-xyz.则A（0,0,2.3）,B（,3厂3,0）,E（0,-2,0），所以

AB=（、3,-3,-2、3）,BE=（-..3,1,0）.设平面ABE的一个法向量为n二（x,y,z）.ntR.AB=0刚fV3x_3y_2l‘3z=0则＜，即丿厂,

n，BE=0厂J3x+y=0

取x=1，则y=.3,z=-1，则n=（1,3,-1）.

显然m=（1,0,0）为平面ADE的一个法向量,

4.方法一：

（1）证明：

因为AC=BCM是AB的中点，所以CMLAB.又EA丄平面ABC,所以CMLEM

（2）解：

过点M作MHL平面CDE垂足是H,连结CH并延长交ED于点F,连结MF、MD/FCM是直线CM

和平面CDE所成的角.

因为MHL平面CDE所以MHLED,又因为CML平面EDM所以CMLED,则EDL平面CMF因此EDLMF

设EA=a,BD=BC=AC=2a,

在直角梯形ABDE中,AB=2、、2a,M是AB的中点,

所以DE=3a,EM=、、3a,MD=、、6a,得厶EMD是直角三角形，其中/EMD=90°

EMMD—所以MF=2a.

DE

MF

在Rt△CMF中，tan/fcm=mc=1，所以/FCM=45,可得四边形BCGE为矩形,又ABCD为矩形，

故EM_CM.

（2）解：

设向量n=（1,yo,x0）与平面CDE垂直,

即n-CE=0,n-CD=0.

因为CE=（2a,0,a）,CD=（0,2a,2a）,

所以y0=2，z0=-2，

即n=（1,2,-2）,十

nCMCMh逅

coscn,CM>=—

M」n

直线CM与平面CDE所称的角是45°.

5.方法一：

（I）证明：

过点E作EG_CF交CF于G，连结DG,

E

所以AD丄EG，从而四边形ADGE为平行四边形，

故AE//DG•

因为AE二平面DCF,DG二平面DCF,

所以AE//平面DCF•

（n）解：

过点B作BH_EF交FE的延长线于H，连结AH•

由平面ABCD_平面BEFC,AB_BC，得

AB_平面BEFC,

从而AH_EF•

所以.AHB为二面角A-EF-C的平面角.

在Rt△EFG中，因为EG=AD=,3,EF=2，所以.CFE=60：

FG=1.

空间直角坐标系C-xyz•设AB二a,BE二b,CF二c,

则C（0,0,0）,AC、3,0,a）,B（、、3,0,0）,E（、3,b,0）,F（0,c,0）•

（I）证明：

AE=（0,b,a）,CB=（E,0,0）,BE=（0,b,0）,

所以

CB_CE=0,

c^Lbe

=0,从而CB_AE,CB_BE,

所以CB_平面ABE