全国中考数学试题分类解析汇编专题网格问题.doc

全国中考数学试题分类解析汇编专题网格问题.doc

《全国中考数学试题分类解析汇编专题网格问题.doc》由会员分享，可在线阅读，更多相关《全国中考数学试题分类解析汇编专题网格问题.doc（26页珍藏版）》请在冰豆网上搜索。

郑州郭氏数学内部资料；更多学习资料及学习方法、考试技巧请百度郭氏数学公益教学博客。

2013年全国中考数学试题分类解析汇编

专题33：

网格问题

一、选择题

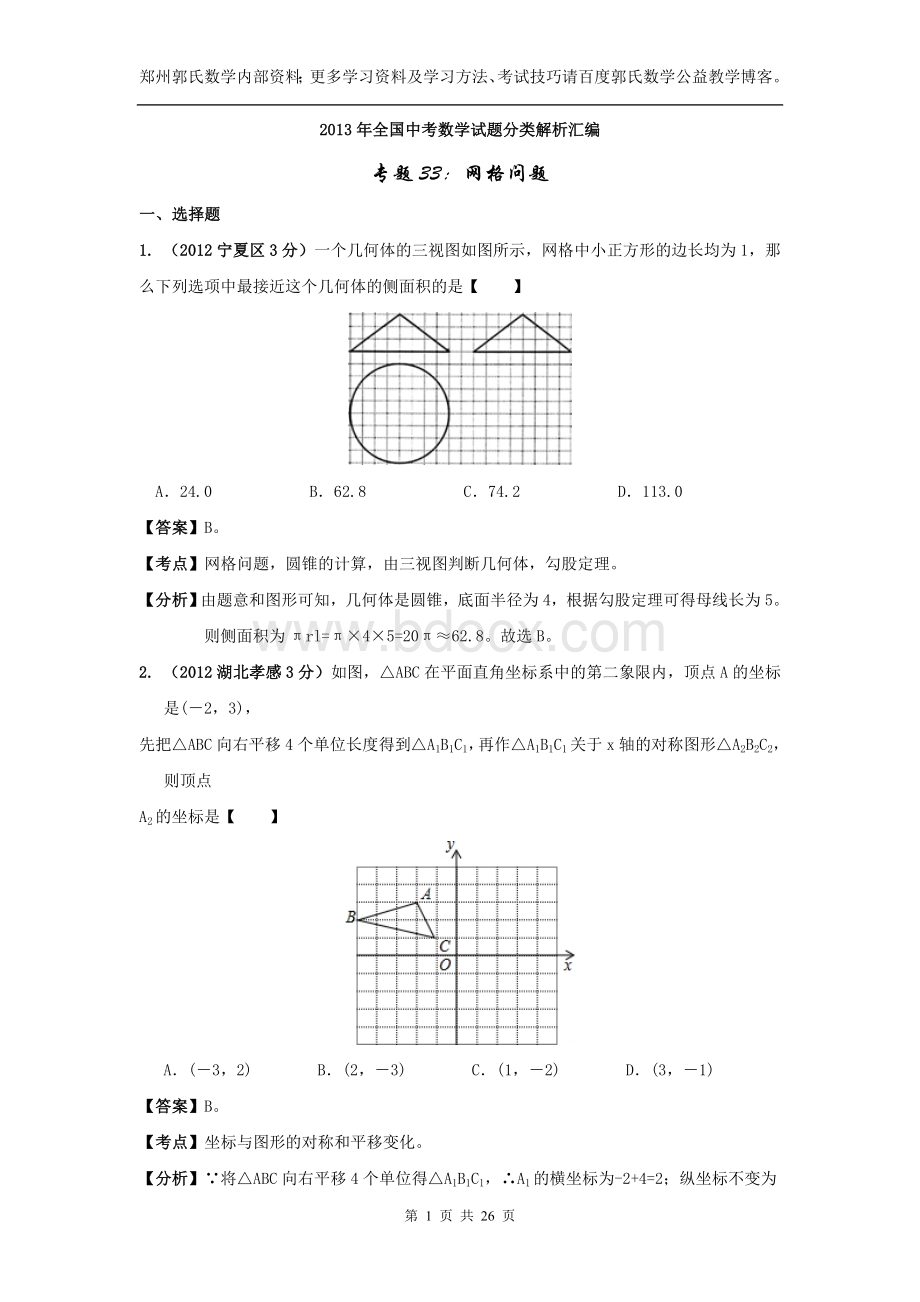
1.（2012宁夏区3分）一个几何体的三视图如图所示，网格中小正方形的边长均为1，那么下列选项中最接近这个几何体的侧面积的是【】

A．24.0B．62.8C．74.2D．113.0

【答案】B。

【考点】网格问题，圆锥的计算，由三视图判断几何体，勾股定理。

【分析】由题意和图形可知，几何体是圆锥，底面半径为4，根据勾股定理可得母线长为5。

则侧面积为πrl=π×4×5=20π≈62.8。

故选B。

2.（2012湖北孝感3分）如图，△ABC在平面直角坐标系中的第二象限内，顶点A的坐标是（－2，3），

先把△ABC向右平移4个单位长度得到△A1B1C1，再作△A1B1C1关于x轴的对称图形△A2B2C2，则顶点

A2的坐标是【】

A．（－3，2）B．（2，－3）C．（1，－2）D．（3，－1）

【答案】B。

【考点】坐标与图形的对称和平移变化。

【分析】∵将△ABC向右平移4个单位得△A1B1C1，∴A1的横坐标为-2+4=2；纵坐标不变为3；

∵把△A1B1C1以x轴为对称轴作轴对称图形△A2B2C2，∴A2的横坐标为2，纵坐标为－3。

∴点A2的坐标是（2，－3）。

故选B。

3.（2012湖北荆门3分）下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是【】

A．B．C．D．

4.（2012山东聊城3分）如图，在方格纸中，△ABC经过变换得到△DEF，正确的变换是【】

A．把△ABC绕点C逆时针方向旋转90°，再向下平移2格　　

B．把△ABC绕点C顺时针方向旋转90°，再向下平移5格　　

C．把△ABC向下平移4格，再绕点C逆时针方向旋转180°　　

D．把△ABC向下平移5格，再绕点C顺时针方向旋转180°

【答案】B。

【考点】几何变换的类型。

【分析】根据图象，△ABC绕点C顺时针方向旋转90°，再向下平移5格即可与△DEF重合。

故选B。

二、填空题

1.（2012天津市3分）“三等分任意角”是数学史上一个著名问题已知一个角∠MAN设

（Ⅰ）当∠MAN=690时，的大小为▲（度）；

（Ⅱ）如图，将∠MAN放置在每个小正方形的边长为1cm的网格中，角的一边AM与水平方向的网格线平行，另一边AN经过格点B，且AB=2.5cm．现要求只能使用带刻度的直尺，请你在图中作出，并简要说明作法（不要求证明）▲．

【答案】（Ⅰ）23。

（Ⅱ）如图，让直尺有刻度一边过点A，设该边与过点B的竖直方向的网格线交于点C，与过点B水平方向的网格线交于点D，保持直尺有刻度的一边过点A，调整点C、D的位置，使CD=5cm，画射线AD，此时∠MAD即为所求的∠α。

【考点】作图（应用与设计作图），直角三角形斜边上的中线性质，三角形的外角性质，平行的性质。

【分析】（Ⅰ）根据题意，用69°乘以，计算即可得解：

×69°=23°。

（Ⅱ）利用网格结构，作以点B为直角顶点的直角三角形，并且使斜边所在的直线过点A，且斜边的长度为5，根据直角三角形斜边上的中线等于斜边的一半可得斜边上的中线等于AB的长度，再结合三角形的外角性质可知，∠BAD=2∠BDC，再根据两直线平行，内错角相等可得∠BDC=∠MAD，从而得到∠MAD=∠MAN。

2.（2012浙江杭州4分）如图，平面直角坐标系中有四个点，它们的横纵坐标均为整数．若在此平面直角坐标系内移动点A，使得这四个点构成的四边形是轴对称图形，并且点A的横坐标仍是整数，则移动后点A的坐标为▲．

【答案】（﹣1，1），（﹣2，﹣2）。

【考点】利用轴对称设计图案。

【分析】根据轴对称图形的定义：

如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，把A进行移动可得到点的坐标：

如图所示：

A′（﹣1，1），A″（﹣2，﹣2）。

3.（2012江苏泰州3分）如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这

些小正方形的顶点上，AB、CD相交于点P，则tan∠APD的值是▲．

【答案】2。

【考点】正方形的性质，相似三角形的判定和性质，锐角三角函数的定义。

【分析】如图，连接BE，交CD于点F。

∵四边形BCED是正方形，

∴DF=CF=CD，BF=BE，CD=BE，BE⊥CD，∴BF=CF。

根据题意得：

AC∥BD，∴△ACP∽△BDP。

∴DP：

CP=BD：

AC=1：

3。

∴DP=PF=CF=BF。

在Rt△PBF中，。

∵∠APD=∠BPF，∴tan∠APD=2。

三、解答题

1.（2012安徽省8分）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点A1.

（1）画出一个格点△A1B1C1，并使它与△ABC全等且A与A1是对应点；

（2）画出点B关于直线AC的对称点D，并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.

【答案】解：

（1）答案不唯一，如图，平移即可：

（2）作图如上，

∵AB=，AD=，BD=，∴AB2+AD2=BD2。

∴△ABD是直角三角形。

∴AD可以看作由AB绕A点逆时针旋转90°得到的。

【考点】作图（平移变换、轴对称变换），全等图形，旋转和轴对称的性质，勾股定理和逆定理。

【分析】

（1）利用△ABC三边长度，画出以A1为顶点的三角形三边长度即可，利用图象平移，可得出

△A1B1C1。

（2）利用点B关于直线AC的对称点D，得出D点坐标，根据勾股定理和逆定理可得出AD与AB的位置关系。

2.（2012海南省8分）如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（－2，4）、（－2，0）、（－4，1），结合所给的平面直角坐标系解答下列问题：

（1）画出△ABC关于原点O对称的△A1B1C1.

（2）平移△ABC，使点A移动到点A2（0，2），画出平移后的△A2B2C2并写出点B2、C2的坐标.

（3）在△ABC、△A1B1C1、△A2B2C2中，△A2B2C2与成中心对称，其对称中心的坐标为.

【答案】解：

（1）△ABC关于原点O对称的△A1B1C1如图所示：

（2）平移后的△A2B2C2如图所示：

点B2、C2的坐标分别为（0，－2），（－2，－1）。

（3）△A1B1C1；（1，－1）。

【考点】网格问题，作图（中心对称变换和平移变换），中心对称和平移的性质。

【分析】

（1）根据中心对称的性质，作出A、B、C三点关于原点的对称点A1、B1、C1，连接即可。

（2）根据平移的性质，点A（－2，4）→A2（0，2），横坐标加2，纵坐标减2，所以将B（－2，0）、C（－4，1）横坐标加2，纵坐标减2得到B2（0，－2）、C2（－2，－1），连接即可。

（3）如图所示。

3.（2012广东梅州7分）如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A1OB1．（直接填写答案）

（1）点A关于点O中心对称的点的坐标为　　；

（2）点A1的坐标为　　；

（3）在旋转过程中，点B经过的路径为弧BB1，那么弧BB1的长为　　．

【答案】解：

（1）（﹣3，﹣2）。

（2）（﹣2，3）。

（3）。

【考点】坐标与图形的旋转变化，关于原点对称的点的坐标特征，弧长的计算。

【分析】

（1）根据关于坐标原点成中心对称的点的横坐标与纵坐标都互为相反数的性质即可得。

（2）根据平面直角坐标系写出即可。

（3）先利用勾股定理求出OB的长度，然后根据弧长公式列式进行计算即可得解：

根据勾股定理，得，∴弧BB1的长=。

4.（2012广东广州12分）如图，⊙P的圆心为P（﹣3，2），半径为3，直线MN过点M（5，0）且平行于y轴，点N在点M的上方．

（1）在图中作出⊙P关于y轴对称的⊙P′．根据作图直接写出⊙P′与直线MN的位置关系．

（2）若点N在

（1）中的⊙P′上，求PN的长．

【答案】解：

（1）如图所示，⊙P′即为所求作的圆。

⊙P′与直线MN相交。

（2）设直线PP′与MN相交于点A，

则由⊙P的圆心为P（﹣3，2），半径为3，直线MN过点M（5，0）且平行于y轴，点N在⊙P′上，得

P′N=3，AP′=2，PA=8。

∴在Rt△AP′N中，

。

在Rt△APN中，。

【考点】网格问题，作图（轴对称变换），直线与圆的位置关系，勾股定理。

【分析】

（1）根据关于y轴对称的点的横坐标互为相反数，纵坐标相等找出点P′的位置，然后以3为半径画圆即可。

再根据直线与圆的位置关系解答。

（2）设直线PP′与MN相交于点A，在Rt△AP′N中，利用勾股定理求出AN的长度，在Rt△APN中，利用勾股定理列式计算即可求出PN的长度。

5.（2012浙江温州8分）如图，在方格纸中，△PQR的三个顶点及A,B,C,D,E五个点都在小方格的顶点上，现以A,B,C,D,E中的三个顶点为顶点画三角形，

（1）在图甲中画出一个三角形与△PQR全等；

（2）在图乙中画出一个三角形与△PQR面积相等但不全等.

【答案】解：

（1）如图所示：

（2）如图所示：

【考点】作图（复杂作图），全等图形。

【分析】

（1）过A作AE∥PQ，过E作EB∥PR，再顺次连接A、E、B。

（答案不唯一）

（2）∵△PQR面积是：

×QR×PQ=6，∴连接BA，BA长为3，再连接AD、BD，三角形的面积也是6，但是两个三角形不全等。

（答案不唯一）

6.（2012江苏泰州10分）如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上，将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1，然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2．

（1）在网格中画出△A1B1C1和△A1B2C2；

（2）计算线段AC在变换到A1C2的过程中扫过区域的面积（重叠部分不重复计算）

【答案】解：

（1）如图所示：

（2）∵图中是边长为1个单位长度的小正方形组成的网格，

∴。

∵将△ABC向下平移4个单位AC所扫过的面积是以4为底，以2为高的平行四边形的面积：

4×2=8。

再向右平移3个单位AC所扫过的面积是以3为底，以2为高的平行四边形的面积：

4×2=6。

当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时，A1C1所扫过的面积是以A1为圆心以以为半径，圆心角为90°的扇形的面积，重叠部分是以A1为圆心，以为半径，圆心角为45°的扇形的面积，去掉重叠部分，面积为：

∴线段AC在变换到A1C2的过程中扫过区域的面积=8＋6＋π×=14+π。

【考点】作图（平移和旋转变换），平移和旋转的性质，网格问题，勾股定理，平行四边形面积和扇形面积的计算。

【分析】

（1）根据图形平移及旋转的性质画出△A1B1C1及△A1B2C2即可。

（2）画出图形，根据图形平移及旋转的性质分三部