一次回归正交设计二次回归正交设计二次回归旋转设计Word文件下载.docx

一次回归正交设计二次回归正交设计二次回归旋转设计Word文件下载.docx

《一次回归正交设计二次回归正交设计二次回归旋转设计Word文件下载.docx》由会员分享，可在线阅读，更多相关《一次回归正交设计二次回归正交设计二次回归旋转设计Word文件下载.docx（11页珍藏版）》请在冰豆网上搜索。

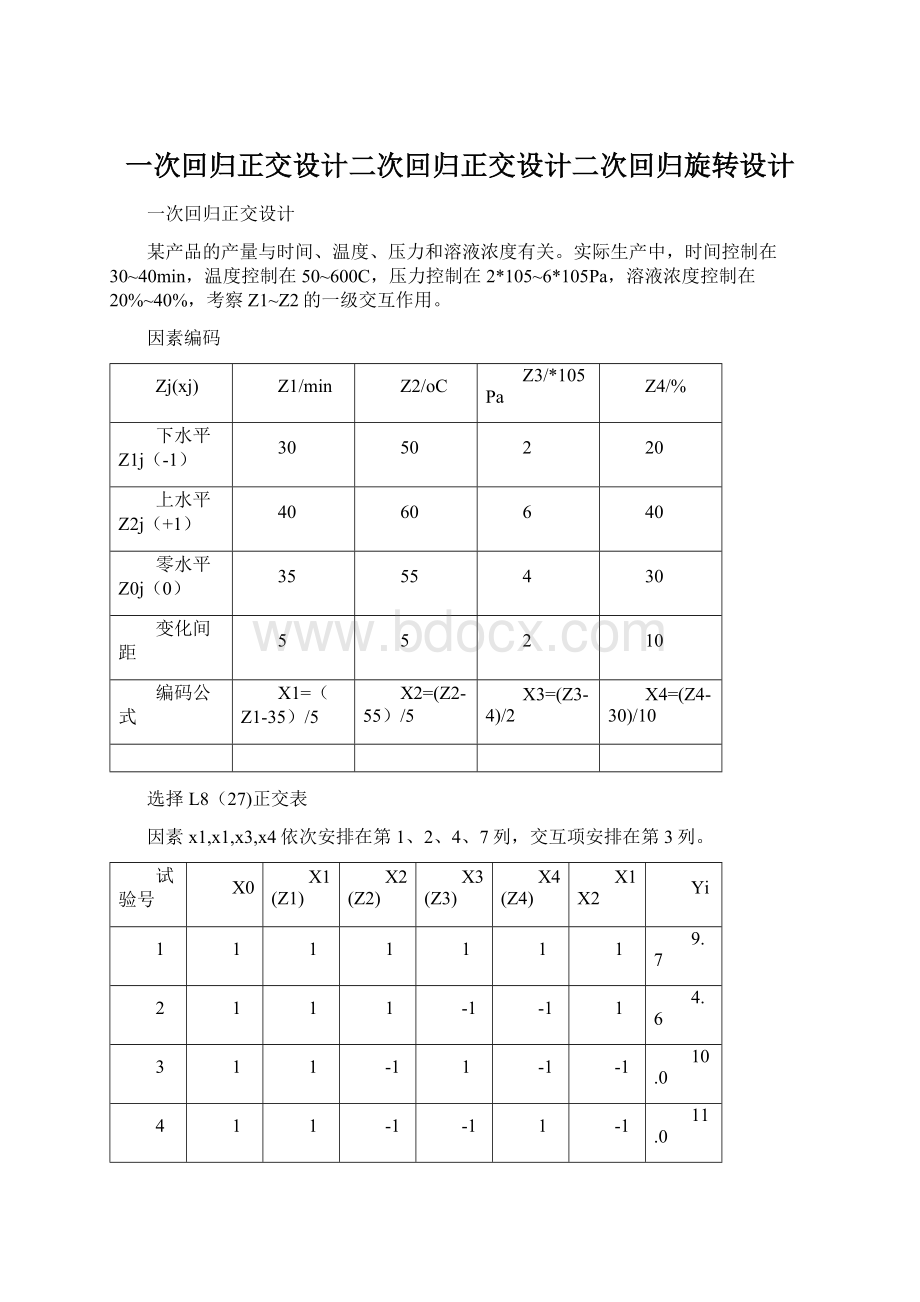
X4（Z4）

X1X2

Yi

1

9.7

-1

4.6

3

10.0

11.0

9.0

7

7.3

8

2.4

9

7.9

8.1

11

7.4

Bj=∑xjy

87.4

6.6

2.6

8.0

12.0

-16.0

aj=∑xj2

bj=Bj/aj

7.945

0.825

0.325

1.000

1.500

-2.00

Qj=Bj2/aj

393

5.445

0.845

8.000

18.000

32.000

可建立如下的回归方程。

Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2

显著性检验：

1、回归系数检验

回归关系的方差分析表

变异来源

SS平方和

Df自由度

MS均方

F

显著水平

x1

76.25

0.01

x2

11.83

0.05

x3

112.04

x4

252.10

x1x2

448.18

回归

64.29

12.858

180.08

剩余

0.357

0.0714

失拟

0.097

0.0323

0.25

<

误差e

0.26

0.13

总和

64.647

经F检验不显著的因素或交互作用直接从回归方程中剔掉，不必再重新进行回归分析。

2、回归方程的检验

进行此项检验时，通常对F值小于等于1的项不进行检验，直接从回归方程中剔除，对经检验而α>

0.25的项，根据实际需要决定是否剔除。

3、失拟检验

由回归系数的检验，回归方程的检验，失拟检验可以得出，

产量y与各因素之间的总回归关系达到显著，回归方程拟合效果较好。

回归方程的变换

将各因素的编码公式代入，得

Y=-162.05+4.57z1+2.87z2+0.50z3+0.15z4-0.08z1z2

二次回归正交设计

某食品加香试验，3个因素，即Z1（香精用量）、Z2（着香时间）、Z2（着香温度）

（1）确定γ值、mc及m0。

根据本试验目的和要求，确定mc＝2m＝23＝8，m0＝1，查表得γ＝1.215。

（2）确定因素的上、下水平，变化间距以及对因子进行编码

编码

Z1/（mL／kg物料）

Z2 

/ 

h

Z3 

℃

+γ

18

24

48

+ 

16.94

22.6

45.7

12

16

- 

7.06

9.4

24.3

-γ

22

Δi

4.94

10.7

计算各因素的零水平：

Z01＝（18＋6）/2＝12（mL/kg）

Z02＝（24＋8）/2＝16（h）

Z03＝（48＋22）/2＝35（℃）

计算各因素的变化间距：

Δ01＝（18-12）/1.215＝4.94（mL/kg）

Δ02＝（24-16）/1.215＝6.6（h）

Δ03＝（48-35）/1.215＝10.7（℃）

（3）列出试验设计及试验方案

试 

验 

设 

计

实 

施 

方 

案

x0

香精用量／（mL／kg）

着香时间／h

着香温度/ 

1.215

-1.215

13

14

15

试验结果的统计分析

建立回归方程

回归关系的显著性测验。

平方和（SS）

自由度（df）

均方（MS）

显著程度

0.63327

＜1

ns

4.85856

6.8624*

0.05（6.61）

7.70400

10.8814*

4.91410

10.3994*

x1x3

4.75861

6.9409*

x2x3

3.90601

5.5170

0.10（4.06）

x12

23.86763

33.7116**

0.01（16.30）

x22

0.06407

x32

4.44220

6.2743

55.20320

6.13369

8.6635*

0.05（4.77）

3.53998

0.70799

总变异

58.74317

方差分析表明，总回归达到显著水平，说明本食品的加香试验与所选因素之间存在显著的回归关系，试验设计方案是正确的，选用二次正交回归组合设计也是恰当的。

除x1和x22以外，其余各项因子基本达到显著或极显著，说明香料用量、着香时间、着香温度与这一食品的加香有显著或极显著关系。

本试验设计的因素、水平选择是成功的。

在这种回归正交试验中，第一次方差分析往往因为误差（剩余）自由度偏小而影响了检验的精确度。

并且由于回归正交试验计划具有的正交性，保证了试验因素的列与列之间没有互作（即没有相关性）存在，因此我们可以将未达到0.25以上显著水平的因素（或者互作）剔除，将其平方和和自由度并入误差（剩余）项，进行第二次方差分析，以提高检验的精确度。

第二次方差分析结果见下表：

8.0263*

0.05（5.59）

12.7269**

0.01（12.20）

8.1180*

7.8612*

6.4527*

39.4290**

7.3385*

54.24265

7.74895

12.8012**

0.01（6.99）

4.23732

0.60533

58.47997

第二次方差分析表明，总回归及各项因素均达到显著或极显著水平，说明这一食品加香与试验因素之间存在极显著的回归关系，其优化的回归方程为：

本试验由于m0＝1，故不能进行失拟检验，这是试验的一个缺陷。

如果取m0＝4，对试验进行失拟检验，则本试验将更为圆满。

二次回归旋转设计

对乳酸发酵的产酸条件进行优化试验，采用二次回归旋转设计对盐浓度、糖浓度、发酵温度和发酵时间进行试验。

因素水平表

盐浓度 

糖浓度 

发酵温度 

发酵时间 

/%

/℃

/h

+2

6.0

37.0

+1

7.0

5.0

34.0

44

4.0

31.0

3.0

28.0

36

-2

2.0

25.0

设计方案及结果

处理号

含酸量 

yα 

%

0.654

0.433

0.538

0.321

0.314

0.279

0.295

0.242

0.779

0.594

0.710

0.529

0.481

0.307

0.328

0.291

17

0.125

0.648

19

0.785

0.213

21

0.429

0.198

23

0.842

0.486

25

0.797

26

0.709

27

0.759

28

0.694

29

0.728

0.738

31

0.746

根据计算

建立回归方程

回归方程的显著性检验

变异原因

平方和SS

自由度df

均方MS

F值

0.16484

49.28

8.53

0.41738

127.79

0.04585

13.71

0.13726

41.04

x1 

0.00946

2.83

0.00002

0.00016

x2 

0.00117

0.01594

4.77

4.49

x3 

0.00101

x1′

0.16884

50.48

x2′

0.07959

23.79

x3′

0.34411

102.88

x4′

0.01648

4.93

1.40211

0.10015

29.94

3.56

0.05352

0.00334

误差

0.00853

0.00142

0.04499

0.00450

3.17

4.74

1.45563

通过回归方程检验，回归系数检验，失拟检验，可以看出，回归达到极显著水平。

说明本试验设计及分析效果都很好，各因素间显著与不显著也很分明。

因此没有必要做二次回归方差分析，可直接将F＜1的回归系数去掉而得到含酸量与各因素间的回归方程为：