中考数学平面几何经典题文档格式.docx

中考数学平面几何经典题文档格式.docx

《中考数学平面几何经典题文档格式.docx》由会员分享，可在线阅读，更多相关《中考数学平面几何经典题文档格式.docx（10页珍藏版）》请在冰豆网上搜索。

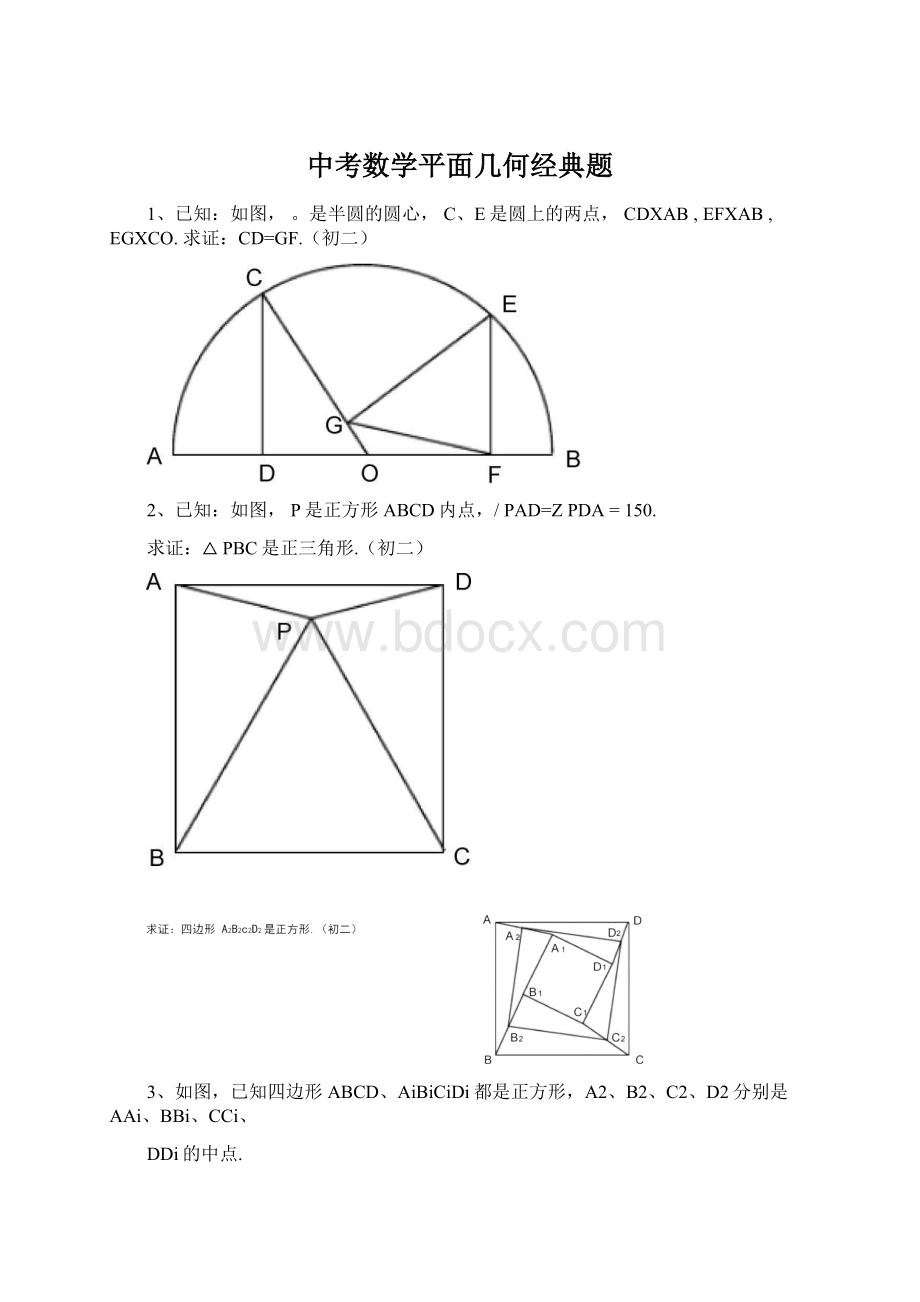
（1）求证：

AH=2OM;

（2）若/BAC=600,求证：

AH=AO.（初二）

2、设MN是圆。

外一直线，过。

作OALMN于A,自A引圆的两条直线，交圆于B、C及

D、E,直线EB及CD分别交MN于P、Q.求证：

AP=AQ.（初二）

3、如果上题把直线MN由圆外平移至圆内，则由此可得以下命题:

设MN是圆O的弦，过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于

Q.

AP=AQ.（初二）

4、如图，分别以△ABC的AC和BC为一边，在△ABC的外侧作正方形ACDE和正方形CBFG,

点P是EF的中点.

点P到边AB的距离等于AB的一半

DE//AC,AE=AC,AE与CD相交于F.

1、如图，四边形ABCD为正方形,求证：

CE=CF.（初二）

3、设P是正方形ABCD一边BC上的任一点，PFXAP,求证：

PA=PF.（初二）

2、设P是平行四边形ABCD内部的一点，且/求证：

/PAB=/PCB.（初二）

3、设ABCD为圆内接凸四边形，求证：

AB-CD+AD-BC=AC-BD.（初三）

4、平行四边形ABCD中，设E、F分别是BC、AB上的一点，AE与CF相交于P,且AE=CF.求证：

/DPA=/DPC.（初二）

1、设P是边长为1的正△ABC

P是边长为1的止方形ABCD内E

3、P为止方形ABCD内的一点，并且PA=

4、如图，△ABC中，/ABC=/ACB=80

内任一点，L=PA+PB+PC,求证：

A

-A-BC

<

L<

2.

内一点，求PA+PB+PC的最小值.ArD

BC

a,PB=2a,PC=3a,求止方形的边长.

AcD

L

°

D、E分别是AB、AC上的点，/DCA=30°

C

/EBA=200,求/BED的度数.

1.如下图做GHLAB,连接EO。

由于GOFE四点共圆，所以/GFH=/OEG,即△GHFs^OGE,可得~^^==，又CO=EO,所以CD=GF得证。

GFGHCD

2.如下图做^DGC使与△ADP全等，可得△PDG为等边△,从而可得

△DGC^AAPD^ACGP彳导出PC=AD=DC,和/DCG=/PCG=150所以/DCP=300,从而得出^PBC是正三角形

3.如下图连接BC和AB分别找其中点F,E.连接QF与AE并延长相交于Q点,连接EB并延长交GQ于H点，连接FB并延长交AQ于G点，

由AE=2AiB=；

BC=FB2,EB=；

AB=2bC=FCi,又/GFQ+/Q=900和

/GEB2+/Q=900，所以/GEB=/GFQ又/B2FC2=/A2EB2,

可得△B2FC2^AA2EB2,所以A2B2=B2c2,

又/GFQ+/HB2F=900和/GFQ=/EB2A2,

从而可得/A2B2C2=900,

同理可得其他边垂直且相等，

从而得出四边形A2B2c2D2是正方形。

4.如下图连接AC并取其中点Q,连接QNfflQM所以可得/QMF=/F,/QNM=/DEN和/QMN=ZQNM,从而得出/DEN=/F。

1.

（1）延长AC®

F连BF,彳OOG.AF,

又/F=ZACB=/BHD,

可彳导BH=BF,从而可得HD=DF,

又AH=GF+HG=GH+HD+DF+HG=2（GH+HD）=2OM

（2）连接OBOC既得/BOC=1200,

从而可得/BOM=600,

所以可得OB=2OM=AH=AO,

得证。

3.作OHCDOG_BE,连接OP,OA,OF,AF,OG,AG,OQ。

…AD-AC-CD-2FD-FD

由于————，

AB-AE-BE-2BG.BG

由此可得^ADF^AABG,从而可得/AFC=/AGE。

又因为PFOA与QGOA四点共圆，可得/AFC=/AOP和/AGE=/AOQ,/AOP=/AOQ,从而可得AP=AQ。

4.过E,C,F点分别作AB所在直线的高EGCI,FH可得PQ=EG-FH

2

由^EGA^AAIC,可得EG=AI,由^BFH^ACBI,可得FH=BI。

AI-BIAB

从而可得PQ==—,从而信证。

22

1.顺时针旋转^ADE,到^ABG,连接CG

由于/ABG=/ADE=900+450=1350

从而可得B,G,D在一条直线上，可得△AGB^ACGBo

推出AE=AG=AC=GC,可得△AGC为等边三角形。

ZAGB=300,既得/EAC=300,从而可得/AEC=750。

又/EFC=/DFA=450+300=750.

可证：

CE=CF。

2.连接BD作CKDE,可得四边形CGDH是正方形。

由AC=CE=2GC=2CH,

可得/CEH=30°

所以/CAE=ZCEA=ZAED=15°

又/FAE=90°

+45°

+15°

=150°

从而可知道/F=15。

，从而得出AE=AFo

3.作FGLCQF&

BE,可以得出GFEC为正方形。

令AB=Y,BP=X,CE=Z,可得PC=Y-X。

vZ

2+XZ,

tanZBAP=tanZEPF=一=,可得YZ=XY-X

YY-X-Z

即Z（Y-X）=X（Y-X）,既得X=Z,得出△ABPW^PEF得到PA=PF,得证。

顺时针旋转^ABP600,连接PQ,则^PBQ是正三角形。

可得△PQC是直角三角形。

所以/APB=1500。

2.作过P点平行于AD的直线，并选一点E,使AE//DCBEPC.

可以得出/ABP=/ADP=/AEP,可得：

AEBP共圆（一边所对两角相等）。

可得/BAP=/BEP=/BCP,得证。

3.在BD取一点E,使/BCE=/ACD,既得△BEC^AADC,可得:

BE=殷,即AD?

BC=BE?

AC,

BCAC

又/ACB=/DCE,可得△ABCDEC,既得

ABDE

——=——,即AB?

CD=DE?

AC,

ACDC

由①+②可得：

AB?

CD+AD?

BC=AC（BE+DE尸AC-BD,得证。

S

4.过D作AQhAE,AG，CF,由S,'

，ade=-UABCD=Sdfc,可得:

ae|pQ=ae|pq^ae=fco

可得DQ=DG,可得/DPA=ZDPC（角平分线逆定理）。

1.

（1）顺时针旋转^BPC600,可得△PBE为等边三角形。

既得PA+PB+PC=AP++PE+EF要使最小只要AP,PE,EF在一条直线上,

即如下图：

可得最小L=

（2）过P点作BC的平行线交AB,AC与点D,F。

由于/APD>

ZATP=ZADP,

推出AD>

AP①

又BP+DP>

BP②

和PF+FOPC③

又DF=AF④

由①②③④可得：

最大L<

2;

wLv2。

1）和

（2）既得：

2.顺时针旋转4BPC600,可得△PBE为等边三角形。

既得PA+PB+PC=AP+PE+EF要使最小只要AP，PE，EF在一条直线上，

可得最小PA+PB+PC=AF。

V6十72

3.顺时针旋转^ABP900,可得如下图:

既得正方形边长L=（2

2-,中

5一

a。

4.在AB上找一点F,使/BCF=600

连接EF,DG,既得△BGC为等边三角形,

，推出△ABE^^ACF,

可得/AFE=800,

既得：

/DFG=400

可得/DCF=100,/FCE=200得到BE=CF,FG=GE。

推出：

△FGE为等边三角形

又BD=BC=BG既得/BGD=800,既得/DGF=400推得：

DF=DG得到：

△DFE0^DGE,

从而推得：

/FED=/BED=300