自动控制原理实验报告西南交通大学课程与资源中心文档格式.docx

自动控制原理实验报告西南交通大学课程与资源中心文档格式.docx

《自动控制原理实验报告西南交通大学课程与资源中心文档格式.docx》由会员分享，可在线阅读，更多相关《自动控制原理实验报告西南交通大学课程与资源中心文档格式.docx（24页珍藏版）》请在冰豆网上搜索。

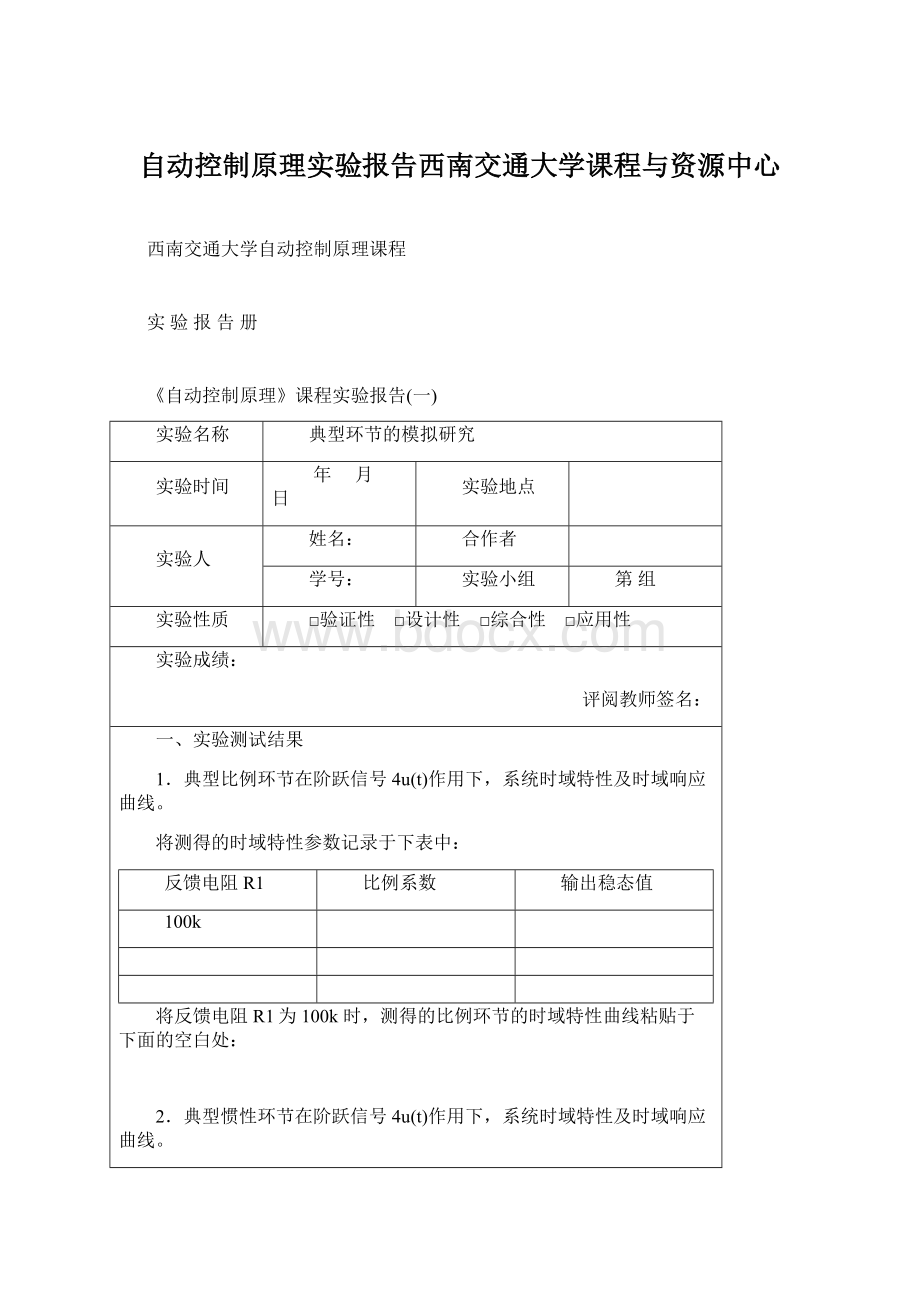
比例系数K

时间常数T

200kΩ

1F

将反馈电阻R1为200k，反馈电容C为1F时，测得的惯性环节的时域特性曲线粘贴于下面的空白处：

3．典型积分环节在阶跃信号u（t）作用下，系统时域特性及时域响应曲线。

输入电阻R0

时间常数Ti

1F

将输入电阻R0为200k，反馈电容C为1F时，测得的积分环节的时域特性曲线粘贴于下面的空白处：

4.比例积分环节在阶跃信号u（t）作用下，系统时域特性及时域响应曲线。

2F

将输入电阻R0为200kΩ，反馈电容C为2F时，测得的比例积分环节的时域特性曲线粘贴于下面的空白处：

5.比例微分环节在阶跃信号0.5u（t）作用下，系统时域特性及时域响应曲线。

ΔV

Δt

KD（T/）

微分时间常数TD（

）

将测得的比例微分环节的时域特性曲线粘贴于下面的空白处：

6.比例积分微分环节在阶跃信号0.2u（t）作用下，系统时域特性及时域响应曲线。

反馈电阻

R1

输入电压

幅值Ui

Kp

KpUi

积分时间

常数Ti

10k

将输入电阻R0为10k，反馈电阻R1为10k时，测得的比例积分微分环节的时域特性曲线粘贴于下面的空白处：

二、实验分析总结

1．从实验得到的惯性环节的阶跃响应曲线上求出K、T和调节时间Ts（

），并与理论值比较。

三、思考题

1．比例环节的输出量与输入量成比例；

积分环节的输出量是输入量的积累，具有记忆的功能；

微分环节的输出量含有输入量微分的信息。

讨论比例积分微分环节的功能。

《自动控制原理》课程实验报告

（二）

二阶系统瞬态响应和稳定性

1.积分环节参数（R1＝500k，C1=2F），惯性环节参数（R2＝100k，C2=1F），将（A11）中的直读式可变电阻R分别调整到100k、40k、10k、4k和2k，分别观察系统在阶跃信号2u（t）作用下的响应曲线，

（1）将测得的时域性能指标填入下表：

参数

项目

输入电阻

R（A3）

增益

K

自然频率

n

（计算值）

阻尼比

超调量

P.O.

峰值时间

TP

调节时间

TS（5%）

测量值

计算值

>

1

过阻尼

100k

=1

临界阻尼

40k

0<

<

欠阻尼

10k

4k

2k

（2）将电阻R分别取为4k、40k和100k时，系统在2u（t）作用下的响应曲线粘贴于下面的空白处：

2.改变积分环节参数（R1=100k，其余不变：

C1=2F），惯性环节（R取为4k，其余参数不变：

C2=1F，R2＝100k），重新观测结果，记录超调量P.O.、峰值时间Tp和调节时间Ts，填入下表。

（计算值实验前必须按公式计算出）

K

3.积分环节参数同１（R1＝500k，C1=2F），惯性环节参数（C2改变为2F，其余不变：

R2＝100k，R＝4k），重新观测结果，记录超调量、峰值时间和调节时间，填入下表。

1．根据实验结果，讨论二阶系统参数（、n）变化对系统性能的影响。

1．对于二阶系统，若将其反馈接成了正反馈，或将反馈回路断开，这时的阶跃响应有何特点？

《自动控制原理》课程实验报告（三）

三阶系统瞬态响应和稳定性

1.积分环节（A2单元）参数（R1=500k，C1=2F），惯性环节（A3单元）参数（R2=R3=100K，C2=1F），惯性环节（A5单元）参数（R4=500K，C3=1F），惯性环节（A5单元）输入电阻R调整到30k、41.7k、100k，分别观察系统在阶跃信号2u（t）作用下的响应曲线，并将响应曲线粘贴于下面的空白处：

2.改变时间常数（分别改变运算模拟单元A3和A5的反馈电容C2、C3），重新观测结果，将临界稳定时的测量值和计算值填入下表。

反馈电容C2

（A3）

反馈电容C3（A5）

临界稳定（等幅振荡）时，A5单元的输入电阻R

（A11阻容元件库中的可变电阻）

2F

《自动控制原理》课程实验报告（四）

线性控制系统根轨迹分析

1．用MATLAB绘制原系统根轨迹图，观测原系统在单位阶跃输入信号作用下系统时域特性及时域特性曲线。

将观测记录填写于下表中。

根轨迹起始点

根轨迹终止点

根轨迹分数

系统稳定

值范围

分离点处

值

临界稳定时

值（如果存在临界稳定点）

A11单元可调电阻值

根轨迹增益K

系统的时域特性

P.O.

Tp

Ts（δ＝5%）

仿真

实测

R=10kΩ

R=100kΩ

R=300kΩ

将根轨迹图以及时域特性曲线粘贴于下面的空白处：

2．用MATLAB绘制加入一开环极点后系统根轨迹图，观测此时系统在单位阶跃输入信号作用下系统时域特性及时域特性曲线。

3．用MATLAB绘制加入一开环零点后系统根轨迹图，观测此时系统在单位阶跃输入信号作用下系统时域特性及时域特性曲线。

1.分析原系统加入开环极点和开环零点对系统根轨迹形状和时域性能参数的变化情况，说明加入开环零点和开环极点对系统的影响。

1.参数在一定范围内取值才能使闭环系统稳定的系统称为条件稳定系统。

对于这类系统可以通过根轨迹法来确定使系统稳定的参数取值范围，也可以适当调整系统参数或增加校正网络以消除条件稳定性问题。

对于下图所示条件稳定系统：

试问能否通过增加开环零极点消除系统条件稳定性问题，即对于所有根轨迹增益，根轨迹全部位于s左半平面，闭环系统稳定。

《自动控制原理》课程实验报告（五）

频率响应和频率特性曲线的绘制

　　　　　　　　　　　　　　评阅教师签名：

1.频率响应测试实验，记录输入信号的频率，幅值和输出信号的频率、幅值以及二者之间的相位差。

序号

输入信号

输出信号

相位差

频率

幅值

0.5Hz

2

1Hz

3

5Hz

4

10Hz

5

50Hz

2.将输入信号频率为5Hz，系统频率响应的时域波形从虚拟示波器界面截图，并贴在下面空白处。

3.在测试频率特性结束后，用鼠标直接在幅频或相频特性曲线的界面上选取十点检测该点的频率特性，将该频率点的

记录到下面表格中。

f

ω

L

Im

Re

6

7

8

9

10

4．将实验过程中得到的波形截图，粘贴在如下空白处（含对数幅频曲线、对数相频曲线、幅相曲线）。

1R1=50

，C1=1

2R1=100

3R1=50

，C1=3

1．根据实验电路的具体参数，写出频率特性函数的表达式，并计算在实验频率点的幅值和相位差的理论值，与实验数据进行比较。

2．根据波德图和奈奎斯特图的关系，从测得的系统的波特图（对数幅频曲线/对数相频曲线）寻找5～10个点，手工绘制系统的奈奎斯特图形，并与实验结果比较。

1．根据一阶惯性实验电路的具体参数，确定系统传递函数，利用MATLAB进行仿真分析，当一阶惯性系统的开环增益发生（K取3个不同值）变化时，系统的频率特性曲线变化情况，将仿真结果和图形贴在下面空白处。

《自动控制原理》课程实验报告（六）

二阶系统的频率特性曲线

一、实验测试结果

1.在测试闭环系统的频率特性结束后，将系统的对数幅频曲线、对数相频曲线、幅相曲线粘贴于下面的空白处。

2.用鼠标直接在幅频或相频特性曲线的界面上点击所需增加的频率点（本实验机选取的频率值以0.1Hz为分辨率），实验机将会把鼠标点取的频率点的频率信号送入到被测对象的输入端，然后检测该频率的频率特性，将该十组频率点的

记录到表格中。

从图中读出在该组参数下，二阶闭环系统的主要性能指标：

实验值

谐振频率

谐振峰值

3.在开环系统的频率特性测试结束后，将系统的对数幅频曲线、对数相频曲线、幅相曲线粘贴于下面的空白处。

4.用鼠标直接在幅频或相频特性曲线的界面上点击所需增加的频率点（本实验机选取的频率值以0.1Hz为分辨率），实验机将会把鼠标点取的频率点的频率信号送入到被测对象的输入端，然后检测该频率的频率特性，将该十组频率点的

从图中读出在该组参数下，二阶开环系统的主要性能指标：

幅值穿越频率

相角裕度

5.改变运算模拟单元A3的开环增益，A3单元的惯性环节时间常数，A2单元的积分环节时间常数，观察系统的开环/闭环频率特性，并记录实验数据。

R

C1

C2

幅值穿越

1.根据实验电路二阶系统的传递函数和实验结果，说明该二阶系统是属于过阻尼、欠阻尼还是临界阻尼。

2.根据4组不同的实验数据，分析二阶性能参数

的变化对二阶系统的谐振频率

和谐振峰值

的影响，写出二者的公式关系。

3．根据4组不同的实验数据，分析性能参数

的变化对幅值穿越频率

，相角裕度

的影响。

四、思考题

1．根据图中系统的传递函数，利用MATLAB进行仿真分析二阶闭环系统在过阻尼、欠阻尼和是临界阻尼三种不同情况下的频率特性曲线。

《自动控制原理》课程实验报告（七）

频域法串联超前校正

1.未校正电路系统在阶跃电压信号2.5u（t）作用下，系统的时域特性参数及时域特性曲线的记录。

将所测的未校正电路系统时域特性参数记录于下表中：

上升时间Tr0

超调量P.O.0

峰值时间Tp0

调节时间Ts0（δ=5%）

将所测的未校正系统的时域特性曲线粘贴于下面的空白处：

2.未校正电路系统的开环频率特性参数及开环对数幅频、相频特性曲线（波特图）的记录。

将所测的开环频率特性参数记录于下表中：

幅穿频率ωc0

相角

pm0

将所测的未校正系统的波特图粘贴于下面的空白处：

3.串联超前校正网络设计参数的记录。

将所设计的串联超前校正网络的参数记录于下表中：

最大超前相位角

校正后系统的幅穿频率

超前校正网络的传递函数

电容C

1μF

电阻R4′10kΩ

电阻R1′

电阻R2′

电阻R3′

20kΩ

电阻αR3′

4.校正后电路系统的开环频率特性参数及开环对数幅频、相频特性曲线（波特图）的记录。

将所测的开环频率特性参数记录于下表中

幅穿频率ωc

pm

将所测的校正后系统的波特图粘贴于下面的空白处：

5.校正后电路系统在阶跃电压信号2.5u（t）作用下，系统的时域特性参数及时域特性曲线的记录。

上升时间Tr

超调量P.O.

峰值时间Tp

调节时间Ts（δ=5%）

将测得的校正后系统的时域特性曲线粘贴于下面的空白处:

１．分析校正前、后系统动态特性的变化情况，说明串联超前校正网络对系统进行超前校正时所起的作用。

1．串联超前校正网络参数变化（电阻、电容增大或减小），对系统性能有何影响？

（利用MATLAB进行仿真分析）

《自动控制原理》课程实验报告（八）

频域法串联滞后校正

1.未校正电路系统在阶跃电压信号2.5u（t）作用下，系统的时域特性参数及时域特性曲线的纪录。

将测得的未校正电路系统时域特性参数记录于下表中：

将测得的未校正系统的时域特性曲线粘贴于下面的空白处：

2.未校正电路系统的开环频率特性参数及开环对数幅频、相频曲线（波特图）的纪录。

3.串联滞后校正网络设计参数的记录。

将所设计的串联滞后校正网络的参数记录于下表中：

相位角

对数幅值

滞后校正网络的传递函数

10μF

4.校正后电路系统的开环频率特性参数及开环对数幅频、相频曲线（波特图）的纪录。

将所测的校正后电路系统的开环频率特性参数记录于下表中：

将所测的时域特性参数记录于下表中：

将所测的校正后系统的时域特性曲线粘贴于下面的空白处：

１．分析校正前、后系统性能参数的变化情况，说明串联滞后校正环节在对系统进行校正时所起的作用。

1．串联滞后校正网络参数变化（电阻、电容增大或减小）对系统性能有何影响？

《自动控制原理》课程实验报告（九）

非线性控制系统的描述函数法

1.将实验测得的由模拟电路和函数发生器产生的继电非线性环节的输出特性粘贴于下面。

模拟电路产生的图形函数发生器产生

2.运行LABACT程序，用虚拟示波器（B3）单元的观测波形，按下信号发生器（B1）阶跃信号按钮时（+5V→0阶跃），选用虚拟示波器（B3）普通示波方式观察CH1、CH2通道所输出的波形，将观测到时域响应和相轨迹截图，贴在下面空白处。

时域响应（示波方式）相轨迹（X-Y方式）

3.改变非线性单元的M值，重复实验，将实验结果和理论计算值填入下表。

M

角频率

（rad/s）

周期T（s）

振幅X（V）