完整版中考数学复习专题平行四边形动点及存在性问题文档格式.docx

完整版中考数学复习专题平行四边形动点及存在性问题文档格式.docx

《完整版中考数学复习专题平行四边形动点及存在性问题文档格式.docx》由会员分享，可在线阅读，更多相关《完整版中考数学复习专题平行四边形动点及存在性问题文档格式.docx（11页珍藏版）》请在冰豆网上搜索。

（2）当t为何值时，四边形PQCB是平行四边形？

并求出此时P、Q两点的坐标；

（3）当t为何值时，△PQC是以PQ为腰的等腰三角形？

并求出P、Q两点的坐标．

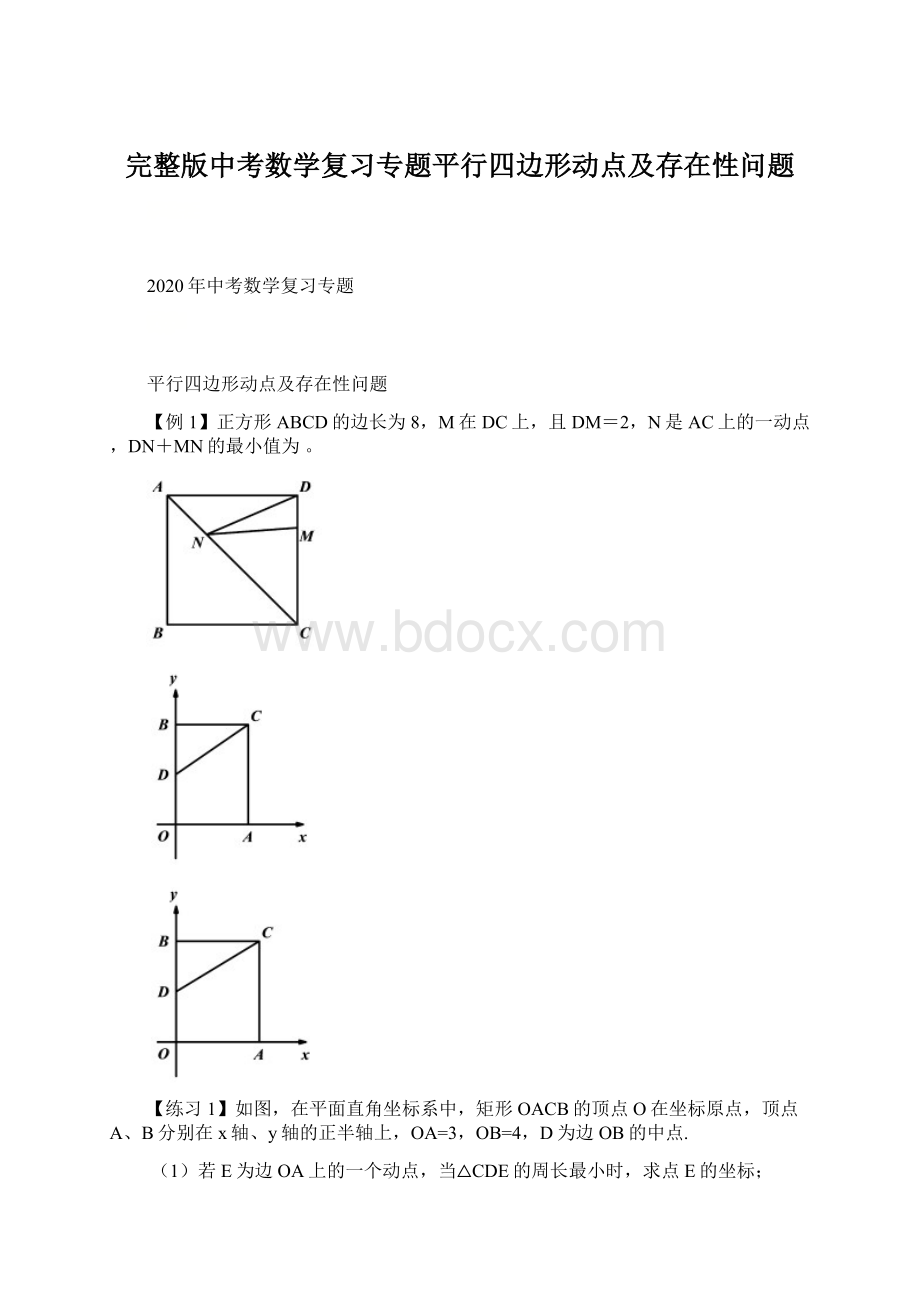
【例3】

（1）如图，矩形ONEF的对角线相交于点M，ON、OF分别在x轴和y轴上，O为坐标原点，点E的坐标为（4，3），则点M的坐标为；

（2）在直角坐标系中，有A（-1，2），B（3，1），C（1，4）三点，另有一点D与点A、B、C构成平行四边形的顶点，求点D的坐标．

【练习3】如图，四边形ABCD为矩形，C点在x轴上，A点在y轴上，D点坐标是（0，0），B点坐标是（3，4），矩形ABCD沿直线EF折叠，点A落在BC边上的G处，E、F分别在AD、AB上，且F点的坐标是（2，4）．

（1）求G点坐标；

（2）求直线EF解析式；

（3）点N在x轴上，直线EF上是否存在点M，使以M、N、F、G为顶点的四边形是平行四边形？

若存在，请直接写出M点的坐标；

若不存在，请说明理由．

【例4】在Rt△ABC中，∠B=90°

，AC=60cm，∠A=60°

，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts（0<

t

15）．过点D作DF⊥BC于点F，连接DE，EF．

（1）求证：

AE=DF；

（2）四边形AEFD能够成为菱形吗？

如果能，求出相应的t值；

如果不能，请说明理由；

（3）当t为何值时，△DEF为直角三角形？

请说明理由．

【练习4】如图，等腰三角形OAB的一边OB在x轴的正半轴上，点A的坐标为（6，8），OA=OB，动点P从原点O出发，在线段OB上以每秒2个单位的速度向点B匀速运动，动点Q从原点O出发，沿y轴的正半轴以每秒1个单位的速度向上匀速运动，过点Q作x轴的平行线分别交OA，AB于E，F，设动点P，Q同时出发，当点P到达点B时，点Q也停止运动，他们运动时间为t秒（

）

（1）点E的坐标为，F的坐标为；

（2）当t为何值时，四边形POFE是平行四边形；

（3）是否存在某一时刻，使△PEF为直角三角形？

若存在，请求出此时t的值；

【巩固练习】

1、

菱形ABCD中，AB=2，∠BAD=60°

，点E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值为。

第1题图第2题图第3题图第4题图

2、如图,在Rt△ABC中，∠ACB=90°

，∠A=30°

，AC=

，BC的中点为D,将△ABC绕点C顺时针旋转任意一个角度得到△FEC，EF的中点为G，连接DG，在旋转过程中，DG的最大值是_________；

最小值是__________．

3、已知△ABC是等腰直角三角形，∠BAC=90°

，点D是BC的中点．作正方形DEFG，连接AE，BG，若BC=DE=4，将正方形DEFG绕点D旋转，当AE取最小值时，AF=．

4、在三角形纸片ABC中，已知∠ABC=90°

，AB=6，BC=8。

过点A作直线

平行于BC，折叠三角形纸片ABC，使直角顶点B落在直线

上的T处，折痕为MN．当点T在直线

上移动时，折痕的端点M、N也随之移动．若限定端点M、N分别在AB、BC边上移动，则线段AT长度的最大值与最小值之和为____.

5、如图，在平面直角坐标系中，点A、B分别在x轴、y轴上，线段OA、OB的长（0A<

OB）

是方程组

的解，点C是直线

与直线AB的交点，点D在线段OC上，OD=

。

（1）求直线AB的解析式及点C的坐标；

（2）求直线AD的解析式；

（3）P是直线AD上的点，在平面内是否存在点Q，使以0、A、P、Q为顶点的四边形是菱形?

若存在，请直接写出点Q的坐标；

动点问题题型

图D-01

⒈如图D-01，四边形ABCD中，AD∥CB，且AD>

BD，BC=6cm，动点P、Q分别从A、C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C向B运动，几秒后四边形ABQP是平行四边形？

⒉如图D-02，在

ABC中，点O是AC边上一动点，过O作直线MN∥BC，设MN交∠ACB的平分线于E，交∠ACB的外角平分线于F，

①求证：

OE=OF

②当点O运动到何处时，四边形AECF是矩形？

证明你的结论

〖提示〗

易证∠1=∠2=∠3，得OE=OC

同理OF=OC，得证OE=OF

⒊如图D-03，矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从点A向B以2cm/s的速度移动；

点Q沿DA边从点D向A以1cm/s的速度移动；

如果P、Q同时出发，t（s）表示移动时间（0<

t<

6），那么：

1当t为何值时，

QAP为等腰直角三角形？

②求四边形QAPC的面积，并提出一个与计算结果有关的结论

图D-03

4.如图，在菱形ABCD中，AB=2，∠DAB=60°

，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．

四边形AMDN是平行四边形；

（2）填空：

①当AM的值为______时，四边形AMDN是矩形；

②当AM的值为______时，四边形AMDN是菱形．

5.如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．

（1）探究：

线段OE与OF的数量关系并加以证明；

（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？

（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？

若是，请证明，若不是，则说明理由．

6.如图，已知菱形ABCD中，∠ABC=60°

，AB=8，过线段BD上的一个动点P（不与B、D重合）分别向直线AB、AD作垂线，垂足分别为E、F．

（1）BD的长是______；

（2）连接PC，当PE+PF+PC取得最小值时，此时PB的长是______．

7.如图，矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q。

OP=OQ；

（2）若AD=8厘米，AB=6厘米，P从点A出发，以1厘米/秒的速度向D运动（不与D重合）。

设点P运动时间为t秒，请用t表示PD的长；

并求t为何值时，四边形PBQD是菱形。

8.如图，已知矩形ABCD，AD=4，CD=10，P是AB上一动点，M、N、E分别是PD、PC、CD的中点．

四边形PMEN是平行四边形；

（2）请直接写出当AP为何值时，四边形PMEN是菱形；

（3）四边形PMEN有可能是矩形吗？

若有可能，求出AP的长；

若不可能，请说明理由．

9.已知：

如图，在□ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G。

△ADE≌△CBF；

（2）若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？

并证明你的结论。

10.如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F是AC上两动点，分别从A，C两点以相同的速度向C、A运动，其速度为0.5cm／s。

（1）当E与F不重合时，四边形DEBF是平行四边形吗？

说明理由；

（2）点E，F在AC上运动过程中，以D、E、B、F为顶点的四边形是否可能为矩形？

如能，求出此时的运动时间t的值，如不能，请说明理由。

11.

如图，平行四边形ABCD中，AB⊥AC，AB=1，BC=

，对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．

（1）证明：

当旋转角为90°

时，四边形ABEF是平行四边形；

（2）试说明在旋转过程中，线段AF与EC总保持相等；

（3）在旋转过程中，四边形BEDF可能是菱形吗？

如果能，说明理由并求出此时AC绕点O顺时针旋转的度数．

12.如图，在△ABC中，∠ACB=90°

，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF=CE=AE．

（1）说明四边形ACEF是平行四边形；

（2）当∠B满足什么条件时，四边形ACEF是菱形，并说明理由

13.如图，在菱形ABCD中，P是AB上的一个动点（不与A、B重合），连接DP交对角线AC于E连接BE．

∠APD=∠CBE；

（2）若∠DAB=60°

，试问P点运动到什么位置时，△ADP的面积等于菱形ABCD面积的

为什么？

14.在边长为6的菱形ABCD中，动点M从点A出发，沿A⇒B⇒C向终点C运动，连接DM交AC于点N．

（1）如图1，当点M在AB边上时，连接BN：

①求证：

△ABN≌△ADN；

②若∠ABC=60°

，AM=4，∠ABN=α，求点M到AD的距离

（2）如图2，若∠ABC=90°

，记点M运动所经过的路程为x（6≤x≤12）．试问：

x为何值时，△ADN为等腰三角形．