推理方法综述Word下载.docx

推理方法综述Word下载.docx

《推理方法综述Word下载.docx》由会员分享，可在线阅读，更多相关《推理方法综述Word下载.docx（9页珍藏版）》请在冰豆网上搜索。

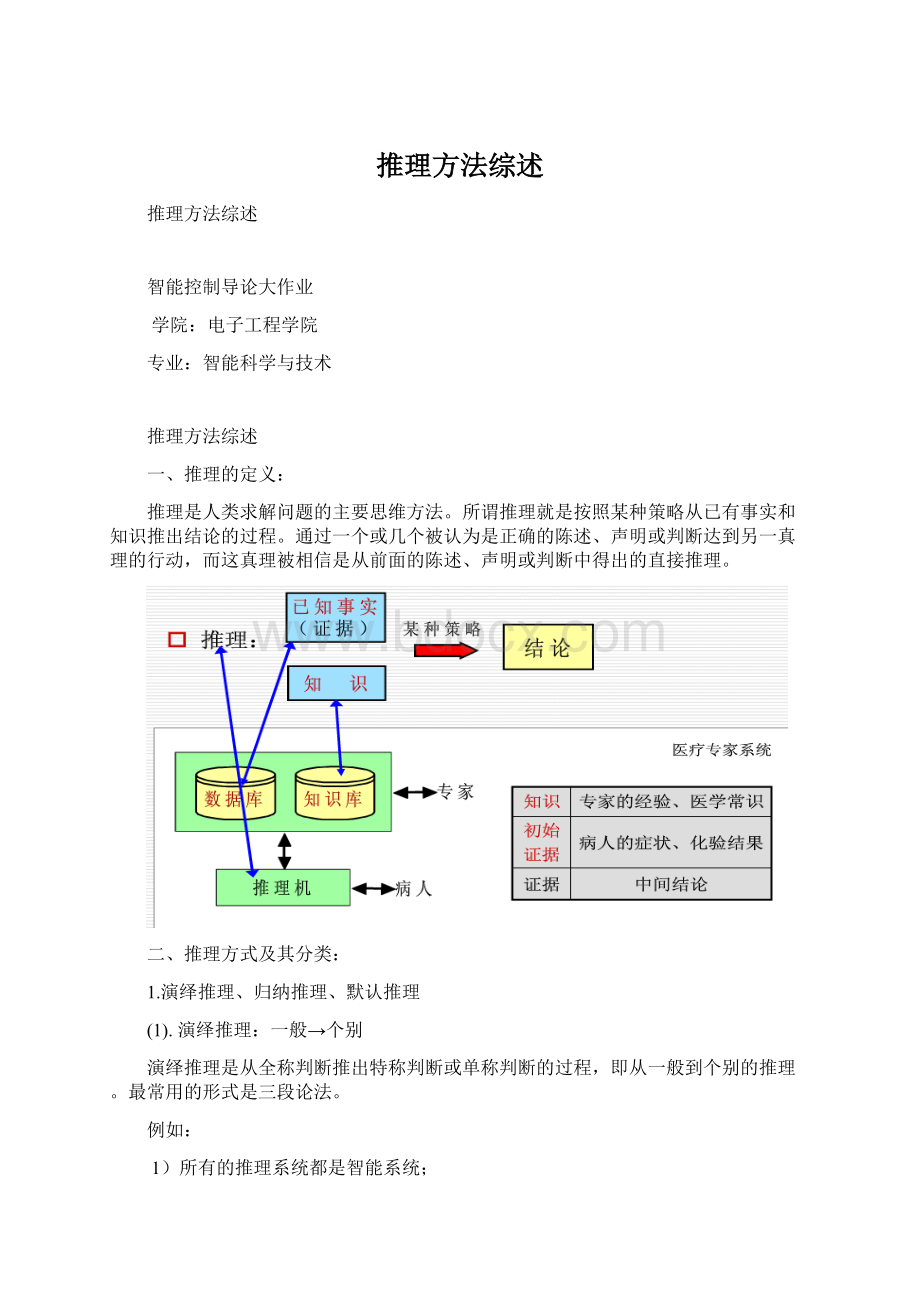
二、推理方式及其分类：

1.演绎推理、归纳推理、默认推理

（1）.演绎推理：

一般→个别

演绎推理是从全称判断推出特称判断或单称判断的过程，即从一般到个别的推理。

最常用的形式是三段论法。

例如：

1）所有的推理系统都是智能系统；

2）专家系统是推理系统；

3）所以，专家系统是智能系统。

（2）.归纳推理:

个别→一般

是从足够多的事例中归纳出一般性结论的推理过程，是一种从个别到一般的推理过程，分为完全归纳推理，又称为必然性推理，不完全归纳推理，又称为非

如果按推理中是否运用与问题有关的启发性知识，推理可分为启发式推理和非启发式推理。

（1）启发式推理。

如果在推理过程中，运用与问题有关的启发性知识，如解决问题的策略、技巧及经验等，以加快推理过程，提高搜索效率，这种推理过程称为启发式推理。

如A、A*等算法。

（2）非启发式推理。

如果在推理过程中，不运用启发性知识，只按照一般的控制逻辑进行推理，这种推理过程称为非启发式推理。

（推理效率较低，容易出现“组合爆炸”问题。

）

三、推理的控制策略：

主要是指推理方向的选择、推理时所用的搜索策略及冲突解决策略等。

一般推理的控制策略与知识表达方法有关（产生式系统）。

基于规则的演绎推理

1、推理方向：

用于确定推理的驱动方式。

分为正向推理（由已知事实出发）、反向推理（以某个假设目标作为出发点）和正反向混合推理（正向推理和反向推理相结合）.系统组成:

知识库（KB）+初始事实和中间结果的数据库（DB）+推理机

（1）.正向推理（事实驱动推理）:

已知事实→结论

基本思想：

正向推理又称数据驱动推理，是按照由条件推出结论的方向进行的推理方式，它从一组事实出发，使用一定的推理规则，来证明目标事实或命题的成立。

一般的推理过程是先向综合数据库提供一些初始已知事实，控制系统利用这些数据与知识库中的知识进行匹配，被触发的知识，将其结论作为新的事实添加到综合数据库中。

重复上述过程，用更新过的综合数据库中的事实再与知识库中另一条知识匹配，将其结论更新至综合数据库中，直到没有可匹配的新知识和不再有新的事实加入到综合数据库中为止。

然后测试是否得到解，有解则返回解，无解则提示运行失败。

实现正向推理需要解决的问题：

①确定匹配（知识与已知事实）的方法。

②按什么策略搜索知识库。

③冲突消解策略。

特点：

正向推理简单，易实现，但目的性不强，效率低。

（2）.逆向推理（目标驱动推理）：

以某个假设目标作为出发点。

①选定一个假设目标。

②寻找支持该假设的证据，若所需的证据都能找到，则原假设成立；

若无论如何都找不到所需要的证据，说明原假设不成立的；

为此需要另作新的假设。

主要优点：

不必使用与目标无关的知识，目的性强，同时它还有利于向用户提供解释。

主要缺点：

起始目标的选择有盲目性。

实现逆向推理需要解决的问题：

①如何判断一个假设是否是证据？

②当导出假设的知识有多条时，如何确定先选哪一条？

③一条知识的运用条件一般都有多个，当其中的一个经验证成立后，如何自动地换为对另一个的验证？

目的性强，利于向用户提供解释，但选择初始目标时具有盲目性，比正向推理复杂。

（3）.混合推理

正反向混合推理：

（1）先正向后逆向：

先进行正向推理，帮助选择某个目标，即从已知事实演绎出部分结果，然后再用逆向推理证实该目标或提高其可信度；

（2）先逆向后正向：

先假设一个目标进行逆向推理，然后再利用逆向推理中得到的信息进行正向推理，以推出更多的结论。

（4）.双向推理

双向推理：

正向推理与逆向推理同时进行，且在推理过程中的某一步骤上“碰头”的一种推理。

2、搜索策略:

推理时要反复用到知识库中的规则，而知识库中的规则又很多，这样就存在着如何在知识库中寻找可用规则的问题（代价小,解好）.可以采用各种搜索策略有效地控制规则的选取.

3、冲突解决策略：

在推理过程中，系统要不断地用数据库中的事实与知识库中的规则进行匹配，当有一个以上规则的条件部分和当前数据库相匹配时，就需要有一种策略来决定首先使用哪一条规则，这就是冲突解决策略。

冲突解决策略实际上就是确定规则的启用顺序。

（1）专一性排序（条件部分更具体的规则）

（2）规则排序（规则编排顺序）

（3）数据排序（所有条件按优先级次序编排起来）

（4）就近排序（最近使用的规则优先）

（5）上下文限制（在某种上下文条件下）

（6）按匹配度排序（计算这两个模式的相似程度）

（7）按条件个数排序（条件少的优先）

不确定性推理：

1、概率方法

概率推理就是由给定的变量信息来计算其它变量的概率信息的过程。

假设给定证据集合E为变量集合Y的子集，其中变量取值用e表示，即E=e，此时若希望计算条件概率

的值，即在给定证据变量取值后求变量

的概率，这个过程被称为概率推理。

在基于概率的不确定推理中，概率一般解释为专家对证据和规则的主观信任度。

对概率推理起着支撑作用的是Bayes公式。

Bayes公式用于不确定推理的一个原始条件是：

已知前提E的概率P（E）和H的先验概率P（H），并已知H成立时E出现的条件概率P（E|H）。

推理的目的是推出H的后验概率P（H|E）。

如果有多个证据E1，E2，...，Em和多个结论H1，H2，....，Hn，并且每个证据都以一定程度支持结论，则

此时，只要已知Hj的先验概率P（Hj）及Hi成立时证据E1，E2，...，Em出现的条件概率P（E1|Hj），P（E2|Hj），...，P（Em|Hj），就可利用上述计算出在E1，E2，...，Em出现的情况下的条件概率P（Hi|E1，E2，...，Em）。

2、模糊推理方法

从不精确的前提集合中得出可能的不精确结论的推理过程，又称近似推理。

在人的思维中，推理过程常常是近似的。

例如，人们根据条件语句（假言）“若西红柿是红的”，则西红柿是熟的”和前提（直言）“西红柿非常红”，立即可得出结论“西红柿非常熟”。

这种不精确的推理不可能用经典的二值逻辑或多值逻辑来完成。

人类思维判断的基本形式：

如果（条件）→则（结论）

“如果炉温低则应施加高电压”

设x：

“炉温”，A：

“低炉温”，y：

“电压”，B：

“高电压”，则上述规则可表示为

“如果x是A，则y是B”，记为A→B

最常用的模糊蕴含运算：

模糊蕴含最小运算

广义的肯定式推理方式：

前提1：

x是A’

前提2：

如果x是A，则y是B

结论：

y是B

模糊推理公式：

B’=A’。

（A→B）=A’。

R