3高中数学三角函数知识点总结Word文件下载.docx

3高中数学三角函数知识点总结Word文件下载.docx

《3高中数学三角函数知识点总结Word文件下载.docx》由会员分享，可在线阅读，更多相关《3高中数学三角函数知识点总结Word文件下载.docx（25页珍藏版）》请在冰豆网上搜索。

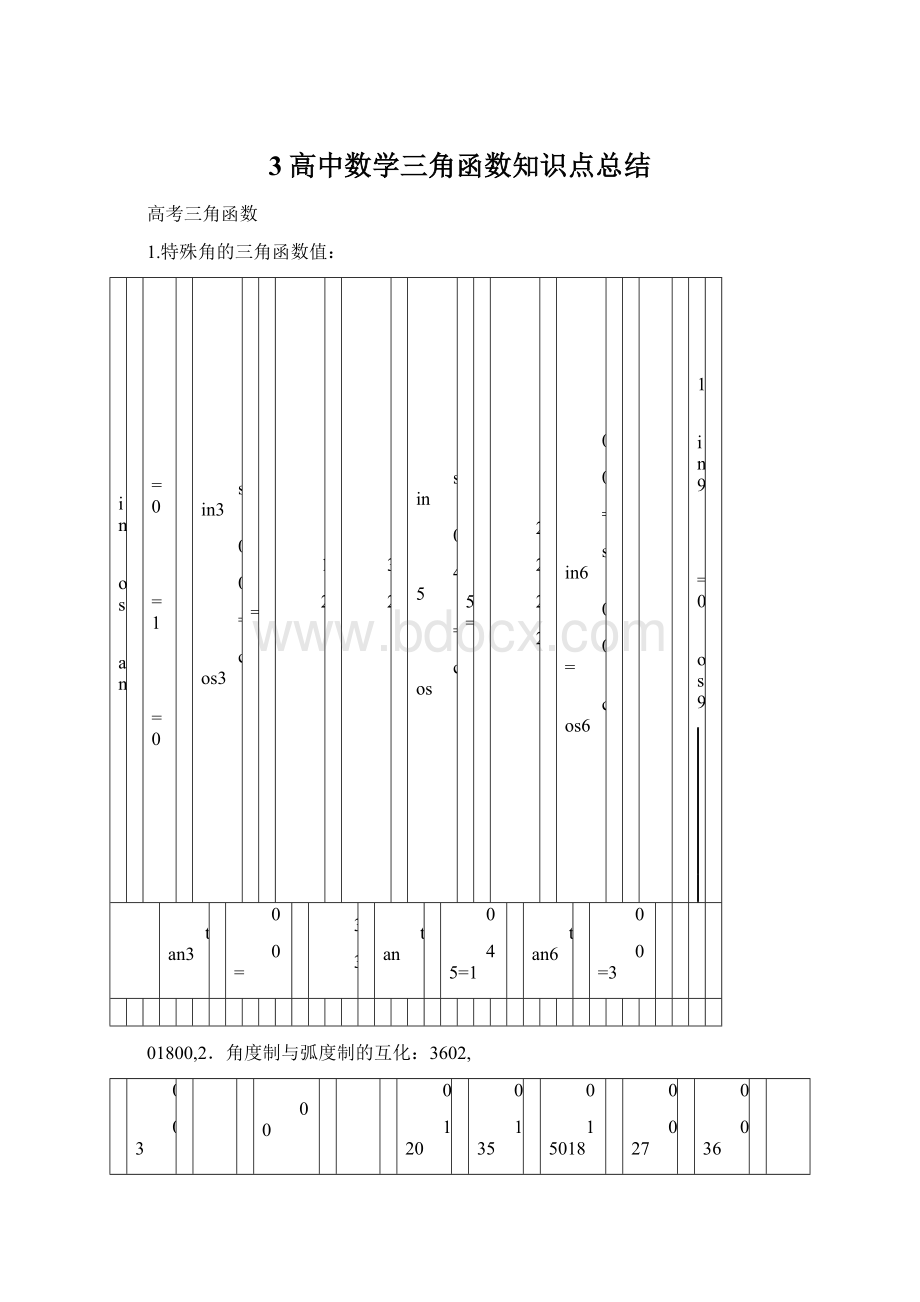
03

00

45609

120

135

15018

027

036

235320

64323462

3.弧长及扇形面积公式

弧长公式：

l.r扇形面积公式:

S=l.r

----是圆心角且为弧度制。

r-----是扇形半径

4.任意角的三角函数

设是一个任意角，它的终边上一点p（x,y）,r=

x

2y

（1）正弦sin=

y

r

余弦cos=

正切tan=

（2）各象限的符号：

yy

+

—+

2O

cossin

——

O

+—

sincostan

2.同角三角函数的基本关系：

（1）平方关系：

sin2+cos2=1。

（2）商数关系：

=tan

（k,kz

）

3.诱导公式：

1sin2ksin，cos2kcos，tan2ktank．

2sinsin，coscos，tantan．

3sinsin，coscos，tantan．

4sinsin，coscos，tantan．

口诀：

函数名称不变，符号看象限．

5sincos

，cossin

．

6sincos

正弦与余弦互换，符号看象限．

7正弦函数、余弦函数和正切函数的图象与性质

8、三角函数公式：

倍角公式

两角和与差的三角函数关系

sin2=2sin·

sin（）=sin·

coscos·

2-sin2

cos2=cos

降幂公式：

升幂公式：

cos（）=cos·

cossin·

1cos

1+cos=cos

2cos

22

tantan

tan（）

21tantan

2sin

1-cos=sin

正弦定理：

9．

abc

2R

.

sinAsinBsinC

余弦定理：

222

abcbcA

;

bcacaB

cababC

cos2

2-1

=2cos

=1-2sin

2tan

1tan

三角形面积定理.

111

SabsinCbcsinAcasinB.

1．直角三角形中各元素间的关系：

如图，在△ABC中，C＝90°

，AB＝c，AC＝b，BC＝a。

（1）三边之间的关系：

a2＋b2＝c2。

（勾股定理）

（2）锐角之间的关系：

A＋B＝90°

；

（3）边角之间的关系：

（锐角三角函数定义）

sinA＝cosB＝

a

c

，cosA＝sinB＝

b

，tanA＝

。

2．斜三角形中各元素间的关系：

在△ABC中，A、B、C为其内角，a、b、c分别表示A、B、C的对边。

（1）三角形内角和：

A＋B＋C＝π。

（2）正弦定理：

在一个三角形中，各边和它所对角的正弦的比相等

ab

sinAsinB

（R为外接圆半径）

C

（3）余弦定理：

三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两

倍

2＝b2＋c2－2bccosA；

b2＝c2＋a2－2cacosB；

c2＝a2＋b2－2abcosC。

3．三角形的面积公式：

（1）△＝

aha＝

bhb＝

chc（ha、hb、hc分别表示a、b、c上的高）；

（2）△＝

absinC＝

bcsinA＝

acsinB；

4．解三角形：

由三角形的六个元素（即三条边和三个内角）中的三个元素（其中至少有一个是边）

求其他未知元素的问题叫做解三角形．广义地，这里所说的元素还可以包括三角形的高、中线、角平分

线以及内切圆半径、外接圆半径、面积等等．解三角形的问题一般可分为下面两种情形：

若给出的三角

形是直角三角形，则称为解直角三角形；

若给出的三角形是斜三角形，则称为解斜三角形

解斜三角形的主要依据是：

设△ABC的三边为a、b、c，对应的三个角为A、B、C。

（1）角与角关系：

A+B+C=π；

（2）边与边关系：

a+b>

c，b+c>

a，c+a>

b，a－b<

c，b－c<

a，c－a>

b；

（3）边与角关系：

正弦定理2R

（R为外接圆半径）；

余弦定理c2=a2+b2－2bccosC，b2=a2+c2－2accosB，a2=b2+c2－2bccosA；

它们的变形形式有：

a=2RsinA，

A

B

，

2bc

5．三角形中的三角变换

三角形中的三角变换，除了应用上述公式和上述变换方法外，还要注意三角形自身的特点。

（1）角的变换

因为在△ABC中，A+B+C=π，所以sin（A+B）=sinC；

cos（A+B）=－cosC；

tan（A+B）=－tanC。

AB

CA

四．【典例解析】

题型1：

正、余弦定理

（2009岳阳一中第四次月考）.已知△ABC中，ABa，ACb，ab0，

15

S，

ABC

4

a3,b5，则BAC（）

A.．30B．150C．

150D．30或

150

答案C

例1．

（1）在ABC中，已知

A32.0，

B81.8，a42.9cm，解三角形；

（2）在ABC中，已知a20cm，b28cm，

A40，解三角形（角度精确到

1，边长精确到

1cm）。

解析：

（1）根据三角形内角和定理，

C180（AB）

000

180（32.081.8）

4.；

根据正弦定理，

asinB42.9sin81.8

b80.1（cm）

sinAsin32.0

0asinC42.9sin66.2

c74.1（cm）.

（2）根据正弦定理，

bsinA28sin40

sinB0.8999.

a20

因为

0＜B＜180，所以

B64，或

116.

①当

B64时，

00000

C180（AB）180（4064）76，

0asinC20sin76

c30（cm）.

sinAsin40

②当

B116时，

C180（AB）180（40116）24，

asinC20sin24

c13（cm）.

点评：

应用正弦定理时

（1）应注意已知两边和其中一边的对角解三角形时，可能有两解的情形；

（2）

对于解三角形中的复杂运算可使用计算器

例2．

（1）在ABC中，已知a23，c62，

B60，求b及A；

（2）在ABC中，已知a134.6cm，b87.8cm，c161.7cm，解三角形

（1）∵

2222cos

bacacB

（23）（62）223（62）cos

12（62）43（31）=

=8

∴b22.

求A可以利用余弦定理，也可以利用正弦定理：

解法一：

∵cos

222（22）2（62）2（23）21

bca

2222（62）2

bc

∴

60.

解法二：

∵sin

a23

AsinBsin45,

又∵62＞2.41.43.8,23＜21.83.6,∴a＜c，即

0＜A＜

90,

（2）由余弦定理的推论得：

5.161.7134.6

287.8161.7

5.,

A5620；

cab

2ca

134.6161.787.8

2134.6161.7

0.8398,

B3253；

0000

C180（AB）180（56203253）

9047.

应用余弦定理时解法二应注意确定A的取值范围。

题型2：

三角形面