数学建模猎狗追兔子问题Word格式.docx

数学建模猎狗追兔子问题Word格式.docx

《数学建模猎狗追兔子问题Word格式.docx》由会员分享，可在线阅读，更多相关《数学建模猎狗追兔子问题Word格式.docx（12页珍藏版）》请在冰豆网上搜索。

关键词

微分方程导数的几何意义猎狗追兔子数学建模数学软件

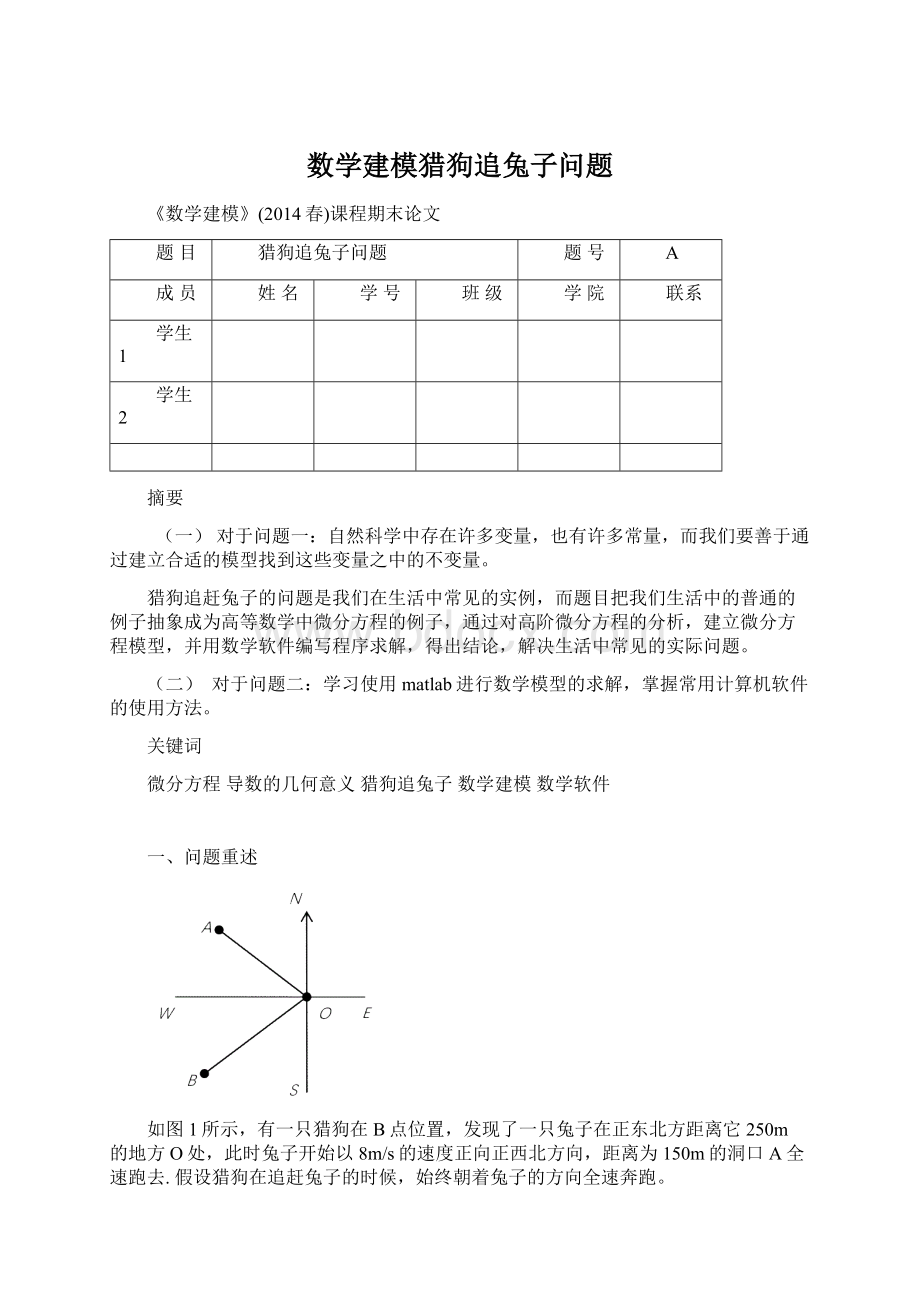
一、问题重述

如图1所示，有一只猎狗在B点位置，发现了一只兔子在正东北方距离它250m的地方O处，此时兔子开始以8m/s的速度正向正西北方向，距离为150m的洞口A全速跑去.假设猎狗在追赶兔子的时候，始终朝着兔子的方向全速奔跑。

请回答下面的问题：

⑴猎狗能追上兔子的最小速度是多少？

⑵在猎狗能追上兔子的情况下，猎狗跑过的路程

是少？

⑶假设猎狗在追赶过程中，当猎狗与兔子之间的

距离为30m时，兔子由于害怕导致奔跑速度每秒减半，

而狗却由于兴奋奔跑速度每秒增加0.1倍，在这种情

况下回答前面两个问题。

二、问题分析与假设

在猎狗追赶兔子的时候猎狗一直朝着兔子的方向追赶，所以可以建立平面直角坐标系，通过导数联立起猎狗运动位移，速度和兔子的运动状态。

1.假设兔子的运动是匀速的。

2.假设猎狗的运动轨迹是一条光滑并且一阶导数存在的曲线。

3.猎狗的运动时匀速或者匀变速的。

4.猎狗运动时总是朝向兔子。

三、模型的建立及求解

3.1符号规定

1.（x，y）：

猎狗或者兔子所在位置的坐标。

2.t：

从开始到问题结束经过的时间。

3.a:

猎狗奔跑的路程。

4.

v:

猎狗的奔跑速度。

3.2模型一的建立与求解

猎狗能够抓到兔子的必要条件：

猎狗的运动轨迹在OA要有交点

以OA为y轴，以OB为x轴建立坐标系，则由图有O（0，0），A（0,150）,B（250，0），兔子的初始位置0点,而猎狗初始位置是B点，t（s）后猎狗到达了C（x，y），而兔子到达了D（0，8t），则有CD的连线是猎狗运动轨迹的一条切线，由导数的几何意义有：

三式联立消去t，得到;

设：

若猎狗可以追上兔子则有当兔子在OA,猎狗在OB之间运动时此方程有解，设：

得到：

两式联立相加得到：

1.如果q=1即v=8m/s得到

所以此情况无交点，所以v=8m/s猎狗无法追上兔子；

2.如果q<

1即v>

8m/s得到

此情况有交点，所以有可能能够追上兔子，如果要追上兔子需要y<

=150;

解得到：

即

所以这种情况下能够追上的最小速度是

.

3.如果q>

1利用上式得到

，所以这种情况不能追上兔子。

综上讨论，猎狗可以追上兔子的最小速度为

。

3.3模型二的建立与求解

如果猎狗可以追上兔子那么猎狗的轨迹和兔子的轨迹必相交与一点，此时兔子的路程

，所用放的时间

，那么猎狗的的路程a=tv;

带入数值解得a=

3.4模型三的建立与求解

模型三利用matlab试验，得到代码如下：

a=8;

dogxa=[];

dogya=[];

rabbitxa=[];

rabbitya=[];

d=1;

dogx=250;

dogy=0;

rabbitx=0;

rabbity=0;

t=0;

dt=0.001;

forb=0:

100

dogx=250;

dogy=0;

rabbitx=0;

rabbity=0;

t=0;

c=b;

a=8;

while（sqrt（（dogx-rabbitx）^2+（dogy-rabbity）^2）>

d&

rabbity<

150）

if（sqrt（（dogx-rabbitx）^2+（dogy-rabbity）^2）<

=30）

b=b*1.1^dt;

a=a*0.5^dt;

end

t=t+dt;

dogx=dogx+b*dt*（rabbitx-dogx）/sqrt（（dogx-rabbitx）^2+（dogy-rabbity）^2）;

dogy=dogy+b*dt*（rabbity-dogy）/sqrt（（dogx-rabbitx）^2+（dogy-rabbity）^2）;

rabbitx=rabbitx+0;

rabbity=rabbity+a*dt;

if（rabbity<

=150）

b=c;

break;

end

fprintf（'

猎狗的最小速度是：

:

%2f'

b）;

b=16;

dogxb=[];

dogyb=[];

rabbitxb=[];

rabbityb=[];

s=0;

while（sqrt（（dogx-rabbitx）^2+（dogy-rabbity）^2）>

d）

dogx0=dogx;

dogy0=dogy;

dogx=dogx+b*dt*（rabbitx-dogx）/sqrt（（dogx-rabbitx）^2+（dogy-rabbity）^2）

dogy=dogy+b*dt*（rabbity-dogy）/sqrt（（dogx-rabbitx）^2+（dogy-rabbity）^2）

dogxb=[dogxb,dogx];

dogyb=[dogyb,dogy];

rabbitxb=[rabbitxb,rabbitx];

rabbityb=[rabbityb,rabbity];

s=s+sqrt（（dogx0-dogx）^2+（dogy0-dogy）^2）;

最短路程是：

%1f'

s）;

得到猎狗的最小速度是：

16m/s

猎狗此时的路程是：

312.5m

四、模型的检验

使用matlab进行计算机模拟实验检验模型的可行性：

问题一的检验：

h=250;

v=16;

d=0.01;

dt=0.1;

dogx=h;

while（（sqrt（dogx-rabbitx）^2+（dogy-rabbity）^2）>

&

t<

=19.3）

t=dt+t;

dogx=dogx-v*dt*dogx/sqrt（dogx^2+（a*t-dogy）^2）;

dogy=dogy+v*dt*（a*t-dogy）/sqrt（dogx^2+（a*t-dogy）^2）;

rabbity=a*t;

rabbitxb=zeros（length（rabbityb））;

plot（dogxb,dogyb,rabbitxb,rabbityb,'

*'

）

问题二的模拟：

n=250;

d=0.1;

dx=n;

dy=0;

rx=0;

ry=0;

while（sqrt（（dx-rx）^2+（dy-ry）^2）>

19.3）

plot（dx,dy,rx,ry,'

y*'

pause（0.00001）

holdon

t=dt+t;

dx=dx-v*dt*dx/sqrt（dx^2+（a*t-dy）^2）;

dy=dy+v*dt*（a*t-dy）/sqrt（dx^2+（a*t-dy）^2）;

ry=a*t;

plot（dx,dy,rx,ry,'

五、模型的评价

5.1模型的优缺点

模型的优点。

（1）模型的使用围比较广泛，可以类推到其他许多模型中。

（2）模型具有很高的使用价值。

（3）模型对题目中的问题解决合适，模型使用得当。

这里写模型的缺点。

（4）题目中增加了一些理想化的假设，致使模型的波动比较大。

（5）不同兔子和猎狗的情况会有差异。

5.2模型的改进

可使用仿生学原理，建立我们更加准确的模型。

六、参考文献

[1]书来，MATLAB编程与最优化问题，：

电子工业，2013。

[2]邬学军，周凯，宋军全，数学建模竞赛辅导教程，，大学，2009。

[3]志林，欧宜贵，数学建模及其典型案例分析，，化学工业，2006.

[4]Matlab入门教程,wenku.baidu./view/daf8592fff00bed5b9f31d5d.htl

2014.06

附录1：

Matlab的截图