第五届日本算术奥林匹克竞赛预赛试题Word版含答案Word下载.docx

第五届日本算术奥林匹克竞赛预赛试题Word版含答案Word下载.docx

《第五届日本算术奥林匹克竞赛预赛试题Word版含答案Word下载.docx》由会员分享，可在线阅读，更多相关《第五届日本算术奥林匹克竞赛预赛试题Word版含答案Word下载.docx（8页珍藏版）》请在冰豆网上搜索。

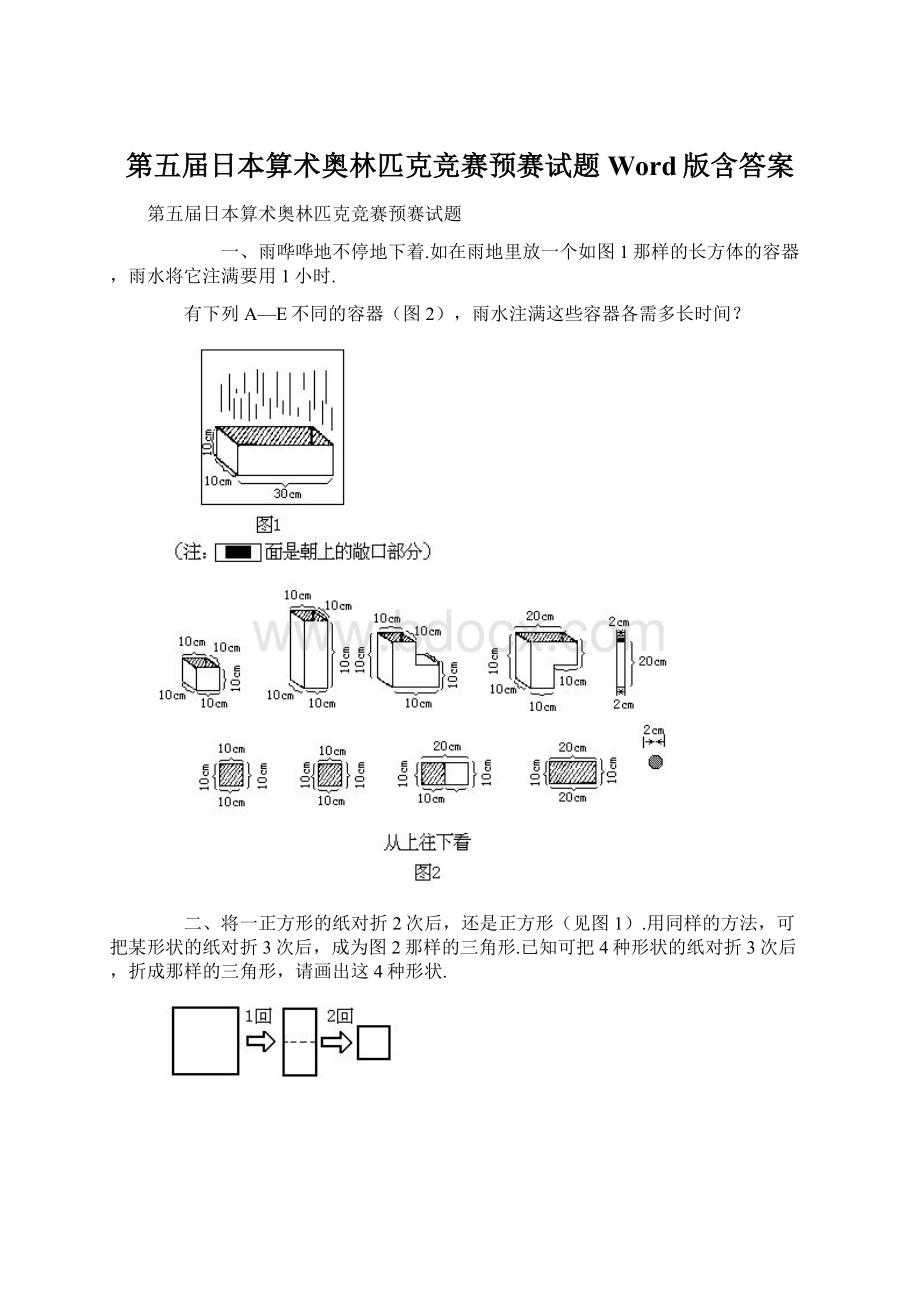
　　四、有193个人坐成一横排.

　　首先，正中间的一个人站起来，然后，按下述方法大家都或坐或站.

　　①邻座的人站起来，1秒钟后，自己也站起来.

　　②站起1秒钟后坐下.

　　③如果左右邻座的人同时是站着的话，即使过了1秒钟，自己仍然坐着.

（1）最初的那个人站起8秒钟后，有几个人站着？

（2）96秒钟后，有几个人站着？

　　五、有一个如图那样的方块网格，每1个小方块里有1个人，在这些人中间，有人戴着帽子，有人没戴.每一个人都只能看见自己前方，后方和斜方的人的头，如图1所示，A方块里的人能看见8个人的头，B方块里的人能看见5个人的头，C方块里的人能看见3个人的头，自己看不见自己的头.在图2的方格中，写着不同方块里的人能看见的帽子的数量，那么，请在图2中找出有戴帽子的人的方块，并把它涂成黑色.

　　六、某俱乐部有11个成员，他们的名字分别是A～K.这些人分为两派，一派人总说实话，另一派人总说谎话.某日，老师问：

“11个人里面，总说谎话的有几个人？

”那天，J和K休息，余下的9个人这样回答：

　　A说：

“有10个人.”

　　B说：

“有7个人.”

　　C说：

“有11个人.”

　　D说：

“有3个人.”

　　E说：

“有6个人.”

　　F说：

　　G说：

“有5个人.”

　　H说：

　　I说：

“有4个人.”

　　那么，这个俱乐部的11个成员中，总说谎话的有几个人？

　　七、有50张卡片，每一张都分别写着从1到50的数字（见图）.卡片的两面一面是红色，一面是蓝色，两面都写着相同的数字.有一个班正好有50名学生，老师把这50张卡片都将蓝色朝上地摆在桌上，对同学们说：

“请你们按学号的顺序逐个到前面来翻卡片，规则是：

只要卡片上的数字是你自己学号的倍数，你就把它们都翻过来，蓝的就翻成红的，红的就翻成蓝的.”

　　那么，到最后，学号是50的学生按老师的要求翻完以后，红色朝上的卡片有多少张？

　　八、如图所示，把边长为6cm的等边三角形剪成4部分，从三角形顶点往下1cm处，呈30°

角下剪刀，使中间部分形成一个小的等边三角形.

所有斜线部分的面积是中间小等边三角形的面积的几倍？

　　九、有同样大小的立方体27个，把它们竖3个，横3个，高3个，紧密地没有缝隙地搭成一个大的立方体（见九题图）.

　　如果用1根很直的细铁丝扎进这个大立方体，最多可以穿透几个小立方体？

附：

第五届日本算术奥林匹克竞赛预赛试题解析

　　一、解题中“雨哗哗地不停地下着”这一条件，也可以理解为雨均匀地下.（这与日常生活中的降雨略有不同，生活中降雨可能会时大时小，并不均匀.）雨水从敞口部分垂直落入到容器内，我们就可以把“敞开面”（即图中所示的阴影面）叫做“接雨面”.图中所示的长方体容器，“接雨面”与底面大小相同，雨水将它下满需要1小时，也就是说1小时后该容器内雨水的深度是10cm.如果容器的高度不止10cm，而是无限的，那么2小时后容器内雨水的深度将会是2cm，以后每过1小时雨水的深度就会增加10cm；

如果在长方体容器中垂直放入一个很薄的挡板（其厚度忽略不计），将大容器分成两个小容器（如图所示）.小容器的“接雨面”变小了，但每个小容器的“接雨面”与底面大小仍然相同.那么1小时后，每个小容器内雨水的深度还是10cm.（因为忽略了挡板的厚度，它不占原来长方体容器的容积.）通过上述分析与假设，我们可得出如下结论：

只要容器的“接雨面”与底面大小相同，1小时后容器内雨水的深度就是10cm.

　　根据结论，观察图2所示的五种容器.其中A、B、E三种容器的“接雨面”与底面大小相同.

　　A容器高10cm，雨水下满该容器需要1小时；

　　B容器高30cm，雨水下满该容器需要3小时；

E容器高20cm，雨水下满该容器需要2小时.

　　剩下C、D两种容器，它们的“接雨面”与底面大小不同，可先将其转化为“接雨面”与底面大小相同的容器（如图所示）.此时，C容器的高变为30cm，雨水下满需3小时；

D容器的高变为15cm，雨水下满需1.5小时.

二、解（见下图）

三、解由图1可知：

　　①＋②＋③＜④＋⑤＋⑥＋⑦（一式）

　　由图2可知：

　　②＋⑥＋⑧＞①＋③＋④＋⑤（二式）

　　由图3可知：

　　①＋③＋⑧＜②＋④＋⑤（三式）

　　观察三式可得出如下结论：

①、③、⑧中不可能有克重的球，②、④、⑤中必有重量超过1克的球.

　　观察二式可得结论：

④、⑤两球重量均为1克，（因为如果其中有重2克的，则②、⑥、⑧重量之和最多与①、③、④、⑤重量之和相等，图2将不成立，与已知矛盾.）

　　观察一式可得结论：

①、②、③中没有重3克的球.（否则图1所示状态将不成立）

　　综合上述3条结论可知：

②号球重2克，①、③、⑧、④、⑤的重量均为1克.

　　再次观察二式可知：

⑥号球重3克.

四、解（找规律）（用△表示站，○表示坐）

　　上表第1个方框内的2表示第1秒后有2人站着；

第2个方框内有两个数，上面2表示第2秒后有2人站着，下面的4表示第3秒后有4人站着.三角内的两个数为所求，即：

第8秒后有2人站着，第96秒后有4人站着.

五、解答案如下图所示.

分析①站在第一行第五列的人能看见1顶帽子，说明他周围的3人有2人没戴帽子.

　　②站在第二行第四列的人能看见7顶帽子，说明他周围的8人中只有1人没戴帽子，综合结论①可知他本人没有戴帽子.

　　③站在第二行第五列的人能看到4顶帽子，且他周围的5人中已有1人没戴帽子，说明其余4人均戴帽子，根据结论①可知他本人没戴帽子.

　　④利用上下对称原理可以分析出：

站在第四行、第五行后三列的6个人中，只有第四行第四列、第五列两人没戴帽子，其他人均戴帽子.

　　⑤站在第四行第二列的人能看到7顶帽子，说明他周围的8人中只有1人没戴帽子.

　　⑥站在第三行第1列的人能看见1顶帽子，说明他周围的5人中只有1人戴帽子.综合结论⑤可知：

这1人不可能是第二行第一二列的人，也不可能是第四行第二列的人.所以只能是站在第三行第二列的人或第四行第一列的人.

　　⑦站在第五行第一列的人能看到2顶帽子，说明结论⑥所说戴帽子的人站在第四行第一列.

　　⑧站在第二行第二列的人能看到6顶帽子，说明站在第一行第一、二列的2人都戴帽子.

　　综合上述分析，可以看到“思考的顺序”是解答本题的关键.

六、解因为9个人回答出了7种不同的人数，而且回答相同的最多是两个人.所以说谎话的不少于7人.若说谎话的有7人，则除B外，其它回答问题的8人均说了谎话，与假设出现矛盾；

若说谎话的有8人，则回答问题的9人均说了谎话，出现矛盾；

若说谎话的有10人，则只能1人说实话，而A和F都说了实话，出现了矛盾；

若说谎话的有11人，则没有说实话的，而C说了实话，出现矛盾；

显然说谎话的有9人，回答问题的9人均说谎话，休息的两人说实话.

七、解每张卡片，所写数字有几个约数就被翻过几次.被翻了奇数次的卡片红色面朝上，而只有完全平方数才能有奇数个约数，所以本题也就是求写有完全平方数的卡片有几张，所以红色朝上的卡片共有7张.

八、解将大三角形分成边长1cm的小等边三角形即可求解.大三角形中包含36个小等边三角形，空白三角形包含3个小等边三角形.所以

九、解首先从简单的想起，研究铁丝穿透1个小立方体时，应从哪面穿入，哪面穿出.然后考虑铁丝扎进8个小立方体搭成的较大立方体，最多可以穿透几个小立方体.最后再考虑扎进27个小立方体搭成的大立方体时，最多可以穿透几个小立方体.

（1）铁丝穿透1个小立方体可有三种不同情况.（如图1所示）其中A、B两种是穿过相对两面，A种平行于棱的方向穿过，B种斜着穿过；

C种则是穿过相邻两面.再进一步分析，若增加7个小立方体，搭成较大立方体时，这个小立方体相对两面中只能有一个面与其它小立方体相邻，也就是说只能考虑铁丝在一个方向上继续穿透其它小立方体.而这个小立方体相邻的两面可以分别与其它小立方体相邻，铁丝可以沿两个方向继续穿透其它小立方体.因此，C种情况是我们解答本题需要深入考虑的.（为了便于分析，将这个小立方体编为①号.）

（2）考虑铁丝扎进较大立方体时最多可以穿透几个小立方体.如图2所示，铁丝沿斜上方向可继续穿透②号小立方体，沿斜下方向可继续穿透③号、④号小立方体.因此，共可穿透4个小立方体.

　　（3）考虑铁丝扎进27个小立方体搭成的大立方体时，最多可以穿透几个小立方体.如图3所示，铁丝沿斜上方向可继续穿透⑤号立方体，沿斜下方向可以继续穿透⑥号、⑦号小立方体.因此，最多可以穿透7个小立方体.

[说明与探讨]本题意在考察空间观念和画图能力.若直接考虑，难度比较大.所以应采取从简单处人手，逐步深入分析的方法来解答.通过上述分析，不难发现这样一条规律（如下表所示）：

　　以前，我们研究过与此题分析方法基本相同的平面图形问题.如：

大正方形是由25个同样大小的小正方形拼接而成的.在大正方形上画一条直线，这条直线最多可以穿过几个小正方形？