正弦函数的图像和性质(公开课)精品课件优质PPT.ppt

正弦函数的图像和性质(公开课)精品课件优质PPT.ppt

《正弦函数的图像和性质(公开课)精品课件优质PPT.ppt》由会员分享，可在线阅读，更多相关《正弦函数的图像和性质(公开课)精品课件优质PPT.ppt（21页珍藏版）》请在冰豆网上搜索。

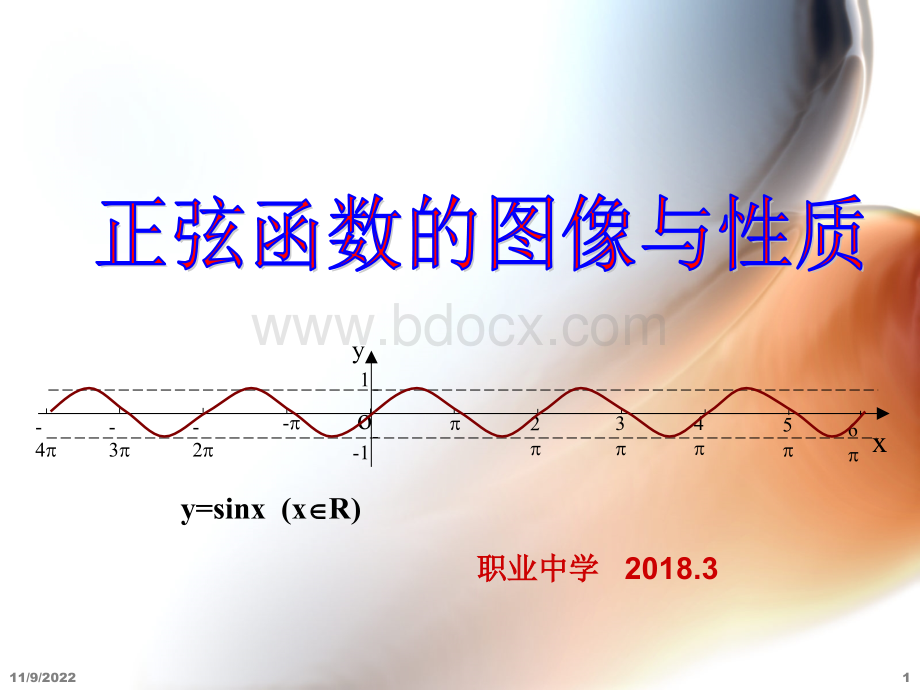
正弦函数y=y=sinxsinx定义域和值域定义域和值域11/9/20223思考：

观察正弦线变化范围思考：

观察正弦线变化范围,并总结并总结sinx的性质的性质.sinx最大为最大为1sinx最小为最小为111/9/20224例例2、设、设sinx=t-3，xR，求，求t的取值范围。

的取值范围。

例例1、下列各等式能否成立？

为什么？

、下列各等式能否成立？

（1）2sinx=3；

（2）sin2x=0.511/9/20225例例3求下列函数的最值，并求出相应求下列函数的最值，并求出相应的的x值。

值。

（1）y=2sinx

（2）y=sinx+2（3）y=sin2x11/9/20226思考：

思考：

y=sinx，xR的图象为什么会重复出现形的图象为什么会重复出现形状相同的曲线呢状相同的曲线呢?

sin（x+2k）=sinx（kZ）xy1-111/9/20227一般地，对于函数一般地，对于函数f（x），如果存在一个非），如果存在一个非零常数零常数T，使得定义域内的，使得定义域内的每一个每一个x值，都满值，都满足足f（x+T）=f（x），），那么函数那么函数f（x）就叫做）就叫做周期函数，非零常数周期函数，非零常数T叫做这个函数的周期。

叫做这个函数的周期。

性质二：

正弦函数性质二：

正弦函数y=y=sinxsinx周期性周期性11/9/20228对于一个周期函数对于一个周期函数f（x），如果在它的所有周），如果在它的所有周期中存在一个最小的正数，那么这个最小的期中存在一个最小的正数，那么这个最小的正数就叫做它的正数就叫做它的最小正周期最小正周期。

y=sinx的最小正周期的最小正周期T=2性质二：

正弦函数y=y=sinxsinx周期性周期性11/9/20229例例4求下列函数的周期：

求下列函数的周期：

11/9/202210正弦函数的单调性正弦函数的单调性y=sinx（xR）增增区间为区间为，其值从其值从-1增至增至1xyo-1234-2-31xsinx0-1010-1减区间为减区间为，其值从其值从1减至减至-1+2k,+2k,kZ+2k,+2k,kZ11/9/202211正弦函数正弦函数y=siny=sinx（xRx（xR）的图象的图象xy1-111/9/202212性质三：

正弦函数性质三：

正弦函数y=y=sinxsinx的单调性的单调性11/9/20221311/9/202214xy1-1因此正弦函数是奇函数因此正弦函数是奇函数11/9/2022151、正弦曲线关于原点（、正弦曲线关于原点（0，0）对称；

）对称；

正弦函数正弦函数f（x）=sinx为奇函数。

为奇函数。

正弦函数y=y=sinxsinx的对称性（奇偶性）的对称性（奇偶性）xyo-1234-2-312、正弦曲线的对称点、正弦曲线的对称点；

3、正弦曲线的对称轴、正弦曲线的对称轴11/9/202216B三三.课堂练习课堂练习11/9/202217CA11/9/202218C11/9/202219xy1-1性质一：

定义域和值域性质一：

定义域和值域性质三：

单调性性质三：

单调性性质二：

周期性性质二：

周期性性质四：

奇偶性性质四：

奇偶性定义域为定义域为R，值域为，值域为-1,1四、课堂小结四、课堂小结1、正弦曲线关于原点（、正弦曲线关于原点（0，0）对称；

2、正弦曲线的对称点、正弦曲线的对称点；

3、正弦曲线的对称轴、正弦曲线的对称轴11/9/202220五五.作业布置作业布置1.完成完成步步高步步高上对应的部上对应的部分。

分。

2.预习预习余弦函数余弦函数的内容。

的内容。

11/9/202221