空间几何体的三视图表面积与体积学案高考总复习热点训练Word格式文档下载.docx

空间几何体的三视图表面积与体积学案高考总复习热点训练Word格式文档下载.docx

《空间几何体的三视图表面积与体积学案高考总复习热点训练Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《空间几何体的三视图表面积与体积学案高考总复习热点训练Word格式文档下载.docx（18页珍藏版）》请在冰豆网上搜索。

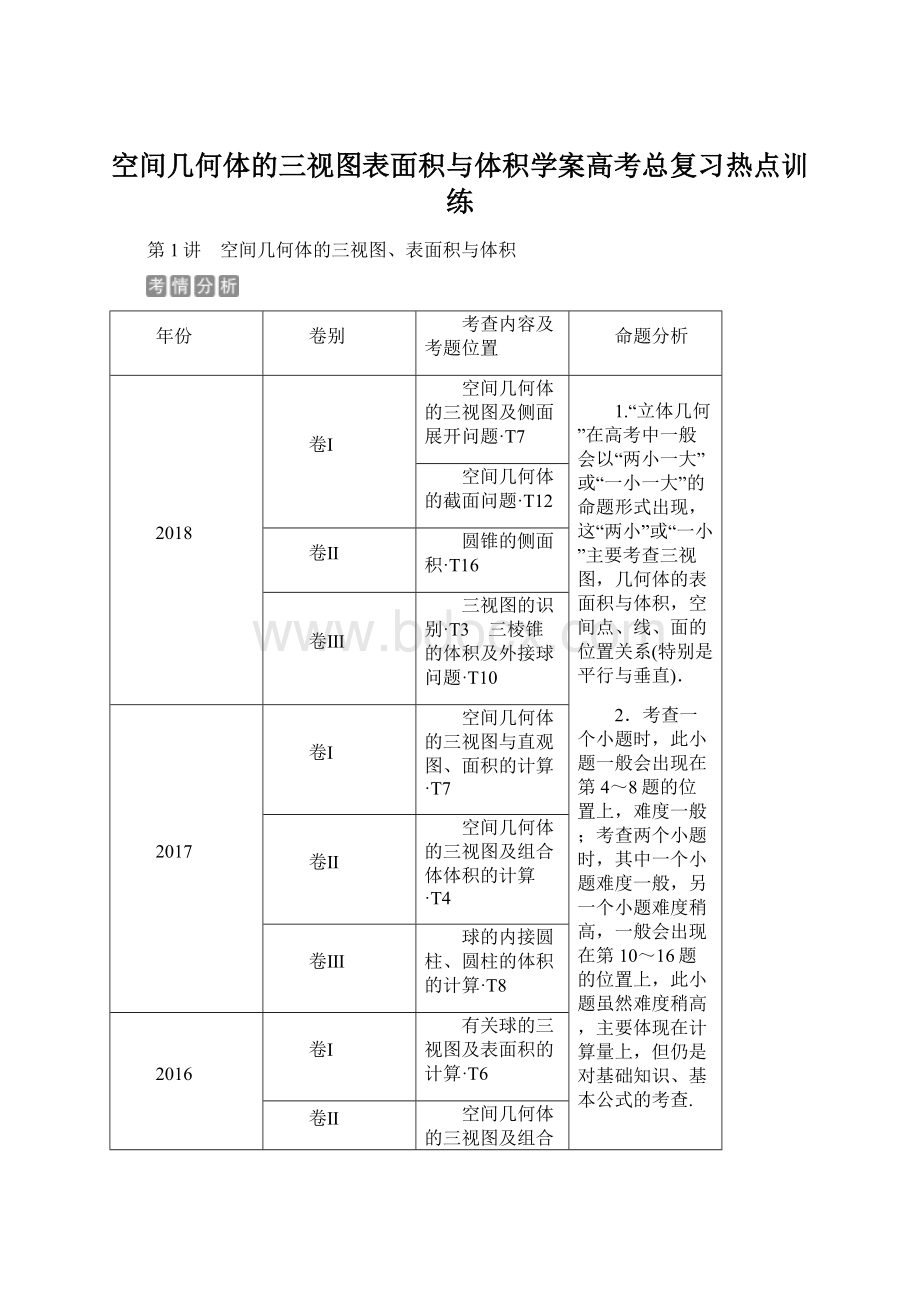
圆锥的侧面积·

T16

卷Ⅲ

三视图的识别·

T3　三棱锥的体积及外接球问题·

T10

2017

空间几何体的三视图与直观图、面积的计算·

空间几何体的三视图及组合体体积的计算·

T4

球的内接圆柱、圆柱的体积的计算·

T8

2016

有关球的三视图及表面积的计算·

T6

空间几何体的三视图及组合体表面积的计算·

T9

直三棱柱的体积最值问题·

　　　空间几何体的三视图（基础型）

一个物体的三视图的排列规则

俯视图放在正（主）视图的下面，长度与正（主）视图的长度一样，侧（左）视图放在正（主）视图的右面，高度与正（主）视图的高度一样，宽度与俯视图的宽度一样．即“长对正、高平齐、宽相等”．

由三视图还原到直观图的三个步骤

（1）根据俯视图确定几何体的底面．

（2）根据正（主）视图或侧（左）视图确定几何体的侧棱与侧面的特征，调整实线和虚线所对应的棱、面的位置．

（3）确定几何体的直观图形状．

[注意]　在读图或者画空间几何体的三视图时，应注意三视图中的实线和虚线．

[考法全练]

1．（2018·

高考全国卷Ⅲ）中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（　　）

解析：

选A.由题意知，在咬合时带卯眼的木构件中，从俯视方向看，榫头看不见，所以是虚线，结合榫头的位置知选A.

2．（2018·

高考全国卷Ⅰ）某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（　　）

A．2B．2

C．3D．2

选B.由三视图可知，该几何体为如图①所示的圆柱，该圆柱的高为2，底面周长为16.画出该圆柱的侧面展开图，如图②所示，连接MN，则MS＝2，SN＝4，则从M到N的路径中，最短路径的长度为＝＝2.故选B.

3．把边长为1的正方形ABCD沿对角线BD折起，使得平面ABD⊥平面CBD，形成的三棱锥CABD的正视图与俯视图如图所示，则侧视图的面积为（　　）

A.B.

C.D.

选D.由三棱锥CABD的正视图、俯视图得三棱锥CABD的侧视图为直角边长是的等腰直角三角形，如图所示，所以三棱锥CABD的侧视图的面积为，故选D.

4．（2018·

长春质量监测

（二））如图，网格纸上小正方形的边长为1，粗线条画出的是一个三棱锥的三视图，则该三棱锥中最长棱的长度为（　　）

A．2B.

C．2D．3

选D.如图，三棱锥ABCD即为所求几何体，根据题设条件，知辅助的正方体棱长为2，CD＝1，BD＝2，BC＝，AC＝2，AB＝3，AD＝，则最长棱为AB，长度为3.

5．（2018·

石家庄质量检测

（一））如图，网格纸上的小正方形的边长为1，粗线表示的是某三棱锥的三视图，则该三棱锥的四个面中，最小面的面积是（　　）

A．2B．2

C．2D.

选C.在正方体中还原该几何体，如图中三棱锥DABC所示，其中正方体的棱长为2，则S△ABC＝2，S△DBC＝2，S△ADB＝2，S△ADC＝2，故该三棱锥的四个面中，最小面的面积是2，选C.

　　　空间几何体的表面积和体积（综合型）

柱体、锥体、台体的侧面积公式

（1）S柱侧＝ch（c为底面周长，h为高）．

（2）S锥侧＝ch′（c为底面周长，h′为斜高）．

（3）S台侧＝（c＋c′）h′（c′，c分别为上下底面的周长，h′为斜高）．

柱体、锥体、台体的体积公式

（1）V柱体＝Sh（S为底面面积，h为高）．

（2）V锥体＝Sh（S为底面面积，h为高）．

（3）V台＝（S＋＋S′）h（S，S′分别为上下底面面积，h为高）（不要求记忆）．

[典型例题]

命题角度一　空间几何体的表面积

（1）（2018·

潍坊模拟）某几何体的三视图如图所示，则该几何体的表面积为（　　）

A．4＋2　　　　　　B．4＋4

C．6＋2D．6＋4

（2）（2018·

合肥第一次质量检测）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（　　）

A．5π＋18B．6π＋18

C．8π＋6D．10π＋6

【解析】　

（1）由三视图还原几何体的直观图如图所示，易知BC⊥平面PAC，又PC⊂平面PAC，所以BC⊥PC，又AP＝AC＝BC＝2，所以PC＝＝2，又AB＝2，所以S△PBC＝S△PAB＝×

2×

2＝2，S△ABC＝S△PAC＝×

2＝2，所以该几何体的表面积为4＋4.

（2）由三视图可知该几何体是由一个半圆柱和两个半球构成的，故该几何体的表面积为2×

×

4π×

12＋2×

π×

3＋×

2π×

1×

3＝8π＋6.

【答案】　

（1）B　

（2）C

求几何体的表面积的方法

（1）求表面积问题的基本思路是将立体几何问题转化为平面几何问题，即空间图形平面化，这是解决立体几何的主要出发点．

（2）求不规则几何体的表面积时，通常将所给几何体分割成基本的柱、锥、台体，先求这些柱、锥、台体的表面积，再通过求和或作差得几何体的表面积．　

命题角度二　空间几何体的体积

武汉调研）某几何体的三视图如图所示，则该几何体的体积为（　　）

高考全国卷Ⅱ）已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°

.若△SAB的面积为8，则该圆锥的体积为________．

【解析】　

（1）由三视图知，该几何体是在长、宽、高分别为2，1，1的长方体中，截去一个三棱柱AA1D1BB1C1和一个三棱锥CBC1D后剩下的几何体，即如图所示的四棱锥DABC1D1，四棱锥DABC1D1的底面积为S四边形ABC1D1＝2×

＝2，高h＝，其体积V＝S四边形ABC1D1h＝×

＝.故选D.

（2）由题意画出图形，如图，设AC是底面圆O的直径，连接SO，则SO是圆锥的高．设圆锥的母线长为l，则由SA⊥SB，△SAB的面积为8，得l2＝8，得l＝4.在Rt△ASO中，由题意知∠SAO＝30°

，所以SO＝l＝2，AO＝l＝2.

故该圆锥的体积V＝π×

AO2×

SO＝π×

（2）2×

2＝8π.

【答案】　

（1）D　

（2）8π

求空间几何体体积的常用方法

（1）公式法：

直接根据相关的体积公式计算．

（2）等积法：

根据体积计算公式，通过转换空间几何体的底面和高使得体积计算更容易，或是求出一些体积比等．

（3）割补法：

把不能直接计算体积的空间几何体进行适当分割或补形，转化为易计算体积的几何体．　

[对点训练]

洛阳第一次统考）一个几何体的三视图如图所示，图中的三个正方形的边长均为2，则该几何体的体积为（　　）

A．8－B．4－

C．8－D．4－

选A.由三视图可得该几何体的直观图如图所示，该几何体是一个棱长为2的正方体上、下各挖去一个底面半径为1，高为1的圆锥后剩余的部分，其体积为23－2×

12×

1＝8－.故选A.

唐山模拟）如图，网格纸上小正方形的边长为1，粗线画的是一个几何体的三视图，则该几何体的体积为（　　）

A．3B.

C．7D.

选B.由题中的三视图可得，该几何体是由一个长方体切去一个三棱锥所得的几何体，长方体的长，宽，高分别为2，1，2，体积为4，切去的三棱锥的体积为，故该几何体的体积V＝4－＝.故选B.

　　　多面体与球（综合型）

命题角度一　外接球

（2018·

南宁模拟）三棱锥PABC中，△ABC为等边三角形，PA＝PB＝PC＝3，PA⊥PB，三棱锥PABC的外接球的体积为（　　）

A.πB.π

C．27πD．27π

【解析】　因为三棱锥PABC中，△ABC为等边三角形，PA＝PB＝PC＝3，所以△PAB≌△PBC≌△PAC.因为PA⊥PB，所以PA⊥PC，PC⊥PB.以PA，PB，PC为过同一顶点的三条棱作正方体（如图所示），则正方体的外接球同时也是三棱锥PABC的外接球．因为正方体的体对角线长为＝3，所以其外接球半径R＝.因此三棱锥PABC的外接球的体积V＝×

＝π，故选B.

【答案】　B

解决多面体的外接球问题，关键是确定球心的位置，方法是先选择多面体中的一面，确定此面外接圆的圆心，再过圆心作垂直此面的垂线，则球心一定在此垂线上，最后根据其他顶点确定球心的准确位置．对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置．　

命题角度二　内切球

已知一个平放的各棱长为4的三棱锥内有一个小球O（重量忽略不计），现从该三棱锥顶端向内注水，小球慢慢上浮，当注入的水的体积是该三棱锥体积的时，小球与该三棱锥各侧面均相切（与水面也相切），则小球的表面积等于（　　）

【解析】　当注入水的体积是该三棱锥体积的时，设水面上方的小三棱锥的棱长为x（各棱长都相等），依题意，＝，得x＝2.易得小三棱锥的高为，设小球半径为r，则S底面·

＝4·

·

S底面·

r，得r＝，故小球的表面积S＝4πr2＝.故选C.

【答案】　C

求解多面体的内切球的问题，一般是将多面体分割为以球心为顶点，多面体的各面为底面的棱锥，利用多面体的体积等于各棱锥的体积之和求内切球的半径．　

命题角度三　与球有关的最值问题

高考全国卷Ⅲ）设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为9，则三棱锥DABC体积的最大值为（　　）

A．12B．18

C．24D．54

【解析】　如图，E是AC中点，M是△ABC的重心，O为球心，连接BE，OM，OD，BO.因为S△ABC＝AB2＝9，所以AB＝6，BM＝BE＝＝2.易知OM⊥平面ABC，所以在Rt△OBM中，OM＝＝2，所以当D，O，M三点共线且DM＝OD＋OM时，三棱锥DABC的体积取得最大值，且最大值Vmax＝S△ABC×

（4＋OM）＝×

9×

6＝18.故选B.

多面体与球有关的最值问题，主要有三种：

一是多面体确定的情况下球的最值问题，二是球的半径确定的情况下与多面体有关的最值问题；

三是多面体与球均确定的情况下，截面的最值问题．　

福州模拟）已知圆锥的高为3，底面半径为，若该圆锥的顶点与底面的圆周都在同一个球面上，则这个球的体积等于（　　）

C．16πD．32π

选B.设该圆锥的外接球的半径为R，依题意得，R2＝（3－R）2＋（）2，解得R＝2，所以所求球的体积V＝πR3＝π×

23＝π，故选B.

洛阳第一次联考）已知球O与棱长为4的正四面