Cannon乘法的MPI实现Word文件下载.docx

Cannon乘法的MPI实现Word文件下载.docx

《Cannon乘法的MPI实现Word文件下载.docx》由会员分享，可在线阅读，更多相关《Cannon乘法的MPI实现Word文件下载.docx（17页珍藏版）》请在冰豆网上搜索。

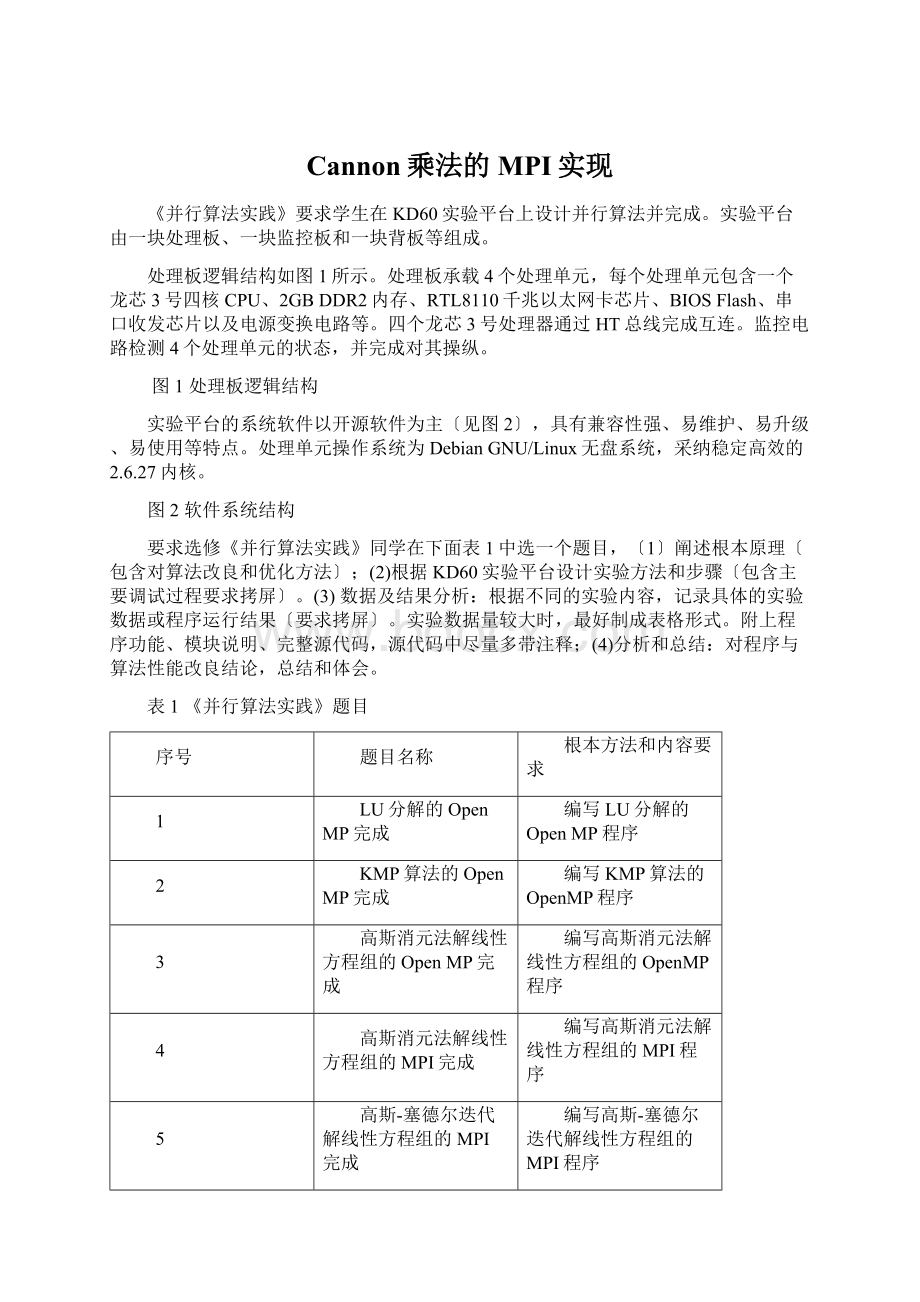
序号

题目名称

根本方法和内容要求

1

LU分解的OpenMP完成

编写LU分解的OpenMP程序

2

KMP算法的OpenMP完成

编写KMP算法的OpenMP程序

3

高斯消元法解线性方程组的OpenMP完成

编写高斯消元法解线性方程组的OpenMP程序

4

高斯消元法解线性方程组的MPI完成

编写高斯消元法解线性方程组的MPI程序

5

高斯-塞德尔迭代解线性方程组的MPI完成

编写高斯-塞德尔迭代解线性方程组的MPI程序

6

Cannon乘法的MPI完成

编写Cannon乘法的MPI程序

7

LU分解的MPI完成

编写LU分解的MPI程序

8

随机串匹配算法的MPI完成

编写随机串匹配算法的MPI程序

9

单源最短路径Dijkstra算法的MPI完成

编写单源最短路径Dijkstra算法的MPI程序

10

快速排序算法的MPI完成

编写快速排序算法的MPI程序

11

KMP串匹配的MPI完成

编写KMP串匹配算法的MPI程序

Cannon乘法的MPI完成及性能分析

摘要：

cannon算法是矩阵的并行乘法，属于数值并行算法MPI编程完成一篇，其中关于数值并行算法MPI编程由于要处理的数据量庞大，程序循环次数多，对于串行而言，处理时间将非常长，将其并行化非常必要。

本文将矩阵数据进行棋盘划分成多个子矩阵，再分别指派给多个处理器，使个处理器并行运算。

关键字：

cannon乘法并行计算数据划分

一、Cannon乘法的MPI完成根本原理

Cannon乘法属于数值并行算法MPI编程完成一篇，其中关于数值并行算法MPI编程由于要处理的数据量庞大，程序循环次数多，对于串行而言，处理时间将非常长，使其并行化的一般方法有：

1〕数据相关分析2〕数据划分和处理器指派3〕循环重构

对原有程序并行化，首先要分析计算程序中全部语句间的依赖关系，这称之为相关分析。

本工程Cannon乘法的mpi完成，是矩阵运算，阶往往都很高，而且行列之间数据依赖关系也不强，所以就对矩阵进行划分，然后指派给不同的处理器进行处理。

最常用的矩阵划分有带状划分和块状划分。

1．带状划分方法

带状划分又叫行列划分，就是将矩阵整行或整列地分成假设干组，各组指派给一个处理器。

也可以将假设干行或列指派给一个处理器，而且这些行和列可以是连续的，也可以是等间距的，前者称为块带状的，后者称为循环带状的。

2.块状划分方法

块状划分又叫棋盘划分，就是将矩阵划分成假设干个子矩阵，每个子矩阵指派给一个处理器，此时任意处理器均不含整行或整列。

和带状划分类似，棋盘划分也可分为块棋盘划分和循环棋盘划分。

棋盘划分比带状划分可开发更高的并行度，Cannon乘法的mpi完成也正是基于棋盘划分的并行完成。

循环重构是指在数据分解之后，相应地将串行程序循环局部进行重构，以完成这种划分所确定的并行计算，主要方法有1〕循环交换2〕拉伸法3〕分裂法4〕轮转法5〕并列法在三种程序并行化的方法中，数据相关分析和循环重构目的都是挖掘语句间的并行性，而数据划分和处理器指派则重在策略，宏观上挖掘并行性。

Cannon算法是一种存储有效的算法，设矩阵和相乘。

为了使两矩阵下标满足相乘的要求，和带状的并行分块乘法不同，不是仅仅让B矩阵的各列块循环移动，而是有目的地让A的各行块以及B的各列块皆施行循环移位，从而完成对C的子块的计算。

将矩阵A和B分成p个方块Aij和Bij，，每块大小为，并将它们分配给个处理器。

开始时处理器Pij存放块Aij和Bij，并负责计算块Cij，然后算法开始执行：

⑴将块Aij向左循环移动i步；

将块Bij向上循环移动j步；

⑵Pij执行乘加运算后将块Aij向左循环移动1步，块Bij向上循环移动1步；

⑶重复第⑵步，总共执行次乘加运算和次块Aij和Bij的循环单步移位。

二、Cannon乘法的MPI完成内容和步骤

实验涉及内容主要有：

1〕数据划分和指派处理器

最常用的矩阵数据划分有带状划分和块状划分。

设有P个处理器，将矩阵A和B分成p个方块Aij和Bij，，每块大小为，并将它们分配给个处理器。

2〕子矩阵的循环移动

处理器Pij存放块Aij和Bij，并负责计算块Cij，在使A矩阵的左右循环移动和B矩阵的上下循环移动时，为了防止在通信过程中发生死锁，奇数号及偶数号处理器的收发顺序被错开，使偶数号处理器先发送后接收；

而奇数号处理器先将子矩阵块存于缓冲区Buffer中，然后接收编号在其后面的处理器所发送的子矩阵块，最后再将缓冲区中子矩阵块发送给编号在其前面的处理器。

根本算法如下：

Begin

（1）if（j=0）then/*最左端的子块*/

（1.1）将所存的A的子块发送到同行最右端子块所在的处理器中

（1.2）接收其右邻处理器中发来的A的子块

endif

（2）if（（j=sqrt（p）-1）and（jmod2=0））then/*最右端子块处理器且块列号为偶数*/

（2.1）将所存的A的子块发送到其左邻处理器中

（2.2）接收其同行最左端子块所在的处理器发来的A的子块

（3）if（（j=sqrt（p）-1）and（jmod2≠0））then/*最右端子块处理器且块列号为奇数*/

（3.1）将所存的A的子块在缓冲区buffer中做备份

（3.2）接收其同行最左端子块所在的处理器发来的A的子块

（3.3）将在缓冲区buffer中所存的A的子块发送到其左邻处理器中

（4）if（（j≠sqrt（p）-1）and（jmod2=0）and（j≠0））then/*其余的偶数号处理器*/

（4.1）将所存的A的子块发送到其左邻处理器中

（4.2）接收其右邻处理器中发来的A的子块

（5）if（（j≠sqrt（p）-1）and（jmod2=1）and（j≠0））then/*其余的奇数号处理器*/

（5.1）将所存的A的子块在缓冲区buffer中做备份

（5.2）接收其右邻处理器中发来的A的子块

（5.3）将在缓冲区buffer中所存的A的子块发送到其左邻处理器中

End

实验步骤

1）登陆KD-60

图2.1KD-60登陆界面

2）转至node80节点，上传程序

输入命令：

sshloongson@node80和密码进入图界面

图2.2转到节点80的界面

再命令vim，进入vim编辑器参加程序,保存为cannon.c

3）编译程序

mpicccannon.c–ocannon–lm

在目录中查看，已成功。

如下列图

图2.3将程序保存并编译后界面

4）运行程序

输入：

mpirun–np4cannon4,其中第一个4是指定的处理器个数，第二个4是产生随机矩阵的维数，这两个参数在实验过程中可以调整，但要求第一个参数即处理器的个数必须是一个数的平方数。

输出：

图2.4cannon乘法运行结果

图2.4并行程序运行界面两个参数都是4，分别输出两个随机矩阵和矩阵的乘积

三、数据及结果

1.下面列出了两组数据，分别是用一个处理器进行串行运算和四个处理器进行并行运算矩阵维数为200的计算时间比拟。

四个处理器处理阶数为200的矩阵相乘时，所花时间为：

。

单个处理器处理阶数为200的矩阵相乘时，所花时间为：

3.727210秒。

如图3.1和图3.2所示。

图3.1四个处理器并行执行结果图

图3.2单个处理器串行执行结果图

附：

1.程序模块伪代码：

An×

n，Bn×

n

Cn×

对全部处理器my_rank（my_rank=0,…,p-1）同时执行如下的算法:

（1）计算子块的行号i=my_rank/sqrt（p）

计算子块的列号j=my_rankmodsqrt（p）

（2）fork=0to-1do

if（i>

k）thenLeftmoveonestep（a）endif/*a循环左移至同行相邻处理器中*/

if（j>

k）thenUpmoveonestep（b）endif/*b循环上移至同列相邻处理器中*/

endfor

（3）fori=0tom-1do

forj=0tom-1do

c[i,j]=0

endfor

（4）fork=0to-1do

fori=0tom-1do

fork1=0tom-1do

c[i,j]=c[i,j]+a[i,k1]*b[k1,j]

Leftmoveonestep（a）/*子块a循环左移至同行相邻的处理器中*/

Upmoveonestep（b）/*子块b循环上移至同列相邻的处理器中*/

Leftmoveonestep（a）见实验内容处

#include<

stdlib.h>

string.h>

mpi.h>

time.h>

stdio.h>

math.h>

/*全局变量声明*/

float**A,**B,**C;

/*总矩阵,C=A*B*/

float*a,*b,*c,*tmp_a,*tmp_b;

/*a、b、c表分块，tmp_a、tmp_b表缓冲区*/

intdg,dl,dl2,p,sp;

/*dg:

总矩阵维数;

dl:

矩阵块维数;

dl2=dl*dl;

p:

处理器个数;

sp＝sqrt（p）*/

intmy_rank,my_row,my_col;

/*my_rank:

处理器ID;

（my_row,my_col）:

处理器逻辑阵列坐标*/

MPI_Statusstatus;

floatstarttime;

floattime1;

/*

*函数名:

get_index

*功能：

处理器逻辑阵列坐标至rank号的转换

*输入：

坐标、逻辑