陕西省中考数学试题及答案Word文档格式.docx

陕西省中考数学试题及答案Word文档格式.docx

《陕西省中考数学试题及答案Word文档格式.docx》由会员分享，可在线阅读，更多相关《陕西省中考数学试题及答案Word文档格式.docx（18页珍藏版）》请在冰豆网上搜索。

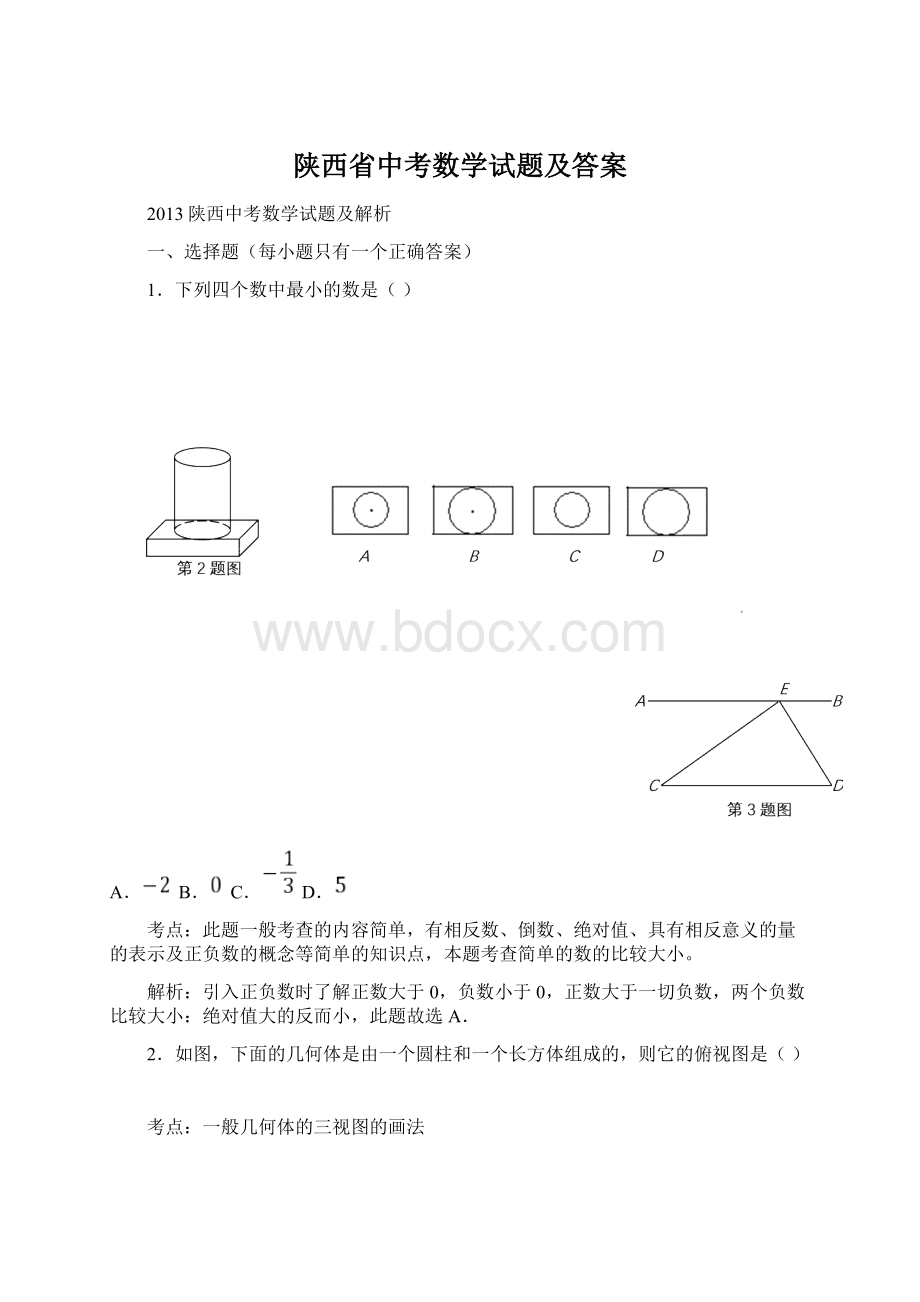
平行线的性质应用与互余的定义。

此类题主要考查学生们的平面几何的性质应用的能力，

一般考查常见较为简单的两直线平行而同位角和内错角相等

的应用，而问题的设置也是求角度或者是找角的关系。

因为AB∥CD，所以∠D=∠BED，因为∠CED=90°

所以∠BED=180°

-90°

-35°

=55°

，此题故选B

4．不等式组的解集为（）

不等式的解法及不等式组的解集的选取。

此题一般考不等式组或者是一元一次方程的应用等简单的计算能力考查。

易错就是不等式的性质3，乘除负数时不等号的方向应改变。

解集的选取应尊循：

“大大取大；

小小取小；

大小小大取中间；

大大小小取不了”的原则。

第1个不等式解得：

；

第2个不等式解得：

因此不等式组的解集为：

此题故选A

5．我省某市五月份第二周连续七天的空气质量指数分别为：

111，96，47，68，70，77，105，则这七天空气质量指数的平均数是（）

A．B．77C．82

此题一般考查统三个计量（平均数，中位数、众数）的选择和计算。

年年的必考的知识点。

；

故选C．

6．如果一个正比例函数的图象经过不同象限的两点A（2,m），B（n，３），那么一定有（）

A．m>

0，n>

0B．m>

0，n<

0C．m<

0D．m<

一般考查的是一次函数或者反比例函数的图象性质及待定系数法求函数的解析式。

因为A，B是不同象限的点，而正比例函数的图象要不在一、三象限或在二、四象限，由点A与点B的横纵坐标可以知：

点A与点B在一、三象限时：

横纵坐标的符号应一致，显然此题不可能，点A与点B在二、四象限：

点A在四象限得m<

0，点B在二象限得n<

0,故选D．（另解：

就有两种情况一、三或二、四象限，代入特值即可判定）

7．如图，在四边形中，对角线AB=AD，CB=CD，

若连接AC、BD相交于点O，则图中全等三角形共有（）

A．1对B．2对C．3对D．4对

全等三角形的判定。

AB=AD，CB=CD，AC公用，因此△ABC≌△ADC（SSS），

所以BAO=DAO，BCO=DCO，

所以△BAO≌△DAO（SAS），

△BCO≌△DCO（SAS），故选C

8．根据下表中一次函数的自变量x与函数y的对应值，可得p的值为（）

x

－2

1

y

3

p

A．1B．－1C．3D．－3

待定系数法求一次函数的解析式及由自变量的值确定对应的函数值。

设y=kx+b，将表格中的对应的x,y的值代入得二元一次方程组，解方程组得k,b的值，回代x=0时，对应的y的值即可。

设y=kx+b，解得：

k=－1，b=1,所以所以y=－x+1,当x=0时，得y=1,故选A．

9.如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC是，连接BM、DN，若四边形MBND是菱形，则等于（）

矩形的性质及菱形的性质应用。

矩形的性质应用较为常见的就是转化成直角三角形来解决问题，菱形的性质应用较常见的是四条边相等或者对角线的性质应用。

此题中求的是线段的比值，所以在解决过程中取特殊值法较为简单。

设AB=1，则AD=2，因为四边形MBND是菱形，所以MB=MD，又因为矩形ABCD，所以A=90°

，设AM=x,则MB=2-x，由勾股定理得：

AB2+AM2=MB2，所以x2+12=（2-x）2解得：

，所以MD=，，故选C．

10.已知两点均在抛物线上，点是该抛物线的顶点，若，则的取值范围是（）

二次函数图象性质的应用及对称性的考查。

由点是该抛物线的顶点，且，所以为函数的最小值，即得出抛物线的开口向上，因为，所以得出点A、B可能在对称轴的两侧或者是在对称轴的左侧，当在对称轴的左侧时，y随x的增大而减小，因此>

3，当在对称轴的两侧时，点B距离对称轴的距离小于点A到对称轴的距离，即得-（-5）>

3-,解得，综上所得：

，故选B

第Ⅱ卷（非选择题共90分）

二、填空题（共6小题，每小题3分，计18分）

11．计算：

．

本题经常实数的简单计算、特殊角的三角函数值及零（负）指数幂及绝对值的计算。

原式=

12.一元二次方程的根是．

一元二次方程的解法。

四种解一元二次方程的解法即：

直接开平方法，配方法，公式法，因式分解法。

此12题的位置一般是简单的题，因此注意识别使用简单的方法进行求解。

由得，，解得x1=0,x2=3

13．请从以下两个小题中任选一个作答，若多选，则按所选的第一题计分．

A．在平面直角坐标第中，线段AB的两个端点的坐标分别为，将线段AB经过平移后得到线段，若点A的对应点为，则点B的对应点的坐标是．

点的平移与坐标之间的关系。

点A与对应，从坐标来看是将点A向右平移5个单位后再向上平移1个单位得到，所以点B的坐标也是向右平移5个单位后再向上平移1个单位得

B．比较大小：

（填“>

”，“=”，“<

”）．

科学计算器的使用：

数的开方及三角函数值。

按键顺序：

易得填“>

”

14．如图，四边形ABCD的对角线AC、BD相交于点O，且BD平分AC，若BD=8，AC=6，∠BOC=120°

，则四边形ABCD的面积为.（结果保留根号）

三角形面积的求法及特殊角的应用。

BD平分AC，所以OA=OC=3，因为∠BOC=120°

，

所以∠DOC=∠A0B=60°

，过C作CH⊥BD于H，

过A作AG⊥BD于G，在△CHO中，∠C0H=60°

OC=3，所以CH=，同理：

AG=，

所以四边形ABCD的面积=。

15．如果一个正比例函数的图象与一个反比例函数的图象交，那么值为.

正比例函数与反比例函数的交点的对称性的考查。

因为A，B在反比例函数上，所以，我们知道正比例函数与反比例函数的交点坐标关于原点成中心对称，因此中有，所以

16．如图，AB是⊙O的一条弦，点C是⊙O上一动点，

且∠ACB=30°

，点E、F分别是AC、BC的中点，

直线EF与⊙O交于G、H两点，若⊙O的半径为7，

则GE+FH的最大值为．

此题一般考查的是与圆有关的计算，考查有垂径定理、相交弦定理、圆心角与圆周角的关系，及扇形的面积及弧长的计算公式等知识点。

本题考查圆心角与圆周角的关系应用，中位线及最值问题。

连接OA，OB，

因为∠ACB=30°

，所以∠AOB=60°

，所以OA=OB=AB=7，因为E、F中AC、BC的中点，

所以EF==，因为GE+FH=GH－EF，要使GE+FH最大，而EF为定值，所以GH取最大值时GE+FH有最大值，所以当GH为直径时，GE+FH的最大值为=

三、解答题（共9小题，计72分．解答应写过程）

17．（本题满分5分）

解分式方程：

．

解分式方程，解题步骤是

（1）对分子分母分解因式，

（2）去分母化分式方程为整式方程，（3）检验；

（此题陕西命题的规律一般是分式化简与分式方程轮流考。

）。

去分母得：

整理得：

解得：

经检验得，是原分式方程的根.

18．（本题满分6分）

如图，∠AOB=90°

，OA=0B，直线经过点O,分别过A、B两点作AC⊥交于点C，BD⊥交于点D.

求证：

AD=OD.

互余的性质应用、垂直的性质及三角形全等的判定。

∵∠AOB=90°

∴∠AOC+∠BOD=90°

∵AC⊥，BD⊥∴∠ACO=∠BDO=90°

∴∠A+∠AOC=90°

∴∠A=∠BOD

又∵OA=OB∴△AOC≌△OBD（AAS）

∴AC=OD

19．（本题满分7分）

我省教育厅下发了《在全省中小学幼儿园广泛开展节约教育的通知》，通知中要求各学校全面持续开展“光盘行动”.

某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度（程度分为：

“A-了解很多”，“B-了解较多”，“C-了解较少”，“D-不了解”），对本市一所中学的学生进行了抽样调查，我们将这次调查的结果绘制了以下两幅统计图.根据以上信息，解答下列问题：

（1）本次抽样调查了多少名学生？

（2）补全两幅统计图；

（3）若该中学共有1800名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较多”的有多少名？

条形统计图，扇形统计图；

此题陕西中考形式，难度与考点相对稳定。

此题考查的是统计思想，从统计图表中读取信息，条形统计图能得知个体的数目，扇形统计图能得出个体与总体的百分比。

从而并能做出正确的判断。

（1）抽样调查的学生人数为：

36÷

30%=120（名）

（2）B的人数：

120×

45%=54（名）

C的百分比：

D的百分比：

补全统计图如图所示；

（3）对“节约教育”内容“了解较多”的学生人数为：

1800×

45%=810（名）

20．（本题满分8分）

一天晚上，李明和张龙利用灯光下的影子来测量一路灯D的高度，如图，当李明走到点A处时，张龙测得李明直立身高AM与其影子长AE正好相等，接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB，并测得AB=1.25m。

已知李明直立时的身高为1.75m，求路灯的高CD的长.（结果精确到0.1m）

此题考查稳定，就是考查解直角三角形，或者考查的是相似三角形的应用测量高度，宽度等线段的长度的具体计算，将问题转换成方程（组）来求解，经常设置的具体的实际情景得到与测量相关的计算；

本题考查的是典型的测量问题之中心投影下的测量，而此问题设置基本上就是应用相似的性质来将实际问题转化成数学问题来解决，

解：

如图，设CD长为m∵AM⊥EC，CD⊥EC，BN⊥EC，EA=MA

∴MA∥CD，BN∥CD，∴EC=CD=，∴△ABN∽△ACD∴

即解得

所以路灯高CD约为6.1米

21．（本题满分8分）

“五一节“期间，申老师一家自驾游去了离家170千米的某地，下面是分们离家的距离（千米）与汽车行驶时间（小时）之间的函数图象。

（1）求他们出发半小时时，离家多少千米？

（2）求出AB段图象的函数表达式

（3）他们出发2小时时，离目的地还有多少千米？

此题考题与考点相对稳定，就是考查一次函数的应用及一次函数的增减性的判定，也有可能考查一元一次不等式组的应用及方案问题。

此题主要是将实际问题转化为函数的问题来解决，利用待定系数法来确定一次函数的表达式，给出自变量的值来求出相应的函数值。

（1）由图象可设OA段图象的函数表达式为y=kx

当x=时，y=90；

所以：

=90