高中数学必修二知识点总结Word文档格式.doc

高中数学必修二知识点总结Word文档格式.doc

《高中数学必修二知识点总结Word文档格式.doc》由会员分享，可在线阅读，更多相关《高中数学必修二知识点总结Word文档格式.doc（10页珍藏版）》请在冰豆网上搜索。

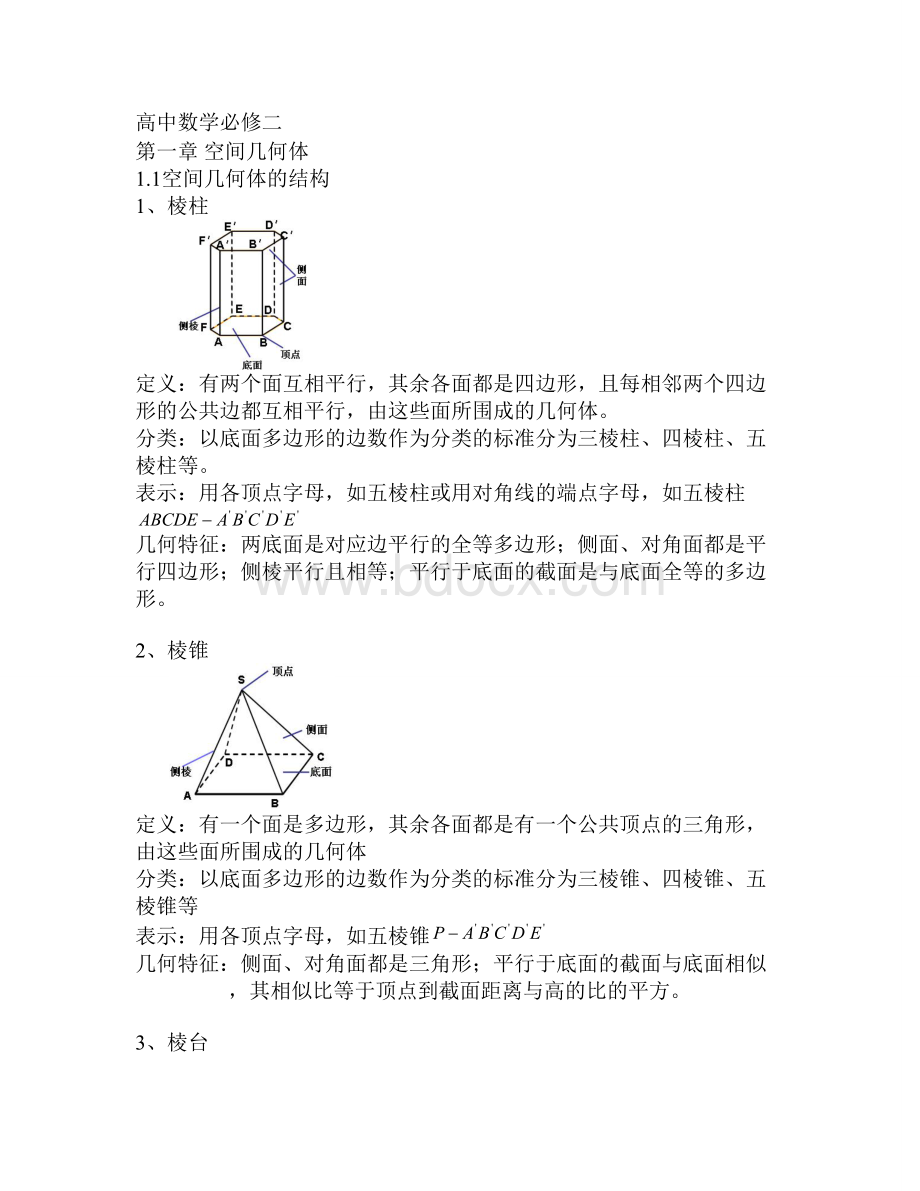
C'

D'

①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点

4、圆柱

以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体

①底面是全等的圆；

②母线与轴平行；

③轴与底面圆的半径垂直；

④侧面展开图是一个矩形。

5、圆锥

以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体

①底面是一个圆；

②母线交于圆锥的顶点；

③侧面展开图是一个扇形。

6、圆台

用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分

①上下底面是两个圆；

②侧面母线交于原圆锥的顶点；

③侧面展开图是一个弓形。

球体

以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体

①球的截面是圆；

②球面上任意一点到球心的距离等于半径。

※空间几何体的结构特征：

面（侧面、上底面、下底面）、棱、顶点、轴

1.2空间几何体的三视图和直观图

1、中心投影与平行投影

中心投影：

把光由一点向外散射形成的投影叫做中心投影。

平行投影：

在一束平行光照射下形成的投影叫做平行投影。

2、三视图

正视图：

从前往后

侧视图：

从左往右

俯视图：

从上往下

画三视图的原则：

长对齐、高对齐、宽相等

3、直观图：

斜二测画法

斜二测画法的步骤：

（1）.平行于坐标轴的线依然平行于坐标轴；

（2）.平行于y轴的线长度变半，平行于x，z轴的线长度不变；

（3）.画法要写好。

用斜二测画法画出长方体的步骤：

（1）画轴

（2）画底面（3）画侧棱（4）成图

1.3空间几何体的表面积与体积

（1）几何体的表面积为几何体各个面的面积的和。

（2）特殊几何体表面积公式（c为底面周长，h为高，为斜高，l为母线）

（3）柱体、锥体、台体的体积公式

（4）球体的表面积和体积公式：

V=；

S=

第二章点、直线、平面之间的位置关系

2.1空间点、直线、平面之间的位置关系

平面：

公理1：

如果一条直线上的两点在一个平面内，那么这条直线在

此平面内。

公理2：

过不在一条直线上的三点，有且只有一个平面

公理3：

如果两个不重合的平面有一个公共点，那么它们有且只

只有一条过改点的公共直线

‚线线关系：

1空间的两条直线有如下三种关系：

共面直线

相交直线：

同一平面内，有且只有一个公共点；

平行直线：

同一平面内，没有公共点；

异面直线：

不同在任何一个平面内，没有公共点。

公理4：

平行于同一条直线的两条直线互相平行。

符号表示为：

设a、b、c是三条直线

=>

a∥c

a∥b

c∥b

强调：

公理4实质上是说平行具有传递性，在平面、空间这个性质都

适用。

公理4作用：

判断空间两条直线平行的依据

ƒ线面位置关系

（1）直线在平面内——有无数个公共点

（2）直线与平面相交——有且只有一个公共点

（3）直线在平面平行——没有公共点

指出：

直线与平面相交或平行的情况统称为直线在平面外，可用aα来表示

aαa∩α=Aa∥α

4、面面关系

平行——没有公共点；

α∥β

相交——有一条公共直线。

α∩β＝b

2.2直线、平面平行的判定及其性质

1、线面平行判定

定理：

平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行，符号表示：

作用：

直线与平面的判定定理

2、面面平行

一个平面内的两条相交直线与另一平面平行，则这两个平面平行，

证面面平行

2.3直线、平面垂直的判定及其性质

1、线面垂直

一条直线与一个平面内的两条直线都垂直，则该直线与此平面垂直。

证线面垂直

线面角：

平面的一条斜线和它在平面上的射影所成的锐角。

※在解题时，注意挖掘题设中两个主要信息：

（1）斜线上一点到面的垂线；

（2）过斜线上的一点或过斜线的平面与已知面垂直，由面面垂直性质易得垂线。

2、面面垂直

（1）定理：

一个平面过另一个平面的垂线，则这两个平面垂直。

证面面垂直

（2）二面角：

从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，这两个半平面叫做二面角的面。

（3）二面角的平面角：

以二面角的棱上任意一点为顶点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫二面角的平面角。

（4）直二面角：

平面角是直角的二面角叫直二面角。

两相交平面如果所组成的二面角是直二面角，那么这两个平面垂直；

反过来，如果两个平面垂直，那么所成的二面角为直二面角

（5）求二面角的方法

定义法：

在棱上选择有关点，过这个点分别在两个面内作垂直于棱的射线得到平面角

‚垂面法：

已知二面角内一点到两个面的垂线时，过两垂线作平面两个面的交线所成的角为二面角的平面角

3、垂直关系的性质定理

①线面垂直性质定理：

如果两条直线同垂直于一个平面，那么这两条直线平行。

②面面垂直的性质定理：

如果两个平面互相垂直，那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。

第三章直线与方程

3.1直线的倾斜角与斜率

（1）直线的倾斜角

x轴正向与直线向上方向之间所成的角叫直线的倾斜角。

特别地，当直线与x轴平行或重合时,我们规定它的倾斜角为0度。

因此，倾斜角的取值范围是0°

≤α＜180°

（2）直线的斜率

①定义：

倾斜角不是90°

的直线，它的倾斜角的正切叫做这条直线的斜率。

直线的斜率常用k表示。

即。

斜率反映直线与轴的倾斜程度。

当时，；

当时，；

当时，不存在。

②过两点的直线的斜率公式：

注意：

（1）当时，公式右边无意义，直线的斜率不存在，倾斜角为90°

；

（2）k与P1、P2的顺序无关；

（3）以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得；

（4）求直线的倾斜角可由直线上两点的坐标先求斜率得到。

3.2直线的方程

①点斜式：

直线斜率k，且过点

当直线的斜率为0°

时，k=0，直线的方程是y=y1。

当直线的斜率为90°

时，直线的斜率不存在，它的方程不能用点斜式表示．但因l上每一点的横坐标都等于x1，所以它的方程是x=x1。

②斜截式：

，直线斜率为k，直线在y轴上的截距为b

③两点式：

（）直线两点，

④截矩式：

其中直线与轴交于点,与轴交于点,即与轴、轴的截距分别为。

⑤一般式：

（A，B不全为0）

各式的适用范围特殊的方程如：

平行于x轴的直线：

（b为常数）；

平行于y轴的直线：

（a为常数）；

（5）直线系方程：

即具有某一共同性质的直线

（一）平行直线系

平行于已知直线（是不全为0的常数）的直线系：

（C为常数）

（二）过定点的直线系

（ⅰ）斜率为k的直线系：

，直线过定点；

（ⅱ）过两条直线，的交点的直线系方程为

（为参数），其中直线不在直线系中。

（6）两直线平行与垂直

当，时，

利用斜率判断直线的平行与垂直时，要注意斜率的存在与否。

3.3直线的交点坐标与距离公式

1、两条直线的交点

相交

交点坐标即方程组的一组解。

方程组无解；

方程组有无数解与重合

2、两点间距离公式：

设是平面直角坐标系中的两个点，

则

3、点到直线距离公式：

一点到直线的距离

4、两平行直线距离公式

在任一直线上任取一点，再转化为点到直线的距离进行求解。

第四章圆与方程

4.1圆的方程

1、圆的定义：

平面内到一定点的距离等于定长的点的集合叫圆，定点为圆心，定长为圆的半径。

2、圆的方程

（1）标准方程，圆心，半径为r；

（2）一般方程

当时，方程表示圆，此时圆心为，半径为

当时，表示一个点；

当时，方程不表示任何图形。

（3）求圆方程的方法：

一般都采用待定系数法：

先设后求。

确定一个圆需要三个独立条件，若利用圆的标准方程，

需求出a，b，r；

若利用一般方程，需要求出D，E，F；

另外要注意多利用圆的几何性质：

如弦的中垂线必经过原点，以此来确定圆心的位置。

4.2直线、圆的位置关系

1、直线与圆的位置关系有相离，相切，相交三种情况，基本上由下列两种方法判断：

（1）设直线，圆，圆心到l的距离为，则有；

（2）设直线，圆，先将方程联立消元，得到一个一元二次方程之后，令其中的判别式为，则有

注：

如果圆心的位置在原点，可使用公式去解直线与圆相切的问题，其中表示切点坐标，r表示半径。

（3）过圆上一点的切线方程：

①圆x2+y2=r2，圆上一点为（x0，y0），则过此点的切线方程为

②圆（x-a）2+（y-b）2=r2，圆上一点为（x0，y0），则过此点的切线方程为（x0-a）（x-a）+（y0-b）（y-b）=r2

2、圆与圆的位置关系：

通过两圆半径的和（差），与圆心距（d）之间的大小比较来确定。

设圆，

两圆的位置关系常通过两圆半径的和（差），与圆心距（d）之间的大小比较来确定。

当时两圆外离，此时有公切线四条；

当时两圆外切，连心线过切点，有外公切线两条，内公切线一条；

当时两圆相交，连心线垂直平分公共弦，有两条外公切线；

当时，两圆内切，连心线经过切点，只有一条公切线；

当时，两圆内含；

当时，为同心圆。

4.3空间直角坐标系

（1）定义：

如图，是单位正方体.以A为原点，

分别以OD,O,OB的方向为正方向，建立三条数轴。

这时建立了一个空间直角坐标系Oxyz.

1）O叫做坐标原点

2）x轴，y轴，z轴叫做坐标轴.

3）过每两个坐标轴的平面叫做坐标面。

（2）右手表示法：

令右手大拇指、食指和中指相互垂直时，可能形成的位置。

大拇指指向为x轴正方向，食指指向为y轴正向，中指指向则为z轴正向，这样也可以决定三轴间的相位置。

（3）任意点坐标表示：

空间一点M的坐标可以用有序实数组来表示，有序实数组叫做点M在此空间直角坐标系中的坐标，记作（x叫做点M的横坐