最新高中全国卷一北师大版高中数学必修一专题复习Word格式.doc

最新高中全国卷一北师大版高中数学必修一专题复习Word格式.doc

《最新高中全国卷一北师大版高中数学必修一专题复习Word格式.doc》由会员分享，可在线阅读，更多相关《最新高中全国卷一北师大版高中数学必修一专题复习Word格式.doc（57页珍藏版）》请在冰豆网上搜索。

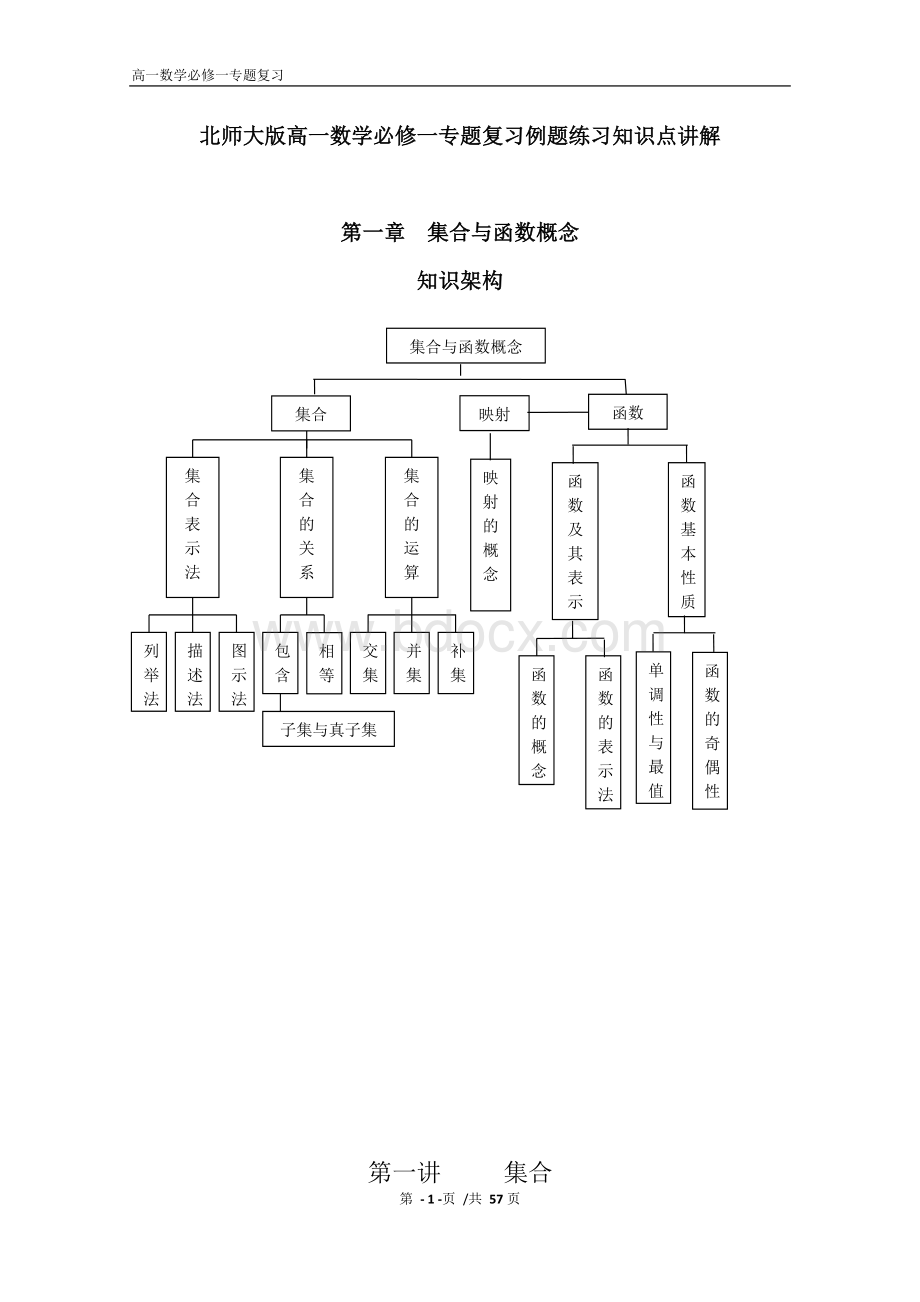
函数的概念

奇偶性

函数的表示法

映射

映射的概念

集合与函数概念

第一讲集合

★知识梳理

一：

集合的含义及其关系

1.集合中的元素具有的三个性质:

确定性、无序性和互异性;

2.集合的3种表示方法：

列举法、描述法、韦恩图；

3.集合中元素与集合的关系：

文字语言

符号语言

属于

不属于

4.常见集合的符号表示

数集

自然数集

正整数集

整数集

有理数集

实数集

复数集

符号

或

二：

集合间的基本关系

表示

关系

相等

集合A与集合B中的所有元素都相同

且

子集

A中任意一元素均为B中的元素

真子集

A中任意一元素均为B中的元素，且B中至少有一元素不是A的元素

空集

空集是任何集合的子集，是任何非空集合的真子集

，（）

三：

集合的基本运算

①两个集合的交集:

=;

②两个集合的并集:

=;

③设全集是U,集合,则

方法:

常用数轴或韦恩图进行集合的交、并、补三种运算.

★重、难点突破

重点：

集合元素的特征、集合的三种表示方法、集合的交、并、补三种运算。

难点：

正确把握集合元素的特征、进行集合的不同表示方法之间的相互转化，准确进行集合的交、并、补三种运算。

重难点：

1.集合的概念

掌握集合的概念的关键是把握集合元素的三大特性，要特别注意集合中元素的互异性，

在解题过程中最易被忽视，因此要对结果进行检验；

2．集合的表示法

（1）列举法要注意元素的三个特性；

（2）描述法要紧紧抓住代表元素以及它所具有的性质，如、、等的差别，如果对集合中代表元素认识不清，将导致求解错误：

问题：

已知集合（）

A.；

B.；

C.；

D.

[错解]误以为集合表示椭圆，集合表示直线，由于这直线过椭圆的两个顶点，于是错选B

[正解]C；

显然，，故

（3）Venn图是直观展示集合的很好方法，在解决集合间元素的有关问题和集合的运算时常用Venn图。

3．集合间的关系的几个重要结论

（1）空集是任何集合的子集，即

（2）任何集合都是它本身的子集，即

（3）子集、真子集都有传递性，即若，，则

4．集合的运算性质

（1）交集：

①；

②；

③；

④，⑤；

（2）并集：

（3）交、并、补集的关系

★热点考点题型探析

考点一：

集合的定义及其关系

题型1：

集合元素的基本特征

[例1]（2008年江西理）定义集合运算：

．设

，则集合的所有元素之和为（）

A．0；

B．2；

C．3；

D．6

[解题思路]根据的定义，让在中逐一取值，让在中逐一取值，在值就是的元素

[解析]：

正确解答本题,必需清楚集合中的元素，显然，根据题中定义的集合运算知=，故应选择D

【名师指引】这类将新定义的运算引入集合的问题因为背景公平，所以成为高考的一个热点，这时要充分理解所定义的运算即可，但要特别注意集合元素的互异性。

题型2：

集合间的基本关系

[例2]．数集与之的关系是（）

A．；

B．；

C．；

D．

[解题思路]可有两种思路：

一是将和的元素列举出来，然后进行判断；

也可依选择支之间的关系进行判断。

[解析]从题意看，数集与之间必然有关系，如果A成立，则D就成立，这不可能；

同样，B也不能成立；

而如果D成立，则A、B中必有一个成立，这也不可能，所以只能是C

【名师指引】新定义问题是高考的一个热点，解决这类问题的办法就是严格根据题中的定义，逐个进行检验，不方便进行检验的，就设法举反例。

[新题导练]

1．第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行，若集合A={参加北京奥运会比赛的运动员}，集合B={参加北京奥运会比赛的男运动员}，集合C={参加北京奥运会比赛的女运动员}，则下列关系正确的是（）

A．B.C.D.

[解析]D；

因为全集为，而=全集=

2．（2006•山东改编）定义集合运算:

设集合,,则集合的所有元素之和为

[解析]18，根据的定义，得到，故的所有元素之和为18

3．（2007·

湖北改编）设和是两个集合，定义集合，如果，,那么等于

[解析]；

因为，，所以

4．研究集合，，之间的关系

[解析]与，与都无包含关系，而；

因为表示

的定义域，故；

表示函数的值域，；

表示曲线上的点集，可见，，而与，与都无包含关系

考点二：

[例3]设集合，

（1）若，求实数的值；

（2）若，求实数的取值范围若，

[解题思路]对于含参数的集合的运算，首先解出不含参数的集合，然后根据已知条件求参数。

[解析]因为，

（1）由知，，从而得，即

，解得或

当时，，满足条件；

当时，，满足条件

所以或

（2）对于集合，由

因为，所以

①当，即时，，满足条件；

②当，即时，，满足条件；

③当，即时，才能满足条件，

由根与系数的关系得，矛盾

故实数的取值范围是

【名师指引】对于比较抽象的集合，在探究它们的关系时，要先对它们进行化简。

同时，要注意集合的子集要考虑空与不空,不要忘了集合本身和空集这两种特殊情况.

6．若集合，，则是（）

C.；

D.有限集

[解析]A；

由题意知，集合表示函数的值域，故

集合；

表示函数的值域，

，故

7．已知集合，，那么集合为（）A.；

B.；

D.

[解析]D；

表示直线与直线的交点组成的集合，A、B、C均不合题意。

8．集合,,且,求实数的值.

先化简B得,.由于,故或.

因此或,解得或.

容易漏掉的一种情况是:

的情形,此时.

故所求实数的值为.

备选例题1：

已知，，则中的元素个数是（）

D.无穷多个

[解析]选A;

集合表示函数的值域,是数集,并且,而集合表示满足

的有序实数对的集合,即表示圆上的点,是点集。

所以，集合与集合中的元素均不相同，因而，故其中元素的个数为0

[误区分析]在解答过程中易出现直线与圆有两个交点误选C；

或者误认为中，而中，从而有无穷多个解而选D。

注意，明确集合中元素的属性（是点集还是数集）是准确进行有关集合运算的前提和关键。

备选例题2：

已知集合和集合各有12个元素，含有4个元素，试求同时满足下面两个条件的集合的个数：

（Ⅰ），且中含有3个元素；

（Ⅱ）（表示空集）

[解法一]因为、各有12个元素，含有4个元素，

因此，的元素个数是

故满足条件（Ⅰ）的集合的个数是

上面集合中，还满足的集合的个数是

因此，所求集合的个数是

[解法二]由题目条件可知，属于而不属于的元素个数是

因此，在中只含有中1个元素的所要求的集合的个数为

含有中2个元素的所要求的集合的个数为

含有中3个元素的所要求的集合的个数为

所以，所求集合的个数是

★抢分频道

U

B

A

基础巩固训练：

1．（09年吴川市川西中学09届第四次月考）设全集

则右图中阴

影部分表示的集合为（）

C．；

[解析]C；

图中阴影部分表示的集合是，而，故

2.（韶关09届高三摸底考）已知则=

3.（苏州09届高三调研考）集合的所有子集个数为

[解析]8；

集合的所有子集个数为

4.（09年无锡市高三第一次月考）集合中的代表元素设为，集合中的代表元素设为，若且，则与的关系是

[解析]或；

由子集和交集的定义即可得到结论

5．（2008年天津）设集合，则的取值范围是（）

B．

C．或；

D．或

[解析]A；

，，

所以，从而得

综合提高训练：

6．,

则下列关系中立的是（）

A．;

B．;

C．;

当时，有，即

；

当时，也恒成立，故

，所以

7.设，，，记

，，则＝（）

A.;

B.;

C.;

D.

依题意得，，所以，

，故应选A

8．（09届惠州第一次调研考）设A、B是非空集合，定义

，已知A=，B=，

则A×

B等于（）

，∴A=[0，2]，，∴B=（1，＋∞），

∴A∪B=[0,＋∞），A∩B=（1，2]，则A×

B＝

第2讲函数与映射的概念

1．函数的概念

（1）函数的定义：

设是两个非空的数集，如果按照某种对应法则，对于集合中的每一个数，在集合中都有唯一确定的数和它对应，那么这样的对应叫做从到的一个函数，通常记为

（2）函数的定义域、值域

在函数中，叫做自变量，的取值范围叫做的定义域；

与的值相对应的值叫做函数值，函数值的集合称为函数的值域。

（2）函数的三要素：

定义域、值域和对应法则

2．映射的概念

设是两个集合，如果按照某种对应法则，对于集合中的任意元素，在集合中都有唯一确定的元素与之对应，那么这样的单值对应叫做从到的映射，通常记为

掌握映射的概念、函数的概念，会求函数的定义域、值域

求函数的值域和求抽象函数的定义域

1．关于抽象函数的定义域

求抽象函数的定义域，如果没有弄清所给函数之间的关系，求解容易出错误

问题1：

已知函数的定义域为，求的定义域

[误解]因为函数的定义域为，所以，从而

故的定义域是

[正解]因为的定义域为，所以在函数中，，

从而，故的定义域是

即本题的实质是求中的范围

问题2：

已知的定义域是，求函数的定义域

[误解]因为函数的定义域是，所以得到，从而

，所以函数的定义域是

[正解]因为函数的定义域是，则，从而

所以函数的定义域是

即本题的实质是由求的范围

即与中含义不同

2．求值域的几种常用方法

（1）配方法：

对于（可化为）“二次函数型”的函数常用配方法，如求函数，可变为解决

（2）基本函数法：

一些由基本函数复合而成的函数可以利用基本函数的值域来求，如函数就是利用函数和的值域来求。

（3）判别式法：

通过对二次方程的实根的判别求值域。

如求函数的值域

由得，若，则得，所以是函数值域中的一个值；

若，则由得，故所求值域是

（4）分离常数法：

常用来求“分式型”函数的值域。

如求函数的值域，因为

，而，所以，故

（5）利用基本不等式求值域：

当时，；

当时，，若，则

若，则，从而得所求值域是

（6）利用函数的单调性求求值域：

因，故函数在上递减、在上递增、在上递减、在上递增，从而可得所求值域为

（7）图象法：

如果函数的图象比较容易作出，则可根据图象直观地得出函数的值域（求某些分段函数的值域常用此法）。

判断两函数是否为同一个函数

[例1]试判断以下各组函数是否表示同一函数