数学建模题目Word文档格式.doc

数学建模题目Word文档格式.doc

《数学建模题目Word文档格式.doc》由会员分享，可在线阅读，更多相关《数学建模题目Word文档格式.doc（29页珍藏版）》请在冰豆网上搜索。

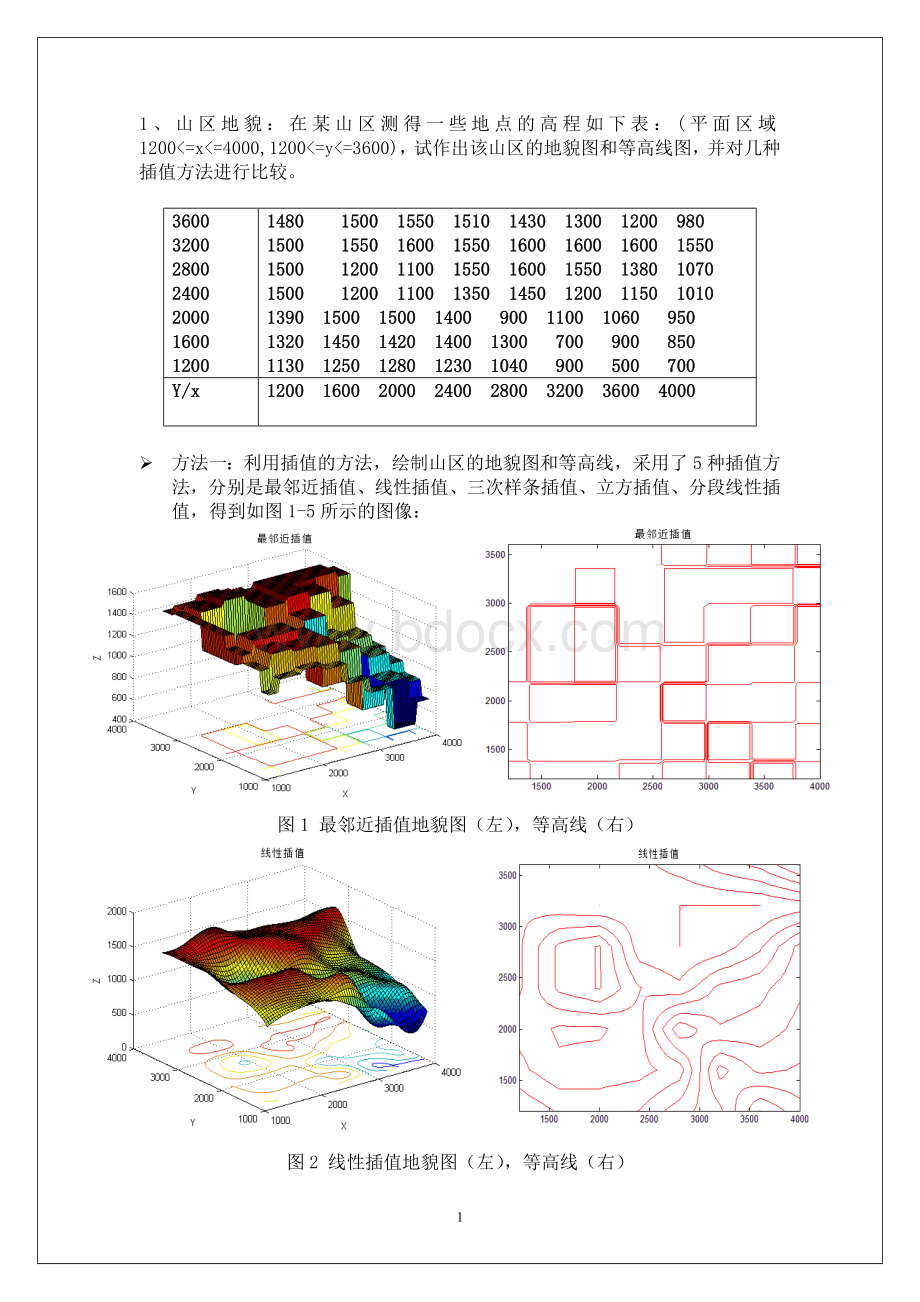
图1最邻近插值地貌图（左），等高线（右）

图2线性插值地貌图（左），等高线（右）

图3三次样条插值地貌图（左），等高线（右）

图4立方插值地貌图（左），等高线（右）

图5分段线性插值地貌图（左），等高线（右）

比较由以上五种插值方法得到的地貌图和等高线图，可以看出，由于两个高度之间直线为最短距离，因此利用最邻近插值得到的地貌图和等高线为直线，描述的山地地貌为陡崖，对于一般山区的地貌是不符合的；

分段线性插值得到的图像随着分段数目的增多，而更加平缓，棱角更加不明显；

利用线性插值、三次样条插值和立方插值所得到的图像，较为平滑，更加适合描述该区山地的地貌。

图像绘制程序：

x=1200:

400:

4000;

y=1200:

3600;

z=[11301250128012301040900500700;

13201450142014001300700900850;

139015001500140090011001060950;

1500 1200110013501450120011501010;

1500 1200110015501600155013801070;

1500 1550160015501600160016001550;

1480 150015501510143013001200980];

figure

（1）;

meshz（x,y,z）

xlabel（'

X'

）,ylabel（'

Y'

）,zlabel（'

Z'

）

title（'

网格面'

xi=1200:

40:

yi=1200:

figure

（2）

z1i=interp2（x,y,z,xi,yi'

'

nearest'

）;

%最邻近插值

%subplot（1,2,1）,

surfc（xi,yi,z1i）

最邻近插值'

%subplot（1,2,2）,contour（xi,yi,z1i,10,'

r'

figure（3）

z2i=interp2（x,y,z,xi,yi'

surfc（xi,yi,z2i）

）%分段线性插值

分段线性插值'

%subplot（1,2,2）,contour（xi,yi,z2i,10,'

figure（4）

z3i=interp2（x,y,z,xi,yi'

cubic'

surfc（xi,yi,z3i）

）%立方插值

立方插值'

figure（5）

z4i=interp2（x,y,z,xi,yi'

spline'

surfc（xi,yi,z4i）

）%三次样条插值%

三次样条插值'

figure（6）

z5i=interp2（x,y,z,xi,yi'

linear'

）%线性插值

线性插值'

figure（7）

subplot（3,2,1）,contour（xi,yi,z1i,10,'

subplot（3,2,2）,contour（xi,yi,z2i,10,'

subplot（3,2,3）,contour（xi,yi,z3i,10,'

subplot（3,2,4）,contour（xi,yi,z4i,10,'

subplot（3,2,5）,contour（xi,yi,z5i,10,'

%compare

figure（8）

contour（xi,yi,z1i,10,'

figure（9）

contour（xi,yi,z2i,10,'

）

figure（10）

contour（xi,yi,z3i,10,'

figure（11）

contour（xi,yi,z4i,10,'

figure（12）

contour（xi,yi,z5i,10,'

方法二：

针对绘制等高线和地貌图的问题，使用Matlab中的contourf命令绘制等高线，surf命令绘制带阴影的三维曲面图，得到地貌图，如图6所示的地貌图和平面等高线：

图6山区地貌图（左），等高线图（右）

（1）等高线绘制程序：

clc;

clf;

clear;

holdon

c=contourf（x,y,z,10）;

clabel（c）

（2）地貌图绘制程序：

figure

surf（x,y,z）,view（50,30）,holdon

2、假定某地某天的气温变化记录数据见下表，误差不超过0.5℃，试找出其这一天的气温变化规律。

时刻/h

1

2

3

4

5

6

7

8

9

10

11

12

13

温度/℃

15

14

16

18

20

22

23

25

28

31

17

19

21

24

32

29

27

07

对的温度进行分析，采用多项式拟合的数学方法，建立温度和时刻的模型，利用Matlab编写程序求得多项式方程为：

拟合所得图像如图7所示：

图7温度-时间拟合曲线

由图像可以看出，在内，温度变化较平缓，在℃左右；

在温度处于上升阶段，在出现最高温度℃；

从处于下降阶段，其中在时出现了低温7℃。

程序：

x=0:

1:

24;

y=[15 14 14 14 14 15 16 18 20 22 23 25 28 313231 29 27 25 24 22 20 18 07 16];

plot（x,y,'

r*'

holdon

a=polyfit（x,y,5）;

z=a

（1）*x.^5+a

（2）*x.^4+a（3）*x.^3+a（4）*x.^2+a（5）*x+a（6）;

plot（x,z）

grid;

holdoff

3、财政收入预测问题：

财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。

下表列出了1952-1981年的原始数据，试构造回归预测模型，并利用1982-1990的数据验证模型。

年份

国民收入（亿元）

工业总产值（亿元）

农业总产值（亿元）

总人口（万人）

就业人口（万人）

固定资产投资（亿元）

财政收入（亿元）

1952

598

349

461

57482

20729

44

184

1953

586

455

475

58796

21364

89

216

1954

707

520

491

60266

21832

97

248

1955

737

558

529

61465

22328

98

254

1956

825

715

556

62828

23018

150

268

1957

837

798

575

64653

23711

139

286

1958

1028

1235

65994

26600

256

357

1959

1114

1681

509

67207

26173

338

444

1960

1079

1870

66207

25880

380

50