编码与译码离散数学文档格式.docx

编码与译码离散数学文档格式.docx

《编码与译码离散数学文档格式.docx》由会员分享，可在线阅读，更多相关《编码与译码离散数学文档格式.docx（10页珍藏版）》请在冰豆网上搜索。

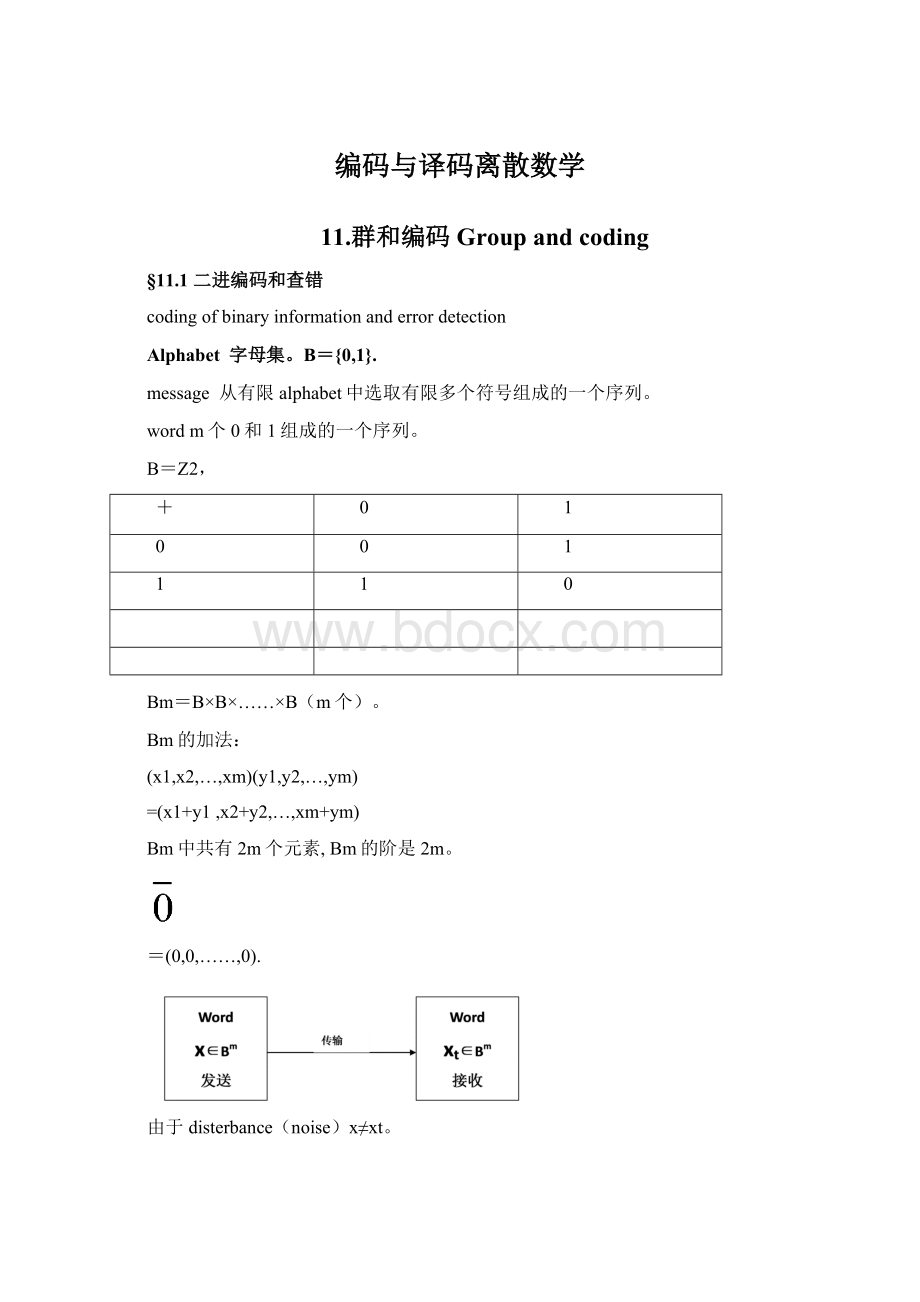
＝（0,0,……,0）.

由于disterbance（noise）x≠xt。

用编码方法查错、纠错。

取n>

m，一一对应 

e：

Bm→Bn，

称e是（m,n）编码函数。

b∈Bm，e（b）∈Bn叫做b的码词Codeword

e（b）比b多几位0，1用来查错和纠错。

将要发出的wordb编码得到x=e（b）,发送后接收到xt，如果没有干扰，x＝xt，b＝e-1（xt）.

如果有干扰，x和xt有≤k位出错，即有1位到k位错误。

x的权（weight）：

x含有1的个数，记做|x|.

奇偶校验码paritycheckcode：

如果b＝b1b2…bm，

令e（b）＝b1b2…bmbm+1,

bm+1=0,if|b|是偶数，

bm+1=1,if|b|是奇数。

bm+1=0,当且仅当b含有偶数个1。

m＝3

e（000）=0000

e（001）=0011

e（010）=0101

e（011）=0110

e（100）=1001

e（101）=1010

e（110）=1100

e（111）=1111

对任意b，e（b）的权总是偶数。

设b=111，x＝e（b）=1111.

如果接收到有一位错xt＝1101，

xt的权是奇数，发现有错。

xt的权是偶数，无法判断有错。

例3．（m，3m）编码函数：

e：

Bm→B3m， 

b＝b1b2…bm，

e（b）＝b1b2…bmb1b2…bmb1b2…bm.

e（000）=000000000

e（001）=001001001

e（010）=010010010

e（011）=011011011

e（100）=100100100

e（101）=101101101

e（110）=110110110

e（111）=111111111

可以发现一位或两位错误。

海明距离δ（x,y）：

Hammingdistance

设x，y∈Bm，δ（x,y）=|xy|

δ（x,y）等于x，y中对应不相等的位置的个数。

例4．求海明距离

x=110110,y=000101

x=001100,y=010110

解.（a）δ（x,y）=4.

（b）δ（x,y）=3.

定理1.设x,y,z∈Bm，则

δ（x,y）=δ（y,x）.

δ（x,y）≥0.

δ（x,y）=0iffx=y.

δ（x,y）≤δ（x,z）＋δ（z,y）

证明.

（d）|ab|≤|a|+|b|.

δ（x,y）=|x

y|=|xzzy|

≤|xz|+|zy|=δ（x,y）+δ（x,y）

一个编码函数e：

Bm→Bn的最小距离minimundistance：

min{δ（e（x）,e（y））|x,y∈Bm}.

例5．e（00）=00000

e（01）=01110

e（10）=00111

e（11）=11111

min{δ（e（x）,e（y））}=2.

定理2.一个（m，n）编码e：

Bm→Bn能查出至多k位错误当且仅当最小海明距离≥k＋1。

证明.设最小海明距离≥k＋1。

发出x＝e（b）,收到xt，x≠xt，

δ（x,xt）≤k，则xt不是一个编码，查出错误。

反之.设最小海明距离＝r≤k。

δ（x,xt）＝r，xt可能是另一个编码无法判断错误。

例6.

能查几位错？

群编码Groupcodes

Bm→Bn叫做群编码，如果Ran（e）=e（Bm）={e（b）|b∈Bm}

是Bn的一个子群。

例7.

（1） 

e（000）=000000000

是群编码。

（2）

e（000）=000000

e（001）=001100

e（010）=010011

e（011）=011111

e（100）=100101

e（101）=101001

e（110）=110110

e（111）=111010

也是群编码。

定理3.设e：

Bm→Bn是一个群编码，则e的最小海明距离等于非零元的最小权。

证明.设δ是e的最小海明距离，η是非零元的最小权。

δ＝δ（x,y）,η＝|z|.δ（x,y）=|xy|≥η。

η＝|z|＝|z0|＝δ（z,0）≥δ。

因此δ＝η。

例8.例7

（1）δ＝3.

（2）δ＝2.

例9.布尔矩阵的加法和乘法：

定理4.布尔矩阵的乘法对加法满足分配律：

设D，E是m×

p布尔矩阵，F是p×

n布尔矩阵，则（DE）*F=（D*F）（E*F）.

定理5.设非负整数m<

n,r=m-n,H是n×

r布尔矩阵。

fH：

Bn→Br, 

fH（x）=x*H.则fH是群Bn到Br内的同态映射。

证明.任意x，y∈Bn,

fH（xy）＝（xy）*H=（x*H）（y*H）

=fH（x）fH（y）.

推论1.N={x∈Bn|x*H=

}是Bn的正规子群。

令m<

r布尔矩阵

r＝n－m行

令eH：

Bm→Bn

eH（b1b2…bm）＝b1b2…bmx1x2…xr，

x1＝b1h11+b2h21+…+bmhm1，

x2＝b1h12+b2h22+…+bmhm2，

xr＝b1h1r+b2h2r+…+bmhmr，

定理6.令x＝y1y2…ymx1…xr，则x*H=

当且仅当存在b∈Bm,x=eH（b）.

证明.设x*H=

y1h11+y2h21+…+ymhm1+x1=0

y1h12+y2h22+…+ymhm2+x2=0

y1h1r+y2h2r+…+ymhmr+xr=0

两边同加xi，

y1h11+y2h21+…+ymhm1+x1+x1=0+x1

y1h11+y2h21+…+ymhm1=x1

y1h12+y2h22+…+ymhm2=x2

y1h1r+y2h2r+…+ymhmr=xr

x=eH（y）.

设存在b∈Bm,x=eH（b）.

b1h11+b2h21+…+bmhm1＋x1＝0

b1h12+b2h22+…+bmhm2＋x2＝0，

b1h1r+b2h2r+…+bmhmr＋xr＝0

即x*H=

.

推论2.eH（Bm）={eH（b）|b∈Bm}是Bn的子群。

eH是群编码。

证明.eH（Bm）=ker（fH）.

例11．m＝2，n＝5，给出群编码

eH：

B2→B5,

解.eH（00）=00x1x2x3,

x1=x2=x3=0,eH（00）=00000.

eH（01）=01x1x2x3,

x1=0, 

x2=1, 

x1=1,

eH（01）=01011

eH（10）=10110,

eH（11）=11101.

δ＝3.可查2位。

11.2解码和纠错Decodinganderrorcorrection

例1

设奇偶编码e：

Bm→Bm+1,

令d：

Bm+1→Bm是解码函数，

任意y＝y1y2…ymym+1,

d（y）=y1y2…ym.

d（e（b）=b.

d?

e=1Bm.

d可以解码，不能纠错。

设编码e：

Bm→Bn,

Bn→Bm是e的解码函数，

如果传送x＝e（b）,接收xt，至多k位错，d（xt）=b,就称d为e的k位纠错解码，也称（e，d）k位纠错。

例2

（m,3m）编码，定义解码函数d：

B3m→Bm，对

y＝y1y2…ymym+1…y2my2m＋1…y3m,

d（y）=z1z2…zm, 

zi=1if{zi,zi+m,zi+2m}含有至少2个1.

zi=0if{zi,zi+m,zi+2m}含有少于2个1.

d是1位纠错解码

最大似然解码函数maximumlikelihooddecodingfunction

列出Bm中所有2m个元素：

x

（1）,x

（2）,……，

如果接收的是xt，找出第一个x（s）,使

δ（x（s）,xt）=min1≤i≤2m{δ（x（i）,xt）}.

取d（xt）=e-1（x（s））=b.

称d为e的最大似然解码函数。

d与列出Bm中2m个元素的次序有关。

定理1.

设e：

Bm→Bn是编码，d：

Bn→Bm是e的最大似然解码函数。

则（e，d）能纠至多k位错当且仅当e的最小距离至少2k＋1。

设e的最小距离至少2k＋1。

令b∈Bm，x＝e（b）∈Bn，如果发送x，接收xt，至多k位错。

δ（x,xt）≤k.

设z是一个编码，z≠x，

2k＋1≤δ（x,z）≤δ（x,xt）+δ（xt,z）≤k＋δ（xt,z）.

δ（xt,z）≥k＋1.

于是z不可能是xt的源码，x是唯一的与xt最接近的编码，d（xt）=b.

因此（e，d）k位纠错。

反之,假设最小海明距离r≤2k。

令x＝e（b）,x’＝e（b’）,δ（b,b’）=r.