运筹学实验报告向市场运送木材问题教材文档格式.docx

运筹学实验报告向市场运送木材问题教材文档格式.docx

《运筹学实验报告向市场运送木材问题教材文档格式.docx》由会员分享，可在线阅读，更多相关《运筹学实验报告向市场运送木材问题教材文档格式.docx（16页珍藏版）》请在冰豆网上搜索。

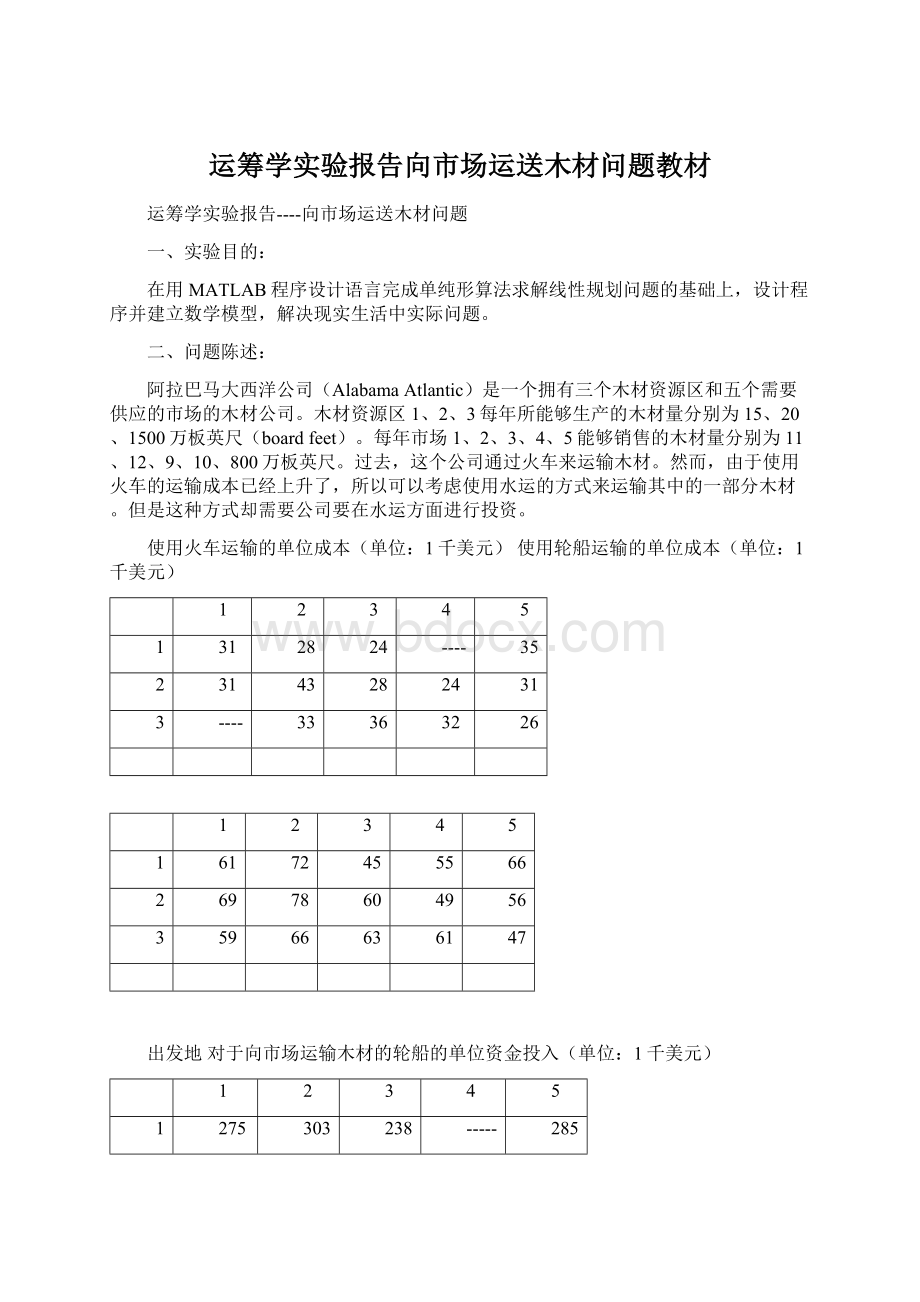
31

28

24

----

35

43

33

36

32

26

61

72

45

55

66

69

78

60

49

56

59

63

47

出发地对于向市场运输木材的轮船的单位资金投入（单位：

275

303

238

-----

285

293

318

270

250

265

283

268

240

考虑到轮船的预计使用期限（大约30年）和货币的时间价值，年金成本大约是当年投入资金的十分之一。

公司的目标是要制订出一个全面运输计划，使总年金成本最小（包括运输成本）。

现在，如果你是公司管理科学小组的负责人。

那么所需要做的工作是根据下面所给出的三种选择分别制订出这种能够使得年金成本最小的运输计划。

选择l：

继续使用火车来运输木材，并仅使用这一种方式。

选择2：

仅使用轮船运输木材（只能使用火车的地方除外）。

选择3：

根据在每一条特定的路线上哪种方式的运输成本比较低来选择使用火车还是轮船来运输木材。

根据上述每一种情况，列出各自的数学模型，并用MATLAB求解，最终比较哪一种方案比较好。

三、问题分析

情况一：

只用火车运输木材，根据如下列表

可列方程如下：

（z为一年基本运费，xij为i号生产地向j号销售地运输量）

minz=61x1+72x2+45x3+55x4+66x5+69x6+78x7+60x8+49x9+56x10+59x11+66x12+63x13+61x14+47x15

s.t.x1+x2+x3+x4+x5<

15

x6+x7+x8+x9+x10<

20

x11+x12+x13+x14+x15<

1500

x1+x6+x11=11

x2+x7+x12=12

x3+x8+x13=9

x4+x9+x14=10

x5+x10+x15=800

xj≥0,j=1,…,15

根据上述列出的方程关系，相应的A，b，c的值到已有的程序中：

>

linp3

A=[111110000000000100;

000001111100000010;

000000000011111001;

100001000010000000;

010000100001000000;

001000010000100000;

000100001000010000;

000010000100001000]

b=[15;

20;

1500;

11;

12;

9;

10;

800]

c=[617245556669786049565966636147000]

中间运行过程省略。

已找到最优解!

最优可行解为:

x=

0

9

10

11

12

800

6

677

最优值为:

minf=

39936

最优解对应的单纯形表为:

optmatrx=

Columns1through7

-2-60-6-19-10-12

1000010

0001000

-1-100-1-1-1

0100001

1101100

000-1011

0010000

0000100

Columns8through14

-150-900-18-12

00-10011

-10000-10

101000-1

Columns15through19

000039936

000011

000010

0001677

000012

01006

001010

00009

1000800

情况二：

只用轮船运输木材，根据列表可列方程如下：

minz=31x1+28x2+24x3+55x4+35x5+31x6+43x7+28x8+24x9+31x10+59x11+33x12+36x13+32x14+26x15

根据上述列出的方程关系，在程序中进行测试：

运行结果如下：

c=[312824553531432824315933363226000]

中间运行结果省略。

1

5

7

693

21968

000-31-140-15

0100101

100100-1

0000000

0000-100

-40-10-230-7-3

001-10-1-1

-10-11001

00-11111

0-5-5021968

01105

00-101

0111693

0-1-107

题目可知，轮船的预计使用期限为30年，年金成本是当年投入资金的十分之一。

为使总年金成本最小，还需加上对轮船的资金投入，对轮船的单位资金投入如下表：

因总年金成本含有运输成本以及年金成本，所以有：

W=min*（1.1^0+1.1^1+1.1^2+……+1.1^29）+minw*1.1^29

min为上述程序算出的最小运费为21968千美元，minw为上述程序算出最优解时要用到的线路的最初投入钱数的总和。

W为最后30年所需总年金成本。

所需线路如下：

需要

根据计算得到最后结果为w=3643460千美元（30年）

情况三：

假设每一条线路所需运输货物一吨，比较该路的水路和火车30年所需总费用，选取最小方式为该路的运输方式。

当没有水路时，则只能选取火车方式，可列式子如下：

Tij=P1ij*（1.1^0+1.1^1+1.1^2+……+1.1^29）

Qij=P2ij*（1.1^0+1.1^1+1.1^2+……+1.1^29）+PCij*1.1^29

Tij、Qij分别表示火车或轮船从i号生产地向j号销售地每年运输一吨，30年总共所需钱数。

P1ij、P2ij分别表示火车、轮船在该线路的单位运输费，PCij为该线路最初对轮船投入的钱数。

进行比较后的结果如下