浙江专版高考数学一轮复习第5章数列第1节数列的概念与简单表示法教师用书文档格式.docx

浙江专版高考数学一轮复习第5章数列第1节数列的概念与简单表示法教师用书文档格式.docx

《浙江专版高考数学一轮复习第5章数列第1节数列的概念与简单表示法教师用书文档格式.docx》由会员分享，可在线阅读，更多相关《浙江专版高考数学一轮复习第5章数列第1节数列的概念与简单表示法教师用书文档格式.docx（13页珍藏版）》请在冰豆网上搜索。

19,4分（文）

18,14分（理）

19,14分（文）

等比数列及前n项和

17

（1），7

分（文）

3,5分（理）

17,3分（文）

19,4（理）

18

（1），6分（理）

19,3分（文）

13,4分（理）

数列求和及综合应用

13,6分（理）

20,15分（理）

17

（2），8

17,15分（文）

19,14分（理）

18,14分（理）

14,4分（文）

19,7分（文）

[重点关注]

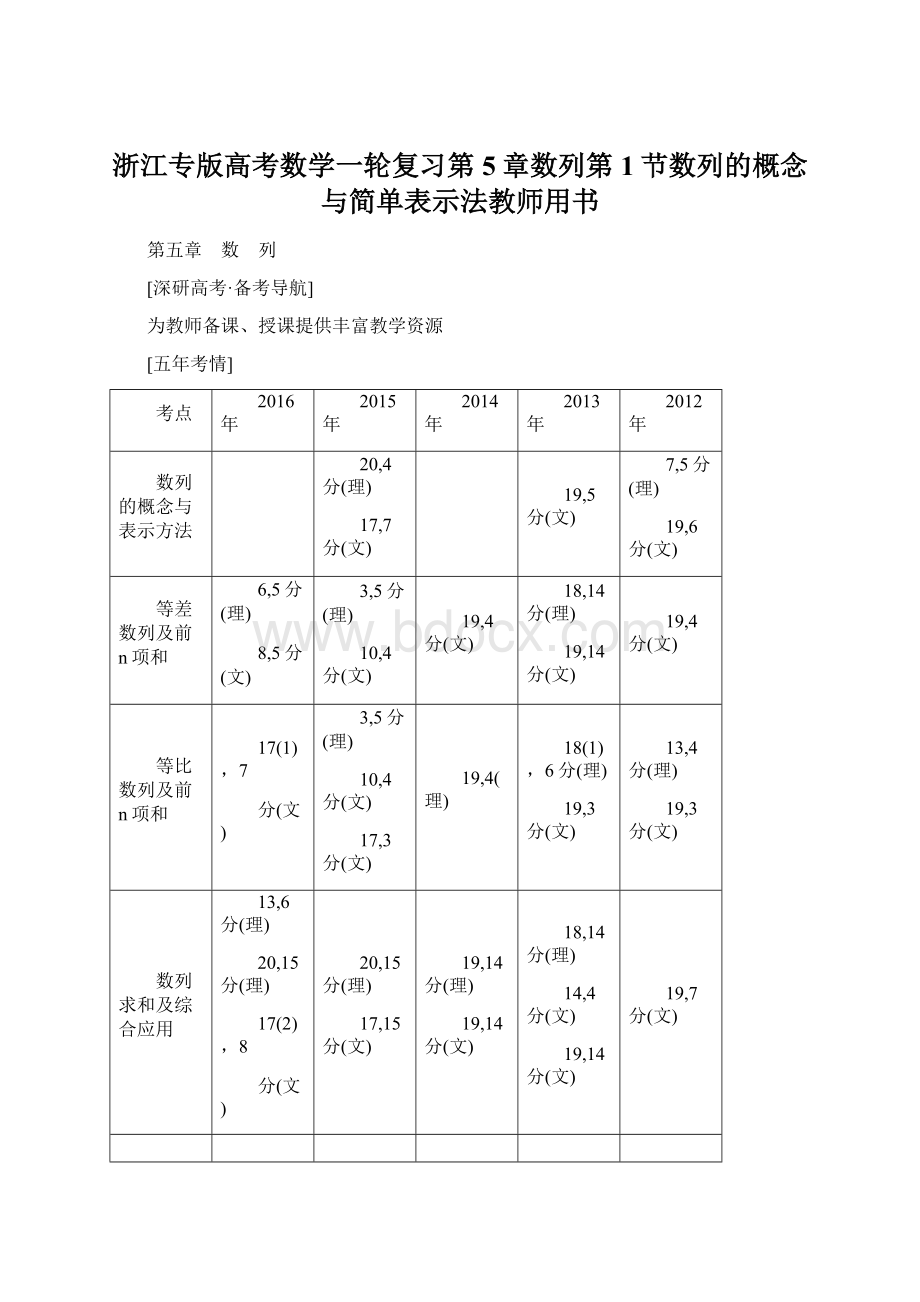
从近五年浙江卷高考试题来看，数列是高考命题的热点，主要考查等差数列，等比数列，an与Sn的关系，递推公式以及数列求和，数列与不等式的交汇也成为高考命题的重点．

第一节　数列的概念与简单表示法

1．数列的定义

按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项．

2．数列的分类

分类标准

类型

满足条件

项数

有穷数列

项数有限

无穷数列

项数无限

单调性

递增数列

an＋1>

an

其中

n∈N*

递减数列

an＋1<

常数列

an＋1＝an

摆动数列

从第2项起，有些项大于它的前一项，有些项小于它的前一项的数列

3.数列的表示法

数列有三种表示法，它们分别是列表法、图象法和解析法．

4．数列的通项公式

如果数列{an}的第n项与序号n之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式．

5．数列的递推公式

如果已知数列的第1项（或前几项），且从第二项（或某一项）开始的任一项an与它的前一项an－1（或前几项）间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式．

6．an与Sn的关系

若数列{an}的前n项和为Sn，通项公式为an，

则an＝

1．（思考辨析）判断下列结论的正误．（正确的打“√”，错误的打“×

”）

（1）所有数列的第n项都能使用公式表达．（　　）

（2）根据数列的前几项归纳出数列的通项公式可能不止一个．（　　）

（3）如果数列{an}的前n项和为Sn，则对∀n∈N*，都有an＋1＝Sn＋1－Sn.（　　）

（4）若已知数列{an}的递推公式为an＋1＝，且a2＝1，则可以写出数列{an}的任何一项．（　　）

[答案]　

（1）×

（2）√　（3）√　（4）√

2．设数列{an}的前n项和Sn＝n2，则a8的值为（　　）

A．15　　　　　　B．16

C．49D．64

A　[当n＝8时，a8＝S8－S7＝82－72＝15.]

个正三角形（如图511）．

图511

则第7个三角形数是（　　）

A．27　　　B．28　　　C．29　　　D．30

B　[由题图可知，第7个三角形数是1＋2＋3＋4＋5＋6＋7＝28.]

4．（教材改编）数列1，，，，，…的一个通项公式an是__________．

　[由已知得，数列可写成，，，…，故通项为.]

5．（2017·

保定调研）在数列{an}中，已知a1＝1，an＋1＝2an＋1，则其通项公式an＝2n－1　[法一：

由an＋1＝2an＋1，可求a2＝3，a3＝7，a4＝15，…，验证可知an＝2n－1.

法二：

由题意知an＋1＋1＝2（an＋1），∴数列{an＋1}是以2为首项，2为公比的等比数列，∴an＋1＝2n，∴an＝2n－1.]

由数列的前几项归纳数列的

通项公式

　写出下面各数列的一个通项公式：

（2），，，，，…；

（3）－1,7，－13,19，…；

[解]　

（1）各项减去1后为正偶数，所以an＝2n＋1.2分

所以an＝.6分

（3）数列中各项的符号可通过（－1）n表示，从第2项起，每一项的绝对值总比它的前一项的绝对值大6.

故通项公式为an＝（－1）n（6n－5）.10分

（4）将数列各项改写为，，，，…，分母都是3，而分子分别是10－1,102－1,103－1,104－1，…，

所以an＝（10n－1）.14分

[规律方法]　1.求数列通项时，要抓住以下几个特征：

（1）分式中分子、分母的特征；

（2）相邻项的变化特征；

（3）拆项后变化的部分和不变的部分的特征；

（4）各项符号特征等，并对此进行归纳、化归、联想．

2．若关系不明显时，应将部分项作适当的变形，统一成相同的形式，让规律凸现出来．对于正负符号变化，可用（－1）n或（－1）n＋1来调整，可代入验证归纳的正确性．

[变式训练1]　

（1）数列0，，，，…的一个通项公式为（　　）

A．an＝（n∈N*）

B．an＝（n∈N*）

C．an＝（n∈N*）

D．an＝（n∈N*）

（2）数列{an}的前4项是，1，，，则这个数列的一个通项公式是an＝__________.

（2）数列{an}的前4项可变形为，，，，故an＝.]

由an与Sn的关系求通项an

　已知下面数列{an}的前n项和Sn，求{an}的通项公式：

（1）Sn＝2n2－3n；

[解]　

（1）a1＝S1＝2－3＝－1，

当n≥2时，an＝Sn－Sn－1＝（2n2－3n）－[2（n－1）2－3（n－1）]＝4n－5，3分

由于a1也适合此等式，∴an＝4n－5.6分

（2）a1＝S1＝3＋b，

当n≥2时，an＝Sn－Sn－1＝（3n＋b）－（3n－1＋b）＝2·

3n－1.9分

当b＝－1时，a1适合此等式．

当b≠－1时，a1不适合此等式.12分

∴当b＝－1时，an＝2·

3n－1；

当b≠－1时，an＝14分

[规律方法]　由Sn求an的步骤

（1）先利用a1＝S1求出a1；

（2）用n－1替换Sn中的n得到一个新的关系，利用an＝Sn－Sn－1（n≥2）便可求出当n≥2时an的表达式；

（3）对n＝1时的结果进行检验，看是否符合n≥2时an的表达式，如果符合，则可以把数列的通项公式合写；

如果不符合，则应写成分段函数的形式．

易错警示：

利用an＝Sn－Sn－1求通项时，应注意n≥2这一前提条件，易忽视验证n＝1致误．

[变式训练2]　（2017·

绍兴质检

（二））已知数列{an}的前n项和为Sn，若Sn＝2an－4（n∈N*），则an＝（　　）

A．2n＋1　　　　　　　B．2n

C．2n－1D．2n－2

A　[由Sn＝2an－4可得Sn－1＝2an－1－4（n≥2），两式相减可得an＝2an－

2an－1（n≥2），即an＝2an－1（n≥2）．又a1＝2a1－4，a1＝4，所以数列{an}是以4为首项，2为公比的等比数列，则an＝4×

2n－1＝2n＋1，故选A.]

由递推公式求数列的通项公式

　根据下列条件，确定数列{an}的通项公式：

（1）a1＝2，an＋1＝an＋3n＋2；

（2）a1＝1，an＋1＝2nan；

（3）a1＝1，an＋1＝3an＋2.

[解]　

（1）∵an＋1－an＝3n＋2，

∴an－an－1＝3n－1（n≥2），

∴an＝（an－an－1）＋（an－1－an－2）＋…＋（a2－a1）＋a1＝（n≥2）．

当n＝1时，a1＝×

（3×

1＋1）＝2符合公式，

∴an＝n2＋.4分

（2）∵an＋1＝2nan，∴＝2n－1（n≥2），

∴an＝·

·

…·

a1

＝2n－1·

2n－2·

2·

1＝21＋2＋3＋…＋（n－1）＝.

又a1＝1适合上式，故an＝.9分

（3）∵an＋1＝3an＋2，∴an＋1＋1＝3（an＋1），

又a1＝1，∴a1＋1＝2，

故数列{an＋1}是首项为2，公比为3的等比数列，

∴an＋1＝2·

3n－1，因此an＝2·

3n－1－1.14分

[规律方法]　1.已知a1，且an－an－1＝f（n），可用“累加法”求an；

已知a1（a1≠0），且＝f（n），可用“累乘法”求an.

2．已知a1，且an＋1＝qan＋b，则an＋1＋k＝q（an＋k）（其中k可由待定系数法确定），可转化为{an＋k}为等比数列．

本题

（1），

（2）中常见的错误是忽视验证a1是否适合所求式，（3）中常见错误是忽视判定首项是否为零．

[变式训练3]　已知各项都为正数的数列{an}满足a1＝1，a－（2an＋1－1）an－2an＋1＝0.

（1）求a2，a3；

（2）求{an}的通项公式．

[解]　

（1）由题意可得a2＝，a3＝.4分

（2）由a－（2an＋1－1）an－2an＋1＝0得

2an＋1（an＋1）＝an（an＋1）.8分

因为{an}的各项都为正数，所以＝.12分

故{an}是首项为1，公比为的等比数列，因此an＝.14分

[思想与方法]

1．数列是一种特殊的函数，因此，在研究数列问题时，既要注意函数方法的普遍性，又要考虑数列方法的特殊性．

2．an＝

3．由递推关系求数列的通项的基本思想是转化，常用的方法是：

（1）an＋1－an＝f（n）型，采用叠加法．

（2）＝f（n）型，采用叠乘法．

（3）an＋1＝pan＋q（p≠0，p≠1）型，转化为等比数列解决．

[易错与防范]

1．数列是按一定“次序”排列的一列数，一个数列不仅与构成它的“数”有关，而且还与这些“数”的排列顺序有关．

2．易混项与项数是两个不同的概念，数列的项是指数列中某一确定的数，而项数是指数列的项对应的位置序号．

3．在利用数列的前n项和求通项时，往往容易忽略先求出a1，而是直接把数列的通项公式写成an＝Sn－Sn－1的形式，但它只适用于n≥2的情形．

课时分层训练（二十六）　

数列的概念与简单表示法

A组　基础达标

（建议用时：

30分钟）

一、选择题

1．在数列{an}中，a1＝1，an＝1＋（n≥2），则a5＝（　　）

A.B.

C.D.

D　[a2＝1＋＝2，a3＝1＋＝1＋＝，a4＝1＋＝3，a5＝1＋＝.]

2．下列数列中，既是递增数列又是无穷数列的是（　　）

A．1，，，，…

B．－1，－2，－3，－4，…

C．－1，－，－，－，…

D．1，，，…，

C　[根据定义，属于无穷数列的是选项A，B，C，属于递增数列的是选项C，D，故同时满足要求的是选项C.]

3．（2017·

台州期末）数列{an}的首项a1＝2，且（n＋1）an＝nan＋1，则a3的值为

（　　）

A．5B．6

C．7D．8

B　[由（n＋1）an＝nan＋1得＝，所以数列为常数列，则＝＝2，即an＝2n，所以a3＝2×

3＝6，故选B.]

4．（2017·

温州3月测试）设Sn为数列{an}的前n项和，且Sn＝（an－1）（n∈N*），则an＝（　　）

A．3（3n－2n）B．3n＋2

C．3nD．3·

2n－1

C　[当n≥2时，an＝Sn－Sn－1＝（an－1）－（an－1－1），整理，得an＝3an－1，由a1＝（a1－1），得a1＝3，∴＝3，∴数列{an}是以3为首项，3为公比的等比数列，

∴an＝3n，故选C.]

5．数列{an}满足a1＝2，an＝，其