倍长中线法的应用教案文档格式.docx

倍长中线法的应用教案文档格式.docx

《倍长中线法的应用教案文档格式.docx》由会员分享，可在线阅读，更多相关《倍长中线法的应用教案文档格式.docx（36页珍藏版）》请在冰豆网上搜索。

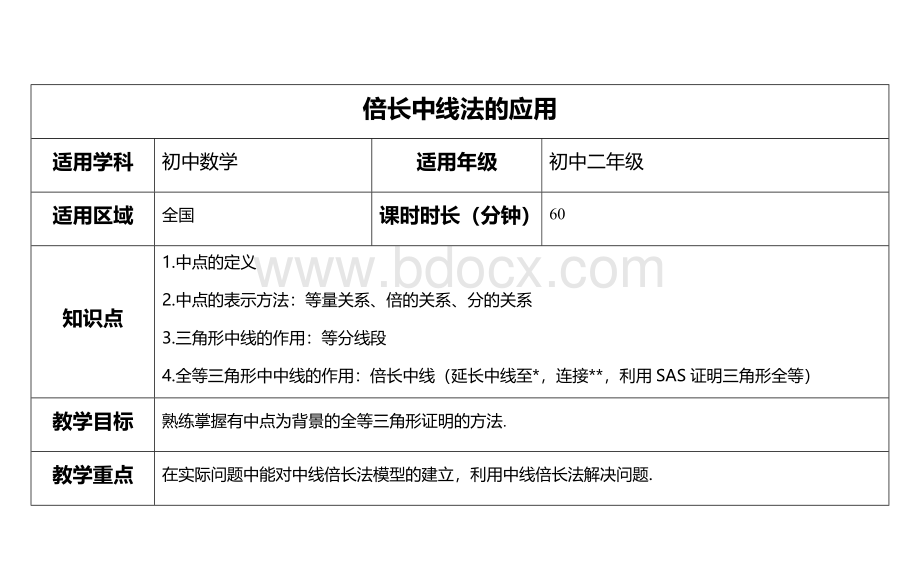
倍长中线（延长中线至*，连接**，利用SAS证明三角形全等）

教学目标

熟练掌握有中点为背景的全等三角形证明的方法.

教学重点

在实际问题中能对中线倍长法模型的建立，利用中线倍长法解决问题.

教学难点

利用中线倍长法构造全等三角形解决问题.

教学过程

一、复习引入

1.如图1，已知:

AD是BC上的中线,且DF=DE．求证:

BE∥CF．

2.如图2，AE、BC交于点M，F点在AM上，BE∥CF，BE=CF．求证：

AM是△ABC的中线．

3.如图3，AB=AC，DB=DC，F是AD的延长线上的一点。

求证：

BF=CF

4.如图4：

AB=CD，AE=DF，CE=FB。

AF=DE．

5.已知：

如图5所示，AB＝AD，BC＝DC，E、F分别是DC、BC的中点，求证：

AE＝AF．

D

B

Cc

A

F

E

图1图2图3图4图5

二、知识讲解

考点1

证明三角形全等的方法：

SAS

考点2

证明线段中的不等关系：

在三角形中，两边之和大于第三边，两边之差小于第三边.

考点3

平行线的性质：

①两直线平行,同位角相等.

②两直线平行,内错角相等.

③两直线平行,同旁内角互补.

三、例题精析

考点一证明线段中的不等关系

例1已知：

中，,是中线．

（1）求证：

．

（2）边上的中线AM的长的取值范围是什么？

【规范解答】如图所示，延长到，使，连结，

∵AM为BC中线，∴BM＝MC

在△ACM和△DBM中

∴≌（SAS），∴

在中，，∴∴

【总结与反思】①将AM边放在某个三角形中，利用三边关系求出取值范围；

②中线倍长法的具体应用：

延长AM至D，使DM=AM，连接BD；

利用SAS证明三角形全等；

③将线段AC转换成BD，在△ABD中利用三边关系求出2AM取值范围.

考点二证明两个角相等

例2如图，在中，交于点，点是中点，交的延长线于点，交于点，

若，求证：

为的角平分线．

【规范解答】延长到点，使，连结．

在和中

∴∴，∴，

而,∴

又∵,∴，

∴,∴为的角平分线．

【总结与反思】题中E为BC中点，考虑用中线倍长法得到，把CF线段转移到中，然后根据等腰三角形的性质及平行线的性质转化角得到结论。

考点三证明线段之间的关系

例3如图，已知在中，是边上的中线，是上一点，延长交于，，

求证：

【规范解答】延长到，使，连结

∵，，

∴

∴．

又∵，∴

∴，∴．

【总结与反思】作倍长AD，得到，可以把AC转移到△BDG中，利用等腰的性质得到两边相等。

四、课堂运用

【基础】

1、如图，在△ABC中，AC=5，中线AD=7，则AB边的取值范围是（）

A.2＜AB＜12B.4＜AB＜12C.9＜AB＜19D.10＜AB＜19

【答案】C

【规范解答】延长AD至E，使DE=AD，连接CE，可先证明△ABD≌△ECD，则AB=CE，在△ACE中，根据三角形的三

边关系，得AE-AC＜CE＜AE+AC，即9＜CE＜19.则9＜AB＜19.故选C.

2、已知为的中线，，的平分线分别交于、交于．求证：

【规范解答】延长到，使，连结、．

在三角形和中

≌，∴，

又∵，的平分线分别交于、交于，

∴，

利用证明≌，∴，

在中，，∴．

3、如图，在△ABC中，D是BC边的中点，E是AD上一点，BE＝AC，BE的延长线交AC于点F，

求证：

∠AEF=∠EAF

【规范解答】延长AD到G，使DG=AD，连结BG．

∵D是BC中点，∴BD=CD

在△ACD和△BGD中

△ACD≌△BGD，∴BG=AC，∠EAF=∠BGE.

∵BE=AC,∴BE=BG

∴∠BEG=∠BGE,∴∠BEG=∠AEF

∴∠AEF=∠EAF.

4、如图，点是中点，，求证：

【规范解答】延长AD到F，使EF=DG，连结CF．

∵E是BC中点，∴BE=CE

在△ABE和△CEF中

△ABE≌△CEF，∴AB=CF，∠BAE=∠CFE

∵∠BAE=∠CDE，∴∠CFE=∠CDE∴CD=CF

∴AB=CD.

【拔高】

1、如图所示，，是的中点，，，求证．

【规范解答】如图所示，设交于，倍长中线到，连接交于点，交于点．

容易证明

则，，从而，

而，，故

从而，故

而

故，亦即．

2、已知△ABC，，D，E分别是AB及AC延长线上的一点，且BD=CE，连接DE交底BC于G，

求证GD=GE．

【规范解答】

法

（一）：

过E作EF∥AB，交BC的延长线于F，则∠B=∠F

∵∠3=∠4，∠3=∠B∴∠4=∠F

∴CE=EF在△GEF与△GDB中，

∴△GFE≌△GBD∴

证明

（二）：

过D，E分别作直线DK⊥CB，EF⊥CB

∵∠1=∠2∠2=∠B∴∠1=∠B

又∵BD=CE∴Rt△BDK≌△CEF∴DK=EF

又∵∠3=∠4．∴Rt△DKG≌Rt△EFG∴GD=GE

证明（三）：

过D点作DK∥AC交BC于K，过D点作DF∥BC交AC于F

∴四边形DKCF是开行四边形

∴DK=FC∠1=∠C

∵∠C=∠B∴∠1=∠B

∴DB=DK=CE=CF

∴C是EF中点，∴BC∥DF

∴G是DE中点，∴DG=EG

课程小结

1.三角形全等证明的方法，注意两次全等的问题；

2.有中点为背景参与的问题，常见思路是“中线倍长法”.