中考专题复习最短路径问题Word文件下载.doc

中考专题复习最短路径问题Word文件下载.doc

《中考专题复习最短路径问题Word文件下载.doc》由会员分享，可在线阅读，更多相关《中考专题复习最短路径问题Word文件下载.doc（6页珍藏版）》请在冰豆网上搜索。

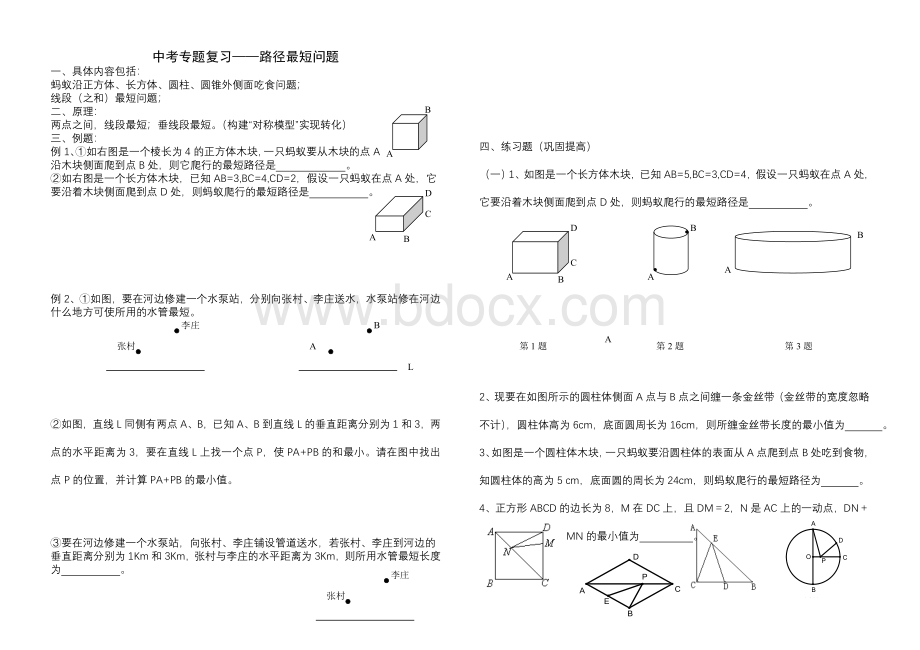
例2、①如图，要在河边修建一个水泵站，分别向张村、李庄送水，水泵站修在河边什么地方可使所用的水管最短。

②如图，直线L同侧有两点A、B，已知A、B到直线L的垂直距离分别为1和3，两点的水平距离为3，要在直线L上找一个点P，使PA+PB的和最小。

请在图中找出点P的位置，并计算PA+PB的最小值。

③要在河边修建一个水泵站，向张村、李庄铺设管道送水，若张村、李庄到河边的垂直距离分别为1Km和3Km，张村与李庄的水平距离为3Km，则所用水管最短长度为。

四、练习题（巩固提高）

（一）1、如图是一个长方体木块，已知AB=5,BC=3,CD=4，假设一只蚂蚁在点A处，它要沿着木块侧面爬到点D处，则蚂蚁爬行的最短路径是。

第3题

第2题

第1题

2、现要在如图所示的圆柱体侧面A点与B点之间缠一条金丝带（金丝带的宽度忽略不计），圆柱体高为6cm，底面圆周长为16cm，则所缠金丝带长度的最小值为。

3、如图是一个圆柱体木块，一只蚂蚁要沿圆柱体的表面从A点爬到点B处吃到食物，知圆柱体的高为5cm，底面圆的周长为24cm，则蚂蚁爬行的最短路径为。

4、正方形ABCD的边长为8，M在DC上，且DM＝2，N是AC上的一动点，DN＋MN的最小值为。

第4题第5题第6题第7题

5、在菱形ABCD中，AB=2，∠BAD=60°

，点E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值为。

⌒

6、如图，在△ABC中，AC＝BC＝2，∠ACB＝90°

，D是BC边的中点，E是AB边上一动点，则EC＋ED的最小值为_______。

7、AB是⊙O的直径，AB=2，OC是⊙O的半径，OC⊥AB，点D在AC上，AD=2CD，点P是半径OC上的一个动点，则AP+PD的最小值为_______。

（二）8、如图，点P关于OA、OB的对称点分别为C、D，连接CD，交OA于M，交OB于N，若CD＝18cm，则△PMN的周长为________。

9、已知，如图DE是△ABC的边AB的垂直平分线，D为垂足，DE交BC于E，且AC＝5，BC＝8，则△AEC的周长为__________。

10、已知，如图，在△ABC中，AB＜AC，BC边上的垂直平分线DE交BC于点D，交AC于点E，AC＝8，△ABE的周长为14，则AB的长。

11、如图，在锐角△ABC中，AB＝4，∠BAC＝45°

，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是____．

12、在平面直角坐标系中，有A（3，－2），B（4，2）两点，现另取一点C（1，n），当n=时，AC+BC的值最小．

第11题第14题第15题

13、△ABC中，∠C=90°

，AB=10，AC=6,BC=8,过AB边上一点P作PE⊥AC于E，PF⊥BC于F，E、F是垂足，则EF的最小值等于．

14、如图，菱形ABCD中，AB=2,∠BAD=60°

，点E、F、P分别是AB、BC、AC上的动点，则PE+PF的最小值为___________.

15、如图，村庄A、B位于一条小河的两侧，若河岸a、b彼此平行，现在要建设一座与河岸垂直的桥CD，问桥址应如何选择，才能使A村到B村的路程最近？

16、一次函数y=kx+b的图象与x、y轴分别交于点A（2，0），B（0，4）．

（1）求该函数的解析式；

（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC＋PD的最小值，并求取得最小值时P点坐标．

（三）16、如图，已知∠AOB内有一点P，试分别在边OA和OB上各找一点E、F，使得△PEF的周长最小。

试画出图形，并说明理由。

17、如图，直线l是第一、三象限的角平分线．

实验与探究：

（1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（－2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：

B′、C′；

归纳与发现：

（2）结合以上三组点的坐标，你会发现：

坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为；

运用与拓广：

（3）已知两点D（1，－3）、E（－1，－4），试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．

18、几何模型：

条件：

如图，A、B是直线L同旁的两个定点．问题：

在直线L上确定一点P，使PA+PB的值最小．

方法：

作点关于直线的对称点，连结交于点，则的值最小（不必证明）．

模型应用：

（1）如图1，正方形的边长为2，为的中点，是上一动点．连结，由正方形对称性可知，与关于直线对称．连结交于，则的最小值是___________；

（2）如图2，的半径为2，点在上，，，是上一动点，求的最小值；

O

P

R

Q

图3

（3）如图3，∠AOB=45°

，P是∠AOB内一点，PO=10，Q、R分别是OA、OB上的动点，求△PQR周长的最小值．

图2

E

图1

′

l

19、问题探究

（1）如图①，四边形是正方形，，为边的中点，为上的一个动点，求的最小值；

（2）如图②，若四边形是菱形，，，为边上的一个动点，为上的一个动点，求的最小值；

问题解决（3）如图③，若四边形ABCD是矩形，，，为边上的一个动点，为上的一个动点，求的最小值；

20.如图，在直角坐标系中，点A的坐标为（-2，0），连结0A，将线段OA绕原点O顺时针旋转120。

，得到线段OB.

（1）求点B的坐标；

（2）求经过A、O、B三点的抛物线的解析式；

（3）在

（2）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？

若存在，求出点C的坐标；

若不存在，请说明理由.（注意：

本题中的结果均保留根号）

解：

（1）过点B作BD⊥轴于点D，由已知可得：

OB=OA=2，∠BOD=60。

.在Rt△OBD中，∠ODB=90。

，∠OBD=30。

.

∴OD=1，DB=

∴点B的坐标是（1，）.

（2）设所求抛物线的解析式为，由已知可得：

解得：

∴所求抛物线解析式为

（3）存在.

由配方后得：

∴抛物线的对称轴为=－1.

（也写用顶点坐标公式求出）

∵OB=2，要使△BOC的周长最小，必须BC+CO最小.

∵点O与点A关于直线=－1对称，有CO=CA.

△BOC的周长=OB+BC+CO=OB+BC+CA.

∴当A、C、B三点共线，即点C为直线AB与抛物线对称轴的交点时，BC+CA最小，此时△BOC的周长最小.

设直线AB的解析式为

∴直线AB的解析式为

当=－1时，∴所求点C的坐标为（－1，）.

21、D

x

y

如图，抛物线的顶点P的坐标为，交x轴于A、B两点，交y轴于点．

（1）求抛物线的表达式．

（2）把△ABC绕AB的中点E旋转180°

，得到四边形ADBC．

判断四边形ADBC的形状，并说明理由．

（3）试问在线段AC上是否存在一点F，使得△FBD的周长最小，

若存在，请写出点F的坐标；

若不存在，请说明理由．

（1）由题意知

解得，-------------3分

（列出方程组给1分，解出给2分）

∴抛物线的解析式为-----------4分

（2）设点A（，0），B（，0），则，

解得-------------5分

∴∣OA∣＝1，∣OB∣＝3．又∵tan∠OCB＝

∴∠OCB＝60°

，同理可求∠OCA＝30°

．∴∠ACB＝90°

----------6分

由旋转性质可知AC＝BD，BC＝AD

∴四边形ADBC是平行四边形----------------------------7分

又∵∠ACB＝90°

．∴四边形ADBC是矩形--------------------------8分

（3）延长BC至N，使．假设存在一点F，使△FBD的周长最小．

即最小．

∵DB固定长．∴只要FD+FB最小．又∵CA⊥BN

∴FD+FB＝FD+FN．

∴当N、F、D在一条直线上时，FD+FB最小．---------------------10分

又∵C为BN的中点，∴（即F为AC的中点）．

又∵A（－1，0），C（0，－）∴点F的坐标为F（，）

∴存在这样的点F（，），使得△FBD的周长最小．---12分

22.已知：

直线与轴交于A，与轴交于D，抛物线与直线交于A、E两点，与轴交于B、C两点，且B点坐标为（1，0）．

（1）求抛物线的解析式；

（2）动点P在轴上移动，当△PAE是直角三角形且以P为直角顶点时，求点P的坐标．

（3）在抛物线的对称轴上找一点M，使的值最大，求出点M的坐标．

答案：

（1）将A（0，1）、B（1，0）坐标代入得

解得

∴抛物线的解折式为．3分

（2）设点E的横坐标为m，则它的纵坐标为，

则E（，）．

又∵点E在直线上，E

F

∴．

解得（舍去），．

∴E的坐标为（4，3）．4分

过E作轴于，设P（b,0）．

由，得．

．

由得．

解得，．

∴此时的点P的坐标为（1，0）或（3，0）．6分

（3）抛物线的对称轴为．∵B、C关于对称，∴．

要使最大，即是使最大．8分

由三角形两边之差小于第三边得，当A、B、M在同一直线上时的值最大．

易知直线AB的解折式为．

∴由得∴M（，－）．10分