4、费马点、利用旋转变换求线段和最值T文档格式.docx

4、费马点、利用旋转变换求线段和最值T文档格式.docx

《4、费马点、利用旋转变换求线段和最值T文档格式.docx》由会员分享，可在线阅读，更多相关《4、费马点、利用旋转变换求线段和最值T文档格式.docx（7页珍藏版）》请在冰豆网上搜索。

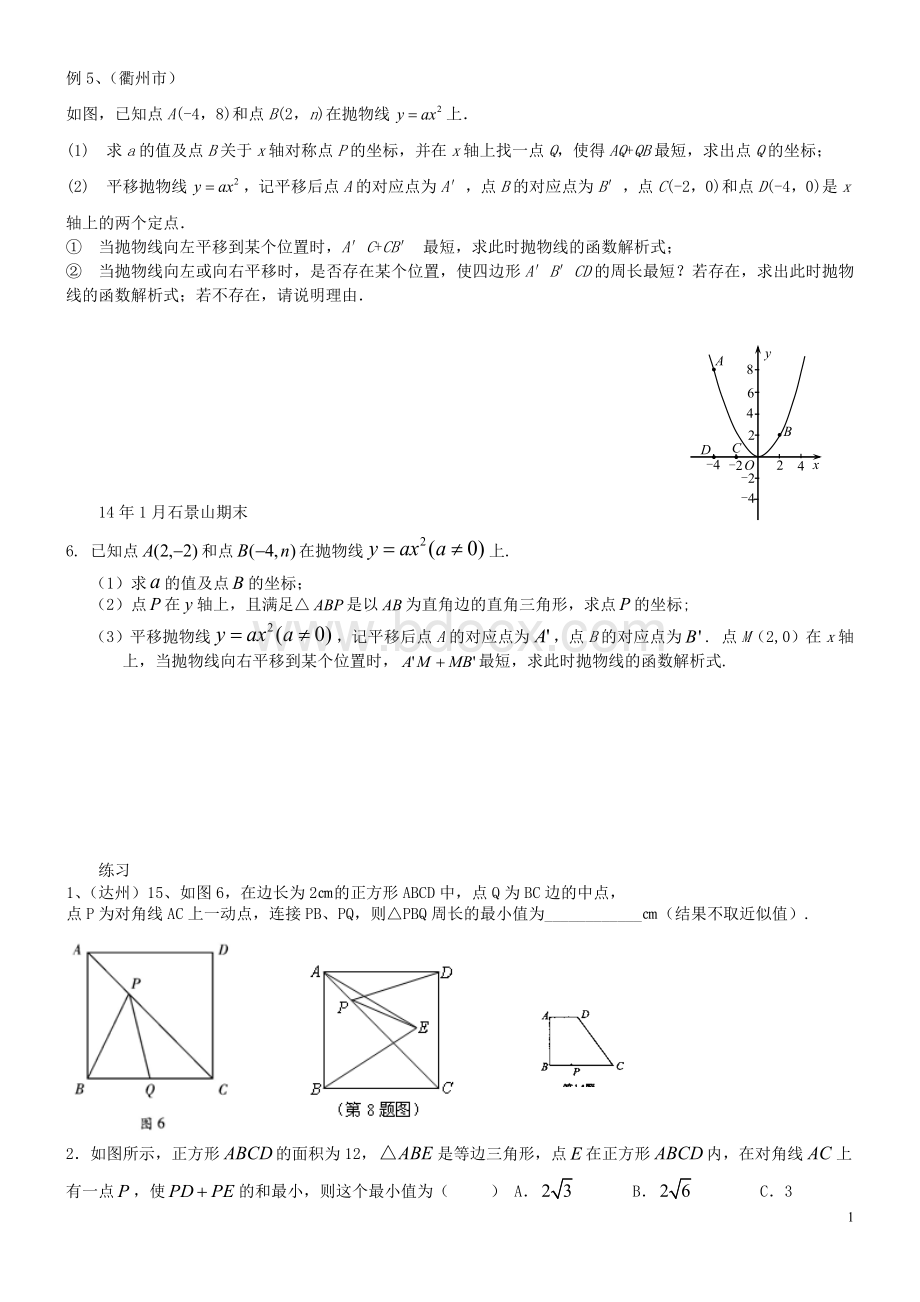
O

-4

y

6

B

C

D

14年1月石景山期末

6.已知点和点在抛物线上.

（1）求的值及点的坐标；

（2）点在轴上，且满足△是以为直角边的直角三角形，求点的坐标;

（3）平移抛物线，记平移后点A的对应点为，点B的对应点为.点M（2,0）在x轴上，当抛物线向右平移到某个位置时，最短，求此时抛物线的函数解析式.

练习

1、（达州）15、如图6，在边长为2㎝的正方形ABCD中，点Q为BC边的中点，

点P为对角线AC上一动点，连接PB、PQ，则△PBQ周长的最小值为____________㎝（结果不取近似值）.

2．如图所示，正方形的面积为12，是等边三角形，点在正方形内，在对角线上有一点，使的和最小，则这个最小值为（）A．B．C．3D．

3、滨州市中考第24题

如图1，在平面直角坐标系中，抛物线y＝ax2＋bx＋c经过A（－2,－4）、O（0,0）、B（2,0）三点．

（1）求抛物线y＝ax2＋bx＋c的解析式；

（2）若点M是该抛物线对称轴上的一点，求AM＋OM的最小值．

4、山西省中考第26题

如图1，在平面直角坐标系中，抛物线y＝－x2＋2x＋3与x轴交于A、B两点，与y轴交于点C，点D是抛物线的顶点．

（1）求直线AC的解析式及B、D两点的坐标；

（2）点P是x轴上的一个动点，过P作直线l//AC交抛物线于点Q．试探究：

随着点P的运动，在抛物线上是否存在点Q，使以A、P、Q、C为顶点的四边形是平行四边形？

若存在，请直接写出符合条件的点Q的坐标；

若不存在，请说明理由；

（3）请在直线AC上找一点M，使△BDM的周长最小，求出点M的坐标．图1

满分解答

5.（年山东聊城）已知△ABC中，边BC的长与BC边上的高的和为20．

（1）写出△ABC的面积y与BC的长x之间的函数关系式，并求出面积为48时BC的长；

（2）当BC多长时，△ABC的面积最大？

最大面积是多少？

（3）当△ABC面积最大时，是否存在其周长最小的情形？

如果存在，请说出理由，并求出其最小周长；

如果不存在，请给予说明．

6.（江苏苏州）如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，），点C的坐标为（，0），点P为斜边OB上的一动点，则PA＋PC的最小值为【　　】

A． B．C． D．2

7.（已知点D与点A（8，0），B（0，6），C（a，－a）是一平行四边形的四个顶点，则CD长的最小值为.

8.如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是　　．

9.如图，抛物线y=ax2+bx+c（a≠0）的图象过点C（0，1），顶点为Q（2，3），点D在x轴正半轴上，且OD=OC．

（1）求直线CD的解析式；

（2）求抛物线的解析式；

（3）将直线CD绕点C逆时针方向旋转45°

所得直线与抛物线相交于另一点E，求证：

△CEQ∽△CDO；

（4）在（3）的条件下，若点P是线段QE上的动点，点F是线段OD上的动点，问：

在P点和F点移动过程中，△PCF的周长是否存在最小值？

若存在，求出这个最小值；

一、费马点、利用旋转变换求线段和最值

费马点

编辑本段费马点定义

　　在一个多边形中，到每个顶点距离之和最小的点叫做这个多边形的费马点。

　　在平面三角形中:

（1）.三内角皆小于120°

的三角形，分别以AB,BC,CA，为边，向三角形外侧做正三角形ABC1,ACB1,BCA1,然后连接AA1,BB1,CC1,则三线交于一点P,则点P就是所求的费马点.

（2）.若三角形有一内角大于或等于120度,则此钝角的顶点就是所求.

　　（3）当△ABC为等边三角形时,此时外心与费马点重合

（1）等边三角形中BP=PC=PA，BP、PC、PA分别为三角形三边上的高和中线、三角上的角分线。

是内切圆和外切圆的中心。

△BPC≌△CPA≌△PBA。

（2）当BC=BA但CA≠AB时，BP为三角形CA上的高和中线、三角上的角分线。

编辑本段证明

（1）费马点对边的张角为120度。

　　△CC1B和△AA1B中,BC=BA1,BA=BC1,∠CBC1=∠B+60度=∠ABA1,

　　△CC1B和△AA1B是全等三角形,得到∠PCB=∠PA1B

　　同理可得∠CBP=∠CA1P

　　由∠PA1B+∠CA1P=60度，得∠PCB+∠CBP=60度,所以∠CPB=120度

　　同理,∠APB=120度，∠APC=120度

（2）PA+PB+PC=AA1

　　将△BPC以点B为旋转中心旋转60度与△BDA1重合，连结PD，则△PDB为等边三角形，所以∠BPD=60度

　　又∠BPA=120度，因此A、P、D三点在同一直线上，

　　又∠CPB=∠A1DB=120度，∠PDB=60度，∠PDA1=180度，所以A、P、D、A1四点在同一直线上，故PA+PB+PC=AA1。

　　（3）PA+PB+PC最短

　　在△ABC内任意取一点M（不与点P重合），连结AM、BM、CM，将△BMC以点B为旋转中心旋转60度与△BGA1重合，连结AM、GM、A1G（同上），则AA1<

A1G+GM+MA=AM+BM+CM.所以费马点到三个顶点A、B、C的距离最短。

　　平面四边型费马点

　　平面四边型中费马点证明相对于三角型中较为简易，也较容易研究。

（1）在凸四边型ABCD中，费马点为两对角线AC、BD交点P。

（2）在凹四边型ABCD中，费马点为凹顶点D（P）。

7（自编）

已知O点坐标为（0，0），A点坐标为（8，0），B点坐标为（0，8），在平面直角坐标系上确定点P，使OP＋AP＋BP最小。

并求出点P坐标和OP＋AP＋BP的最小值。

8．（自编）

已知O点坐标为（0，0），A点坐标为（5，0），B点坐标为（，），在平面直角坐标系上确定点P，使OP＋AP＋BP最小。

9、若P为所在平面上一点，且，则点叫做的费马点.

（1）若点为锐角的费马点，且，则的值为________；

（2）如图，在锐角外侧作等边′连结′.

求证：

′过的费马点，且′=.

25.如图，在平面直角坐标系中，点的坐标为，点在轴的正半轴上，，为△的中线，过、两点的抛物线与轴相交于、两点（在的左侧）.

（1）求抛物线的解析式；

（2）等边△的顶点、在线段上，求及的长；

（3）点为△内的一个动点，设，请直接写出的最小值,以及取得最小值时，线段的长.

（备用图）

13通州

24．已知：

，，以AB为一边作等边三角形ABC.使C、D两点落在直线AB的两侧.

（1）如图，当∠ADB=60°

时，求AB及CD的长；

（2）当∠ADB变化，且其它条件不变时，求CD的最大值，及相应∠ADB的大小.

D B

1房山28．如图1，已知线段BC=2，点B关于直线AC的对称点是点D，点E为射线CA上一点，且ED=BD，连接DE，BE.

（1）依题意补全图1，并证明：

△BDE为等边三角形；

（2）若∠ACB=45°

，点C关于直线BD的对称点为点F，连接FD、FB.将△CDE绕点D顺时针旋转α度（0°

＜α＜360°

）得到△，点E的对应点为E′，点C的对应点为点C′.

①如图2，当α=30°

时，连接．证明：

=；

　　②如图3，点M为DC中点，点P为线段上的任意一点，试探究：

在此旋转过程中，线段PM长度的取值范围？

图1

图2

图3

2顺义28．如图，△ABC中，AB=AC，点P是三角形右外一点，且∠APB=∠ABC．

（1）如图1，若∠BAC=60°

，点P恰巧在∠ABC的平分线上，PA=2，求PB的长；

（2）如图2，若∠BAC=60°

，探究PA，PB，PC的数量关系，并证明；

（3）如图3，若∠BAC=120°

，请直接写出PA，PB，PC的数量关系．

7