七年级列方程解应用题分类练习Word格式文档下载.doc

七年级列方程解应用题分类练习Word格式文档下载.doc

《七年级列方程解应用题分类练习Word格式文档下载.doc》由会员分享，可在线阅读，更多相关《七年级列方程解应用题分类练习Word格式文档下载.doc（6页珍藏版）》请在冰豆网上搜索。

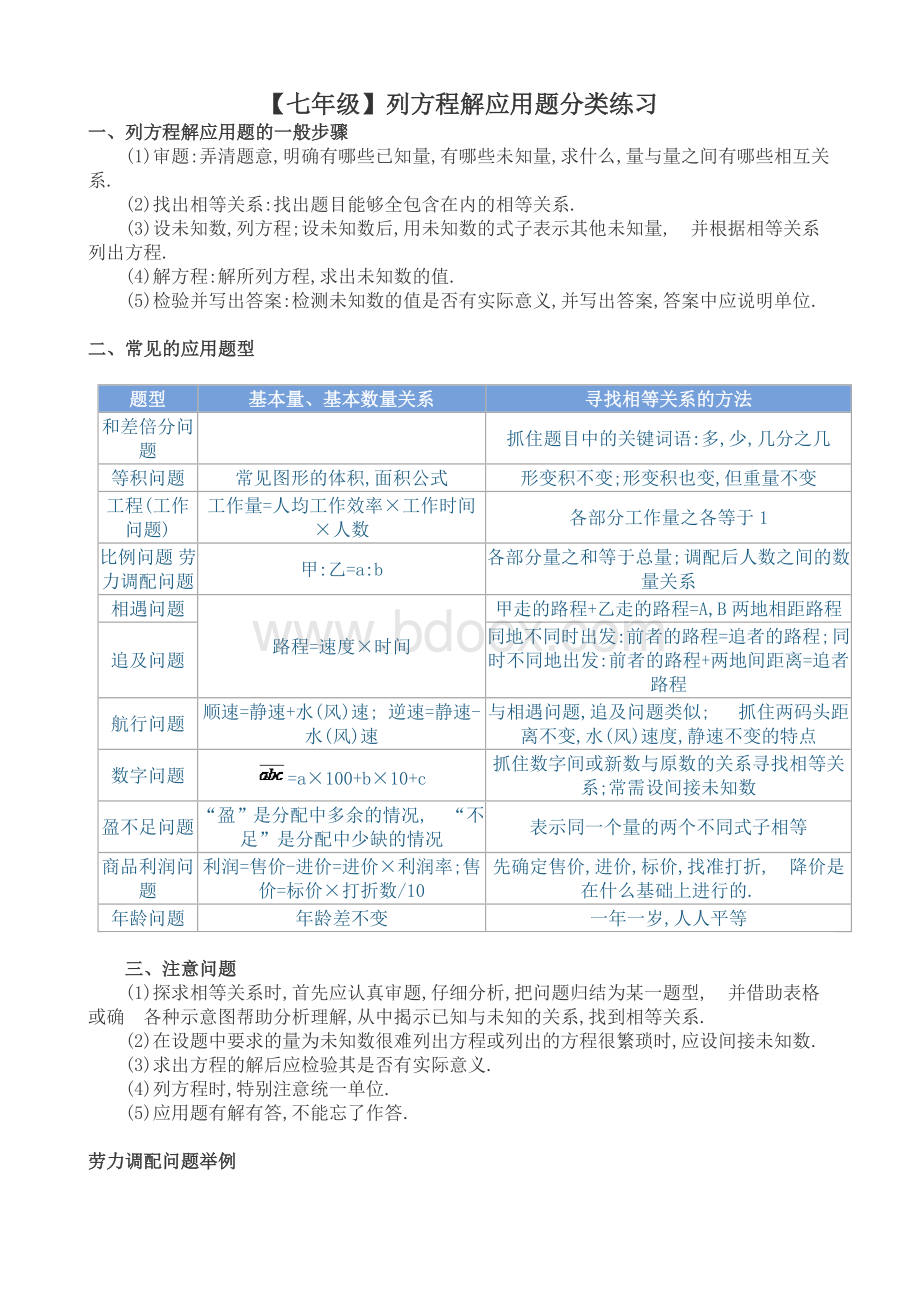
等积问题

常见图形的体积,面积公式

形变积不变;

形变积也变,但重量不变

工程（工作问题）

工作量=人均工作效率×

工作时间×

人数

各部分工作量之各等于1

比例问题劳力调配问题

甲:

乙=a:

b

各部分量之和等于总量;

调配后人数之间的数量关系

相遇问题

路程=速度×

时间

甲走的路程+乙走的路程=A,B两地相距路程

追及问题

同地不同时出发:

前者的路程=追者的路程;

同时不同地出发:

前者的路程+两地间距离=追者路程

航行问题

顺速=静速+水（风）速;

逆速=静速-水（风）速

与相遇问题,追及问题类似;

抓住两码头距离不变,水（风）速度,静速不变的特点

数字问题

=a×

100+b×

10+c

抓住数字间或新数与原数的关系寻找相等关系;

常需设间接未知数

盈不足问题

“盈”是分配中多余的情况, 

“不足”是分配中少缺的情况

表示同一个量的两个不同式子相等

商品利润问题

利润=售价-进价=进价×

利润率;

售价=标价×

打折数/10

先确定售价,进价,标价,找准打折, 

降价是在什么基础上进行的.

年龄问题

年龄差不变

一年一岁,人人平等

　　三、注意问题

（1）探求相等关系时,首先应认真审题,仔细分析,把问题归结为某一题型, 

并借助表格

或确 

各种示意图帮助分析理解,从中揭示已知与未知的关系,找到相等关系.

（2）在设题中要求的量为未知数很难列出方程或列出的方程很繁琐时,应设间接未知数.

　　（3）求出方程的解后应检验其是否有实际意义.

　　（4）列方程时,特别注意统一单位.

　　（5）应用题有解有答,不能忘了作答.

劳力调配问题举例

　　1.甲、乙两个运输队,甲队32人,乙队28人,从乙队调走x人到甲队,

（1）若甲队人数与乙队人数恰好相等,则所列方程是_________________;

（2）若甲队人数恰好是乙队人数的2倍,则所列方程是_______________;

（3）若甲队人数比乙队人数的4倍还多5人,则所列方程是_______________.

2.甲队劳动的有29人,在乙处劳动的有17人,现要赶工期,总公司另调20 

人去支援,使甲处的人数为乙处人数的2倍,应分别调往甲处、乙处各多少人?

3.甲工厂有某种原料120吨,乙工厂有同样的原料96吨,甲厂每天用原料15吨,乙厂每天用原料9吨,问多少天后,两工厂剩下的原料相等?

4.有甲、乙两个牧童，甲对乙说：

“把你的羊给我1只， 

我的羊数就是你的羊数的2倍。

”乙回答说：

“很好还是把你的羊给我1只，这样我们的羊就一样多了。

”两个牧童各有几只羊?

　　配套问题举例

1.某车间22名工人生产螺钉和螺母,每人每天平均生产1200个螺钉或2000 

个螺母,一个螺钉配两个螺母,为了使每天的产品刚好配套,应该安排工人生产?

2.用铝片做听装饮料瓶,每张铝片可制作瓶身16个或制作瓶底43个,一个瓶身与两个瓶底配成一套,现有150张铝片,用多少张铝片制瓶身,多少张铝片制瓶底可以正好制成配套的饮料?

　　等积变形问题举例

1.将棱长为0.5m的正方体钢锭,熔解成长、宽、高分别为0.4m、0.2m、0.1m 

的长方体钢锭.至少可铸成多少个?

2.用一根直径为12cm的圆柱形铝柱,铸造10只直径为12cm的铅球,问应截取多长的铝柱?

（球的体积V＝,R为球的半径

　　3.把一个边长为25cm的正方形铁丝框重新围成长方形,

（1）使得该长方形的长比宽多14cm,此时的长宽各是多少?

（2）使得该长方形的长比宽多8cm, 

此时长方形的面积是多少?

　　数字问题举例

　　1.用式子表示下列两位数或三位数:

（1）一个两位数,个位数字是a,十位数字是b:

____________

（2）一个两位数,个位数字是a,十位数字比个位数字小1:

__________

　　（3）一个两位数,个位数字是a,比十位数字小1:

__________（4）一个两位数,十位数字是a,个位数字比十位数字的2倍多3;

　　（5）一个三位数,十位数字是a,比百位数字大1,比个位数字少1.____________

2.一个两位数,个位上的数字比十位上的数字大2, 

个位与十位上的数字之和是10,求这个两位数.

3.一个两位数,个位上的数字与十位上的数字之和是7, 

若把个位与十位数字对调,则所得的两位数比原两位数大27,求这个两位数.

4.有一列数,按一定规律排列成1,-2,4,-8,16,-32……,其中某三个相邻数的和是-96,这三个数各是多少?

　　5.下图是本月的日历,用如图所示的“十字架”去框其中的五个数,若这五个数的和是60,你知道框住的是哪五个数吗?

在图中画出来,并用方程的知识进行说明.

1 

2 

3 

4 

5 

6

7 

8 

9 

10 

11 

12 

13

14 

15 

16 

17 

18 

19 

20

21 

22 

23 

24 

25 

26 

27

28 

29 

30

　行程问题举例:

时间 

V顺=V静+V水 

V顺=V静-V水

　　1.甲、乙两人登一座高山,甲每分钟登高10米,且先出发30分钟, 

乙每钟登高15米,两人同时到达山顶.甲用多少时间登山?

这座山有多高?

2.学校田径队的小刚在400米跑测试时,先以6米/秒的速度跑完了大部分路程, 

最后以8米/秒的速度冲刺激到达终点,成绩为1分零5秒,问小刚在冲刺阶段花了多少时间?

3.从甲地到乙地,公共汽车原需行驶7小时,开通高速公路后,车速平均每小时增加20千米,只需5小时即可到达,求甲、乙两地的路程.

4.小明原计划骑车以12千米/时的速度,由A地去B地, 

这样便可在规定时间到达B地,但因故将原计划出发时间推迟了20分钟,只好以15千米/时的速度前进, 

结果比规定时间早4分钟到达B地,求A、B两地的距离.

5.一架飞机在两城之间飞行,风速为24千米/时,顺风飞行需要2小时50分, 

逆风飞行需要3小时,求无风时的飞机的航行速度和两城之间的路程?

　　6.A、B两地相距480千米,一列慢车以每小时60千米的速度从A地开出,一列快车以65千米/时的速度从B地开出.

（1）若两车同时开出,相向而行,多少时间相遇?

（2）若慢车先开出1小时,两车同向而行,快车开出多少小时追上慢长?

　　（3）右两车同时开出,相背而行,多少小时后两车相距620千米?

　　（4）若慢车先开出1小时,相向而行,慢车开出多少小时后两车相距620千米?

　　工程问题举例:

工作量=工作效率×

工作时间=人均工效×

工时×

1.食堂有煤若干吨,原来每天烧煤3吨,用去15吨后,改进设备, 

耗煤量改为原来的一半,结果多烧了10天,求原存煤量.

2.一项工程,甲工程队单独做40天可以完成,乙工程队单独做80天可以完成, 

现由甲先单独做10天,然后与乙共同完成余下的工程,问甲工程队一共做了多少天?

3.某工程,甲、乙、丙单独做分别要10天、12天、20天完成。

现甲独做2天后, 

由乙独 

做若干天后,然后甲、乙、丙又合作2天才能把全部工程干完, 

问乙一共做了多少天?

4.某水池有一进水管和一放水管.若单独开进水管6小时可注满水池, 

若单独开放水管,8小时可放完一池水,若同时开两小管,那么多少小时可注满水池的一半?

5.一项工作,由1人做要40小时完成.现计划由一部分人先做4小时,再增加2人一起做8小时,完成这项工作的,假设这些人的工作效率相同, 

具体应先安排多少人工作?

　　销售盈亏问题举例:

销售额=单价×

销售量,商品利润=售价-进价=利润率×

进价

1.某商品售价为900元一件,为了适应市场竞争,商场按九折降价并让利40 

元销售,仍可获利10%,求这种商品进价为多少元?

2.某商品因换季准备打折出售,如果按标价的七五折出售将赔25元,若按标价的九折出售将赚20元,问这种商品的标价是多少元?

3.一种产品,每件成本价为400元,销售价为510元,为了进一步扩大市场,决定降低售价的同时降低生产成本,预计每件售价降低4%,销售量将提高10%,要使销售利润保持不变,该产品每件的成本应降低多少元?

　　方案优选题举例

1.学校准备组织教师和很好学生去大洪山春游,其中教师22名,现有甲、乙两家旅行社,两家定价相同,但优惠方式不同:

甲旅行社表示教师免费,学生按八折优惠;

乙旅行社表示教师和学生一律按七五折优惠,学校领导经过核算后认为甲、 

乙旅行社的收费一样,请你算出有多少学生参加春游.

　　2.全球通手机卡收费每分钟0.20元,月租每月20元;

神州行手机卡没有月租费, 

每分钟0.4元,

（1）当一个月通话时间多少分钟时,使用这两种手机的费用相同?

（2）针对这两种手机卡,从经济角度考虑,你应如何选择?

　　4.某同学在A、B两家超市发现他看中的随身听的单价相同,书包的单价也相同,随身听和书包的单价之和为452元,且随身听的单价比书包的单价的4倍少8元.

（1）求该同学看中的随身听和书包的单价各是多少?

（2）某一载该同学上街,恰好赶上商家促销,超市A所有的商品打八折销售, 

超市B全场购物满100元返购物券20元（不足100元不返购物券,购物券全场通用）但他只带了400元钱,如果他只在一家超市购买看中的两样物品, 

你能说明他可以选择哪一家购买吗?

若两家都可以选择,在哪一家购买更省钱?

　　其它题型举例

1.（年龄问题）小新出生时父亲28岁，现在父亲的年龄是小新年龄的3倍，求现在小新的年龄？

2.（均额问题）.某班48名同学去湖上划船,一共乘坐10条船,大船坐5人, 

小船坐3人,正好全部坐满,问大船、小船各有几条?

3.（均额问题）.有一些相同的房间需要粉刷,一天3名一级技工去粉刷8个房间, 

结果其中有50m2墙面未来得及刷;

同样时间内5名二级技工粉刷了10个房间之外, 

还多刷了另外的40m2墙面.每名一级技工比二级技工每天多刷10m2墙面,求每个房间需要粉刷的墙面.

　　4.（盈不足）课外活动中,一些同学分组参加活动,原来每组8人, 

后来由于器材不够重新编组,每组12人,这样比原来少2组,求该班人数.