小学奥数知识总结手册Word文件下载.docx

小学奥数知识总结手册Word文件下载.docx

《小学奥数知识总结手册Word文件下载.docx》由会员分享，可在线阅读，更多相关《小学奥数知识总结手册Word文件下载.docx（18页珍藏版）》请在冰豆网上搜索。

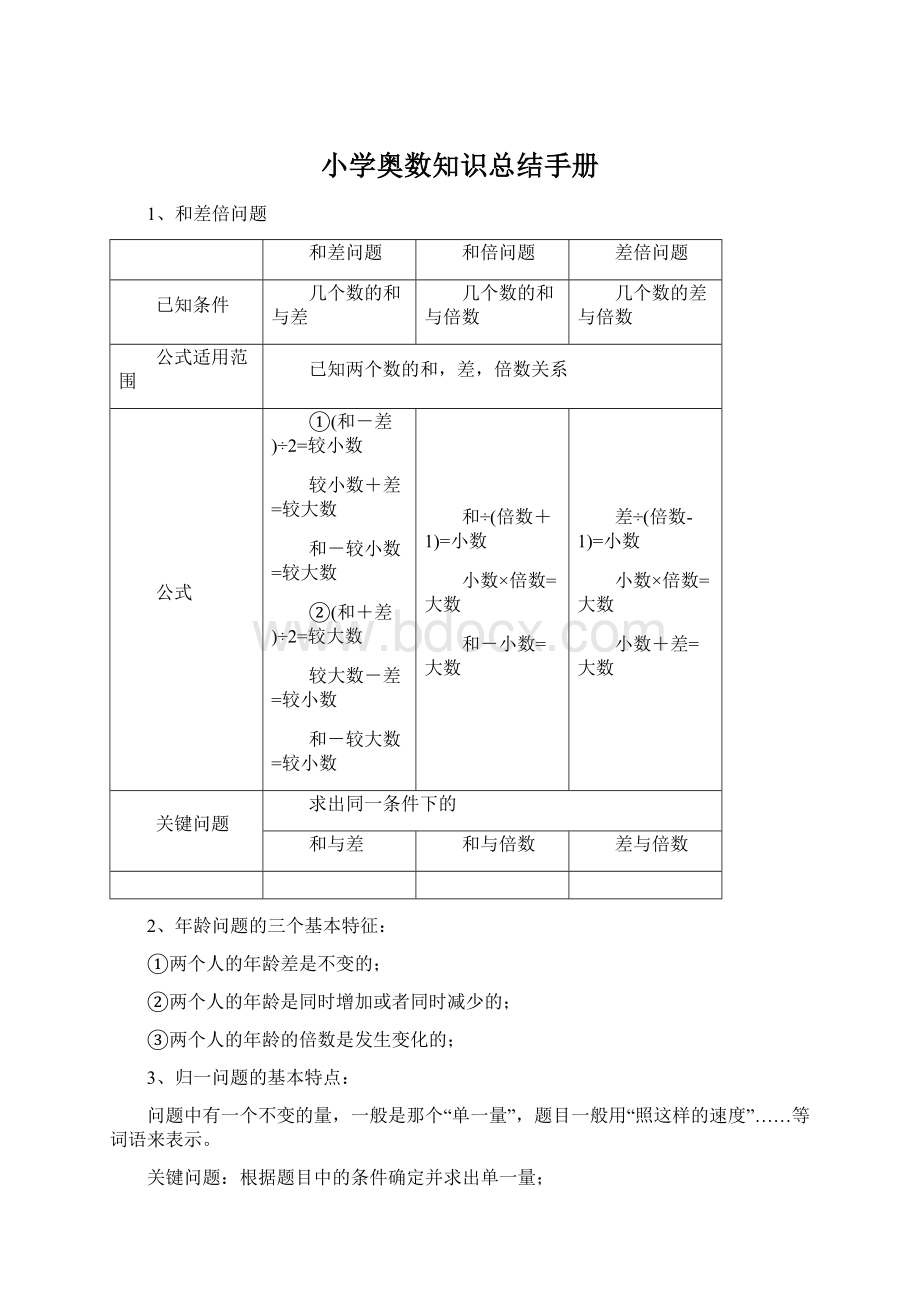
①两个人的年龄差是不变的；

②两个人的年龄是同时增加或者同时减少的；

③两个人的年龄的倍数是发生变化的；

3、归一问题的基本特点：

问题中有一个不变的量，一般是那个“单一量”，题目一般用“照这样的速度”……等词语来表示。

关键问题：

根据题目中的条件确定并求出单一量；

4、植树问题

基本类型

在直线或者不封闭的曲线上植树，两端都植树

在直线或者不封闭的曲线上植树，两端都不植树

在直线或者不封闭的曲线上植树，只有一端植树

封闭曲线上植树

基本公式

棵数=段数＋1

棵距×

段数=总长

棵数=段数－1

棵数=段数

确定所属类型，从而确定棵数与段数的关系

5、鸡兔同笼问题

基本概念：

鸡兔同笼问题又称为置换问题、假设问题，就是把假设错的那部分置换出来；

基本思路：

①假设，即假设某种现象存在（甲和乙一样或者乙和甲一样）：

②假设后，发生了和题目条件不同的差，找出这个差是多少；

③每个事物造成的差是固定的，从而找出出现这个差的原因；

④再根据这两个差作适当的调整，消去出现的差。

基本公式：

①把所有鸡假设成兔子：

鸡数＝（兔脚数×

总头数－总脚数）÷

（兔脚数－鸡脚数）

②把所有兔子假设成鸡：

兔数＝（总脚数一鸡脚数×

总头数）÷

（兔脚数一鸡脚数）

找出总量的差与单位量的差。

6、盈亏问题

一定量的对象，按照某种标准分组，产生一种结果：

按照另一种标准分组，又产生一种结果，由于分组的标准不同，造成结果的差异，由它们的关系求对象分组的组数或对象的总量．

先将两种分配方案进行比较，分析由于标准的差异造成结果的变化，根据这个关系求出参加分配的总份数，然后根据题意求出对象的总量．

基本题型：

①一次有余数，另一次不足；

总份数＝（余数＋不足数）÷

两次每份数的差

②当两次都有余数；

总份数＝（较大余数一较小余数）÷

③当两次都不足；

总份数＝（较大不足数一较小不足数）÷

基本特点：

对象总量和总的组数是不变的。

确定对象总量和总的组数。

7、牛吃草问题

假设每头牛吃草的速度为“1”份，根据两次不同的吃法，求出其中的总草量的差；

再找出造

成这种差异的原因，即可确定草的生长速度和总草量。

原草量和新草生长速度是不变的；

确定两个不变的量。

生长量=（较长时间×

长时间牛头数-较短时间×

短时间牛头数）÷

（长时间-短时间）；

总草量=较长时间×

长时间牛头数-较长时间×

生长量；

8、周期循环与数表规律

周期现象：

事物在运动变化的过程中，某些特征有规律循环出现。

周期：

我们把连续两次出现所经过的时间叫周期。

确定循环周期。

闰年：

一年有366天；

①年份能被4整除；

②如果年份能被100整除，则年份必须能被400整除；

平年：

一年有365天。

①年份不能被4整除；

②如果年份能被100整除，但不能被400整除；

9、平均数

①平均数=总数量÷

总份数

总数量=平均数×

总份数=总数量÷

平均数

②平均数=基准数＋每一个数与基准数差的和÷

基本算法：

①求出总数量以及总份数，利用基本公式①进行计算.

②基准数法：

根据给出的数之间的关系，确定一个基准数；

一般选与所有数比较接近的数或者中间数为基准数；

以基准数为标准，求所有给出数与基准数的差；

再求出所有差的和；

再求出这些差的平均数；

最后求这个差的平均数和基准数的和，就是所求的平均数，具体关系见基本公式②

10、抽屉原理

抽屉原则一：

如果把（n+1）个物体放在n个抽屉里，那么必有一个抽屉中至少放有2个物体。

例：

把4个物体放在3个抽屉里，也就是把4分解成三个整数的和，那么就有以下四种情况：

①4=4+0+0②4=3+1+0③4=2+2+0④4=2+1+1

观察上面四种放物体的方式，我们会发现一个共同特点：

总有那么一个抽屉里有2个或多于2个物体，也就是说必有一个抽屉中至少放有2个物体。

抽屉原则二：

如果把n个物体放在m个抽屉里，其中n>

m，那么必有一个抽屉至少有:

①k=[n/m]+1个物体：

当n不能被m整除时。

②k=n/m个物体：

当n能被m整除时。

理解知识点：

[X]表示不超过X的最大整数。

例[4.351]=4；

[0.321]=0；

[2.9999]=2；

构造物体和抽屉。

也就是找到代表物体和抽屉的量，而后依据抽屉原则进行运算。

11、定义新运算

定义一种新的运算符号，这个新的运算符号包含有多种基本（混合）运算。

严格按照新定义的运算规则，把已知的数代入，转化为加减乘除的运算，然后按照基本运算过程、规律进行运算。

正确理解定义的运算符号的意义。

注意事项：

①新的运算不一定符合运算规律，特别注意运算顺序。

②每个新定义的运算符号只能在本题中使用。

12、数列求和

等差数列：

在一列数中，任意相邻两个数的差是一定的，这样的一列数，就叫做等差数列。

首项：

等差数列的第一个数，一般用a1表示；

项数：

等差数列的所有数的个数，一般用n表示；

公差：

数列中任意相邻两个数的差，一般用d表示；

通项：

表示数列中每一个数的公式，一般用an表示；

数列的和：

这一数列全部数字的和，一般用Sn表示．

等差数列中涉及五个量：

a1,an,d,n,sn,,通项公式中涉及四个量，如果己知其中三个，就可求出第四个；

求和公式中涉及四个量，如果己知其中三个，就可以求这第四个。

通项公式：

an=a1+（n－1）d；

通项＝首项＋（项数一1）×

公差；

数列和公式：

sn,=（a1+an）×

n÷

2；

数列和＝（首项＋末项）×

项数÷

项数公式：

n=（an+a1）÷

d＋1；

项数=（末项-首项）÷

公差＋1；

公差公式：

d=（an－a1））÷

（n－1）；

公差=（末项－首项）÷

（项数－1）；

确定已知量和未知量，确定使用的公式；

13、二进制及其应用

十进制：

用0～9十个数字表示，逢10进1；

不同数位上的数字表示不同的含义，十位上的2表示20，百位上的2表示200。

所以234=200+30+4=2×

102+3×

10+4。

=An×

10n-1+An-1×

10n-2+An-2×

10n-3+An-3×

10n-4+An-4×

10n-5+An-6×

10n-7+……+A3×

102+A2×

101+A1×

100

注意：

N0=１；

N１=N（其中N是任意自然数）

二进制：

用0～1两个数字表示，逢2进1；

不同数位上的数字表示不同的含义。

（2）=An×

2n-1+An-1×

2n-2+An-2×

2n-3+An-3×

2n-4+An-4×

2n-5+An-6×

2n-7+……+A3×

22+A2×

21+A1×

20

An不是0就是1。

十进制化成二进制：

①根据二进制满2进1的特点，用2连续去除这个数，直到商为0，然后把每次所得的余数按自下而上依次写出即可。

②先找出不大于该数的2的n次方，再求它们的差，再找不大于这个差的2的n次方，依此方法一直找到差为0，按照二进制展开式特点即可写出。

14、加法乘法原理和几何计数

加法原理：

如果完成一件任务有n类方法，在第一类方法中有m1种不同方法，在第二类方法中有m2种不同方法……，在第n类方法中有mn种不同方法，那么完成这件任务共有：

m1+m2.......+mn种不同的方法。

确定工作的分类方法。

基本特征：

每一种方法都可完成任务。

乘法原理：

如果完成一件任务需要分成n个步骤进行，做第1步有m1种方法，不管第1步用哪一种方法，第2步总有m2种方法……不管前面n-1步用哪种方法，第n步总有mn种方法，那么完成这件任务共有：

m1×

m2.......×

mn种不同的方法。

确定工作的完成步骤。

每一步只能完成任务的一部分。

直线：

一点在直线或空间沿一定方向或相反方向运动，形成的轨迹。

直线特点：

没有端点，没有长度。

线段：

直线上任意两点间的距离。

这两点叫端点。

线段特点：

有两个端点，有长度。

射线：

把直线的一端无限延长。

射线特点：

只有一个端点；

没有长度。

①数线段规律：

总数＝1+2+3+…+（点数一1）；

②数角规律=1+2+3+…+（射线数一1）；

③数长方形规律：

个数=长的线段数×

宽的线段数：

④数长方形规律：

个数=1×

1+2×

2+3×

3+…+行数×

列数

15、质数与合数

质数：

一个数除了1和它本身之外，没有别的约数，这个数叫做质数，也叫做素数。

合数：

一个数除了1和它本身之外，还有别的约数，这个数叫做合数。

质因数：

如果某个质数是某个数的约数，那么这个质数叫做这个数的质因数。

分解质因数：

把一个数用质数相乘的形式表示出来，叫做分解质因数。

通常用短除法分解质因数。

任何一个合数分解质因数的结果是唯一的。

分解质因数的标准表示形式：

N=，其中a1、a2、a3……an都是合数N的质因数，且a1<

a2<

a3<

……<

an。

求约数个数的公式：

P=（r1+1）×

（r2+1）×

（r3+1）×

……×

（rn+1）

互质数：

如果两个数的最大公约数是1，这两个数叫做互质数。

16、约数与倍数

约数和倍数：

若整数a能够被b整除，a叫做b的倍数，b就叫做a的约数。

公约数：

几个数公有的约数，叫做这几个数的公约数；

其中最大的一个，叫做这几个数的最大公约数。

最大公约数的性质：

1、几个数都除以它们的最大公约数，所得的几个商是互质数。

2、几个数的最大公约数都是这几个数的约数。

3、几个数的公约数，都是这几个数的最大公约数的约数。

4、几个数都乘以一个自然数m，所得的积的最大公约数等于这几个数的最大公约数乘以m。

例如：

12的约数有1、2、3、4、6、12；

18的约数有：

1、2、3、6、9、18；

那么12和18的公约数有：

1、2、3、6；

那么12和18最大的公约数是：

6，记作（12，18）=6；

求最大公约数基本方法：

1、分解质因数法：

先分解质因数，然后把相同的因数连乘起来。

2、短除法：

先找公有的约数，然后相乘。

3、辗转相除法：

每一次都用除数和余数相除，能够整除的那个余数，就是所求的最大公约数。

公倍数：

几个数公有的倍数，叫做这几个数的公倍数；

其中最小的一个，叫做这几个数的最小公倍数。

12的倍数有：

12、24、36、48……；

18的倍数有：

18、36、54、72……；

那么12和18的公倍数有：

36、72、108……；

那么12和18最小的公倍数是36，记作[12，18]=36；

最小公倍数的性质：

1、两个数的任意公倍数都是它们最小公倍数的倍数。

2、两个数最大公约数与最小公倍数的乘积等于这两个数的乘积。

求最小公倍数基本方法：

1、短除法求最小公倍数；

2、分解质因数的方法

17、数的整除

一、基本概念