上海八年级上学期期末压轴题最后一道题Word文件下载.docx

上海八年级上学期期末压轴题最后一道题Word文件下载.docx

《上海八年级上学期期末压轴题最后一道题Word文件下载.docx》由会员分享，可在线阅读，更多相关《上海八年级上学期期末压轴题最后一道题Word文件下载.docx（8页珍藏版）》请在冰豆网上搜索。

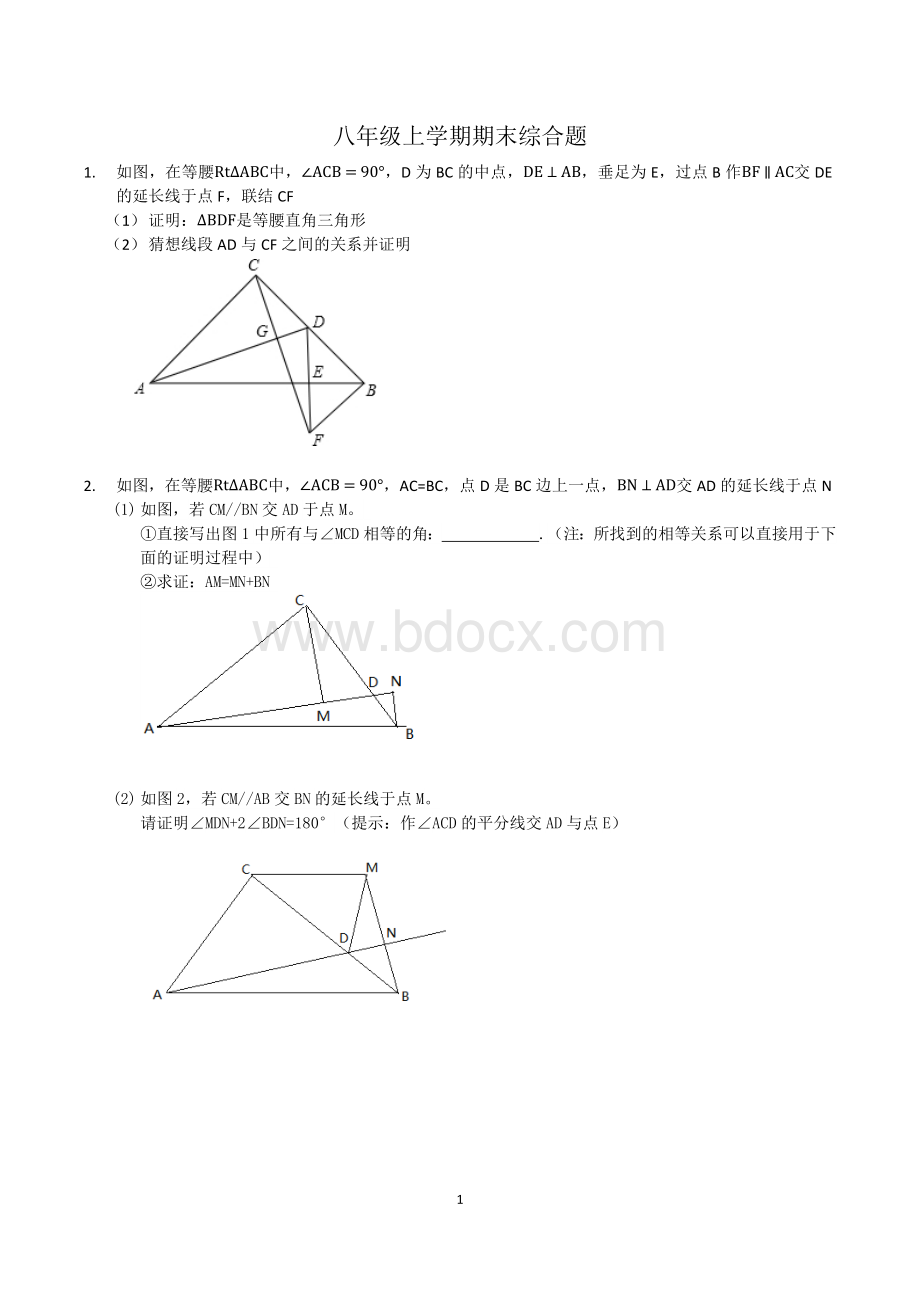
所找到的相等关系可以直接用于下面的证明过程中）

②求证：

AM=MN+BN

（2）如图2，若CM//AB交BN的延长线于点M。

请证明∠MDN+2∠BDN=180°

（提示：

作∠ACD的平分线交AD与点E）

3.如图

（1），直角梯形OABC中，∠A=90°

，AB∥CO,且AB=2，OA=2，∠BCO=60°

。

（1）求证：

OBC为等边三角形；

（2）如图

（2），OH⊥BC于点H，动点P从点H出发，沿线段HO向点O运动，动点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为1/秒。

设点P运动的时间为t秒，ΔOPQ的面积为S，求S与t之间的函数关系式，并求出t的取值范围；

（3）设PQ与OB交于点M，当OM=PM时，求t的值。

图

（2）

（备用图）

图

（1）

4.已知，点P是直角三角形ABC斜边AB上一动点（不与A，B重合），分别过A，B向直线CP作垂线，垂足分别为E，F，Q为斜边AB的中点．

（1）如图1，当点P与点Q重合时直接写出AE与BF的位置关系和QE与QF的数量关系；

（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系并证明之；

（3）如图3，当点P在线段BA（或AB）的延长线上时，此时

（2）中的结论是否成立？

请画出图形并给予证明．

5.在Rt△中,，，，点是射线CB上的一个动点，△ADE是等边三角形，点是的中点，联结．

（1）如图1，当点在线段CB上时，

①求证：

△≌△；

②联结BE，设线段，线段，求关于的函数解析式及定义域；

（2）当时，求△ADE的面积.

图1

备用图

6.如图，直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边△AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，直线DA交y轴于点E．

（1）△OBC与△ABD全等吗？

判断并证明你的结论；

（2）随着点C位置的变化，点E的位置是否会发生变化？

若没有变化，求出点E的坐标；

若有变化，请说明理由．

7.小刘同学在一次课外活动中，用硬纸片做了两个直角三角形，见图1、图2．图1中，

；

图2中，．图3是小刘同学所做的一个实验：

他将的直角边DE与的斜边AC重合在一起，并将沿AC方向移动．在移动过程中，D、E两点始终在AC边上（移动开始时点D与点A重合）．

（1）在沿AC方向移动的过程中，小刘同学发现：

F、C两点间的距离逐渐_______；

（填“不变”、“变大”或“变小”）

（2）小刘同学经过进一步研究，编制了如下问题：

问题①：

当移动至什么位置，即AD的长为多少时，F、C的连线与AB平行?

问题②：

当移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形?

请你分别完成上述两个问题的解答过程．

A

B

C

图2

F

D

E

图3

8.已知：

如图，在Rt△ABC中，∠A＝90°

，AB＝AC＝1，P是AB边上不与A点、B点重合的任意一个动点，PQ⊥BC于点Q，QR⊥AC于点R。

PQ＝BQ；

（2）设BP＝x，CR＝y，求y关于x的函数解析式，并写出定义域；

（3）当x为何值时，PR//BC。

9.如图，在长方形ABCD中，AB=8，AD=6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP=CQ。

设AP=，BE=y

（1）线段PQ的垂直平分线与BC边相交，设交点为E求y与的函数关系式及取值范围；

（2）在

（1）的条件是否存在x的值，使△PQE为直角三角形?

若存在，请求出x的值，若不存在请说明理由。

10.如图1，在中，，，，点是边上的动点（点不与点重合），过点作∥，交边于点，再把沿着动直线翻折得到，设．

（1）求的大小；

（2）当点落在斜边上时，求的值；

（3）当点落在外部时，与相交于点，如果，请直接写出关于的函数关系式及定义域．

P

Q

R

（图1）

11.在直角三角形ABC中，∠C＝90○，已知AC＝6cm，BC＝8cm。

（1）求AB边上中线CM的长；

（2）点P是线段CM上一动点（点P与点C、点M不重合），求出△APB的面积y（平方厘米）与CP的长x（厘米）之间的函数关系式并求出函数的定义域

（3）是否存在这样的点P，使得△ABP的面积是凹四边形ACBP面积的，如果存在请求出CP的长，如果不存在，请说明理由！

12.如图，在△中，∠=90°

，∠=30°

，是边上不与点A、C重合的任意一点，⊥，垂足为点，是的中点.

=；

（2）如果=，设=，=，求与的函数解析式，并写出函数的定义域；

（3）当点在线段上移动时，∠的大小是否发生变化？

如果不变，求出∠的大小；

如果发生变化，说明如何变化.

13.如图，已知长方形纸片ABCD的边AB=2，BC=3，点M是边CD上的一个动点（不与点C重合），把这张长方形纸片折叠，使点B落在M上，折痕交边AD与点E，交边BC于点F．

（1）、写出图中全等三角形；

（2）、设CM=x，AE=y，求y与x之间的函数解析式，写出定义域；

（3）、试判断能否可能等于90度？

如可能，请求出此时CM的长；

如不能，请说明理由．

14.已知中，AC=BC,,点D为AB边的中点，,DE、DF分别交AC、BC于E、F点．

（1）如图（图1），若EF∥AB．求证：

DE=DF．

（2）如图（图2），若EF与AB不平行．则问题

（1）的结论是否成立？

说明理由．

（图2）

15.如图（图1）,已知中,BC=3,AC=4,AB=5,直线MD是AB的垂直平分线，分别交AB、AC于M、D点.

（1）求线段DC的长度；

（2）如图（图2），联接CM，作的平分线交DM于N.求证:

CM＝MN.

M

N

16.在△ABC中，AD⊥BC，垂足为点D（D在BC边上），BE⊥AC，垂足为点E，M为AB边的中点，联结ME、MD、ED。

（1）当点E在AC边上时（如图1），容易证明∠EMD=2∠DAC；

当点E在CA的延长线上，请在图2中画出相应的图形，并说明“∠EMD=2∠DAC”是否还成立？

若成立，请证明；

若不成立，请说明理由；

（2）如果△MDE为正三角形，BD=4，且AE=1，求△MDE的周长．

8