《电磁场与电磁波》第四版习题集第7章导行电磁波Word格式.docx

《电磁场与电磁波》第四版习题集第7章导行电磁波Word格式.docx

《《电磁场与电磁波》第四版习题集第7章导行电磁波Word格式.docx》由会员分享，可在线阅读，更多相关《《电磁场与电磁波》第四版习题集第7章导行电磁波Word格式.docx（58页珍藏版）》请在冰豆网上搜索。

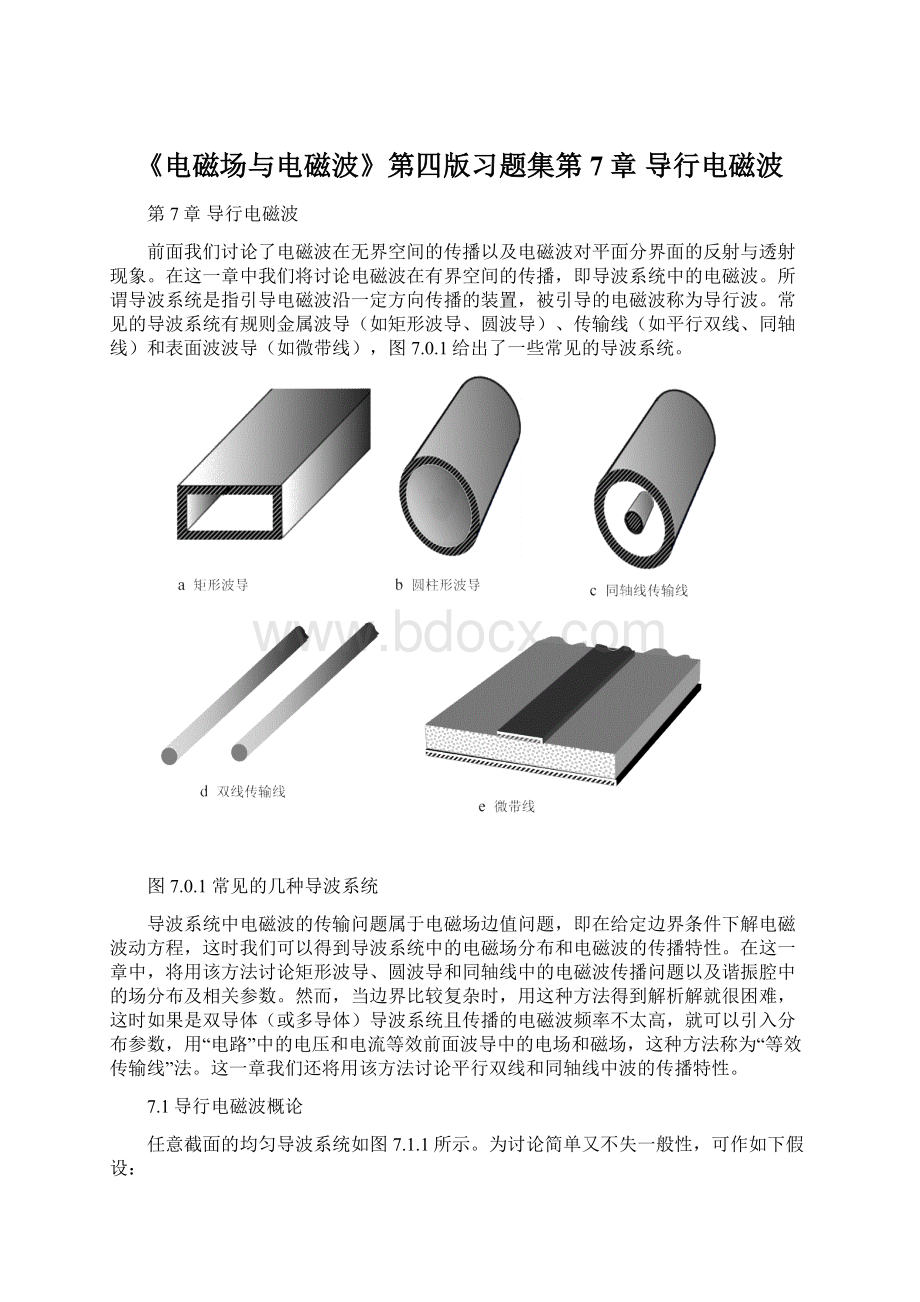
图7.1.1任意截面的均匀波导

设波导中电磁波沿+z方向传播，对于角频率为的时谐场，由假设条件

（1）和

（2）可将其电磁场量表示为

（7.1.1）

式中称为传播常数，表征导波系统中电磁场的传播特性。

为导波系统中的场分布。

而我们将进行的工作就是在不同导波系统的边界条件下求解麦克斯韦方程组，得到传播常数和相应的场分布。

由假设条件（4），讨论区域内没有源分布，则波导内的电磁场满足的麦克斯韦方程为

（7.1.2）

（7.1.3）

将以上二式在直角坐标系中展开，可得到x、y、z三个分量的6个标量方程。

（7.1.4a）

（7.1.4b）

（7.1.4c）

（7.1.4d）

（7.1.4e）

（7.1.4f）

将以上6个方程经过简单运算可将波导中的横向场分量、、、用两个纵向场分量和来表示。

得

（7.1.5a）

（7.1.5b）

（7.1.5c）

（7.1.5d）

式中

式（7.1.5a）~（7.1.5d）为均匀导波系统中纵向场分量与横向场分量的关系式。

由该关系式可知，波导中的横向场分量可由纵向场分量确定。

我们还可以根据纵向场分量和的存在与否，对波导中传播的电磁波进行分类。

（1）横电磁波又称为TEM波，这种波既无分量又无分量。

（2）横磁波又称为TM波，这种波包含了非零的分量，但。

（3）横电波又称为TE波，这种波包含了非零的分量，但。

7.1.1.TEM波

对于TEM波，因为和，所以，除非，否则由式（7.1.5a）~（7.1.5d）只能得到零解。

因此对于TEM波有

（7.1.6）

从而可得到波导中的TEM波的传播特性：

传播常数

相速度

（7.1.7）

波阻抗

（7.1.7）

电场与磁场的关系

（7.1.8）

从以上的分析可知，导波系统中的TEM波的传播特性与无界空间中的均匀平面波的传播特性相同。

另外，单导体波导不能支持TEM波。

这是因为假如在波导内存在TEM波，由于磁场只有横向分量，则磁力线应在横向平面内闭合，这时就要求在波导内存在纵向的传导电流或位移电流。

但是，因为是单导体波导，其内没有纵向传导电流。

又因为TEM波的纵向电场，所以也没有纵向的位移电流。

7.1.2TM波和TE波

1.横磁波（TM波）

在传播方向上没有磁场分量，即。

故由式（7.1.5a）~（7.1.5d）得到TM波的纵向场分量与横向场分量关系

（7.1.9a）

（7.1.9b）

（7.1.9c）

（7.1.9d）

同样可以定义TM波的波阻抗，并由式（7.1.9a）~（7.1.9d）得

（7.1.10）

TM波电场和磁场关系为

（7.1.11）

2.横电波（TE波）

在传播方向上没有磁电分量，即。

故由式（7.1.5a）~（7.1.5d）得TE波的纵向场分量与横向场分量关系

（7.1.12a）

（7.1.12b）

（7.1.12c）

（7.1.12d）

TE波的波阻抗

（7.1.13）

TE波电场和磁场的关系为

（7.1.14）

对于TM波和TE波，因为或，所以，因此TM波和TE的传播常数

（7.1.15）

式中称为截止波数，其值由波导的形状、大小和传播的波型决定。

而传播常数的值决定了TM波和TE波的传播特性。

金属空芯波导内可以存在TM波和TE波，它们的传播特性由传播常数的取值范围确定，由式（7.1.15）可知，的取值范围由截止波数决定。

不同形状、不同大小的波导其截止波数的表示不同，而同一个波导中，如果传播的波的类型不同，其截止波数也不同，我们将在后面具体波导的分析中进一步讨论这个问题。

7.2矩形波导

图7.2.1矩形波导

a

b

图7.2.1所示矩形波导，宽边尺寸为a，窄边尺寸为b。

波导内填充电参数为、的理想介质，波导壁为理想导体。

由于矩形波导是单导体波导，故不能传输TEM波。

下面讨论矩形波导中TM波和TE波场分布以及它们的在波导中的传播特性。

7.2.1矩形波导中的场分布

1．矩形波导中TM波的场分布

对于TM波，因为，由式（7.1.9a）~（7.1.9d）可知，波导内的电磁场量由确定。

在给定的矩形波导中，满足下面的波动方程和边界条件：

（7.2.1）

由均匀导波系统的假设，

（7.2.2）

将其代入式（7.2.1），得

（7.2.3）

其中，称为截止波数。

该方程可利用分离变量法求解。

设其解为：

（7..2.4）

将式（7.2.4）代入式（7.2.3），然后等式两边同除以，得

（7.2.5）

式（7..2.5）中左边仅为x的函数，等式右边仅为y的函数，要使其相等，必须各等于常数。

于是，由（7.2.5）可分离出两个常微分方程

（7.2.6a）

（7.2.6b）

且

（7.2.7）

式（7.2.6）的通解为

（7.2.8）

对于图7-3所示的矩形波导，由于在x=0和x=a的边界上，满足

，（7.2.9）

于是将式（7.2.9）代入式（7.2.8）得

（7.2.10）

（7.2.11）

同理得式（7.2.6b）的通解

（7.2.12）

由边界条件

，（7.2.13）

于是得

（7.2.14）

（7.2.15）

所以，得到矩形波导中TM波的纵向场分量

（7.2.16）

式中E0=AC由激励源强度决定。

由式（7.2.7）得截止波数

（7.2.17）

利用式（7.1.9a）~（7.1.9d）可求得TM的其他横向场分量

（7.2.18a）

（7.2.18b）

（7.2.18c）

（7.2.18d）

2．矩形波导中TE波的场分布

对于TE波，波导内的电磁场量由确定，在给定的矩形波导中，满足下面的波动方程和边界条件：

（7.2.19）

仿照前面对TM的讨论，可以得到TE波的纵向场分量

（7.2.20）

式中H0=CD由激励源强度决定

截止波数

（7.2.21）

利用式（7.1.12a）~（7.1.12d）可求得TE的其他横向场分量

（7.2.22a）

（7.2.22b）

（7.2.22c）

（7.2.22d）

对于矩形波导中的TM波和TE波有下面的结论：

（1）m和n有不同的取值，对应于m、n的每一种组合即为一种可能的传播模式：

TMmn或TEmn，称为TMmn模或TEmn模；

（2）不同的模式对应不同的截止波数；

（3）由于相同的m、n组合，TMmn模和TEmn模的截止波数相同，这种情况称为模式的简并。

（4）对于TEmn其m和n可以为0（但不能同时为0），而对于TMmn模其m和n都不能为0，故不存TM0n和TMm0模。

7.2.2矩形波导中波的传播特性

矩形波导中的TM和TE波的场量均可表示为

（7.2.23）

其中

（7.2.24）

称为传播常数，矩形波导中TM波和TE波的传播特性与其取值范围有关。

（1）当传播常数为实数，即时，式（7.2.23）表示衰减的场分布。

矩形波导中不能传播相应模式的波。

此时

（7.2.25）

相应的相位常数、波导波长不存在，而波阻抗、为纯虚数。

（2）当传播常数为虚数，即，式（7.2.23）表示沿正z方向传播的波。

（7.2.26）

由此可得相位常数

（7.2.27）

波导波长（波导中相位变化时波传播的距离）

（7.2.28）

相速度

（7.2.29）

波阻抗

（7.2.30）

（7.2.31）

（3）当传播常数为零，即，这是临界情况，矩形波导中也不能传播相应模式的波。

（7.2.32）

则

即波数与截止波数相等，令

（7.2.33）

称为截止角频率。

相应的截止频率为

（7.2.34）

截止波长为

（7.2.35）

由以上讨论可得出结论：

当工作频率大于截止频率，即，波导中可以传播相应TMmn模和TEmn模式的电磁波；

当工作频率小于或等于截止频率，即，波导中不能传播相应TMmn模和TEmn模式的电磁波。

将引入的截止频率代入式（7.2.26）~（7.2.31）可把相应的传播特性参数用截止频率表示：

（7.2.36）

相位常数

（7.2.37）

波导波长

（7.2.38）

式中为无界空间中的波长。

（7.2.39）

式中为无界空间中的相速度。

（7.2.40）

（7.2.41）

例7.2.1

（1）写出边长为a和b的矩形波导中TM11模场量的瞬时表达式；

（2）求其截止频率、波导波长、相速度及波阻抗；

（3）画出xy平面和yz平面的电力线和磁力线。

解：

（1）将式（7.2.16）和式（7.2.18a）~（8.2.18d）的复数表示乘以，然后取其实部，并令m=n=1可得TM11模的瞬时场表示

（7.2.42a）

（7.2.42b）

（7.2.42c）

（7.2.42d）

（7.2.42e）

（7.2.42f）

（2）截止波长

截止频率

（3）场图

O

图7.2.2矩形波导中TM11模的场线

例7.2.2在尺寸为的矩形波导中，传输模，工作频率。

（1）求截止波长、波导波长和波阻抗。

（2）若波导的宽边尺寸增大一倍，上述参数如何变化？

还能传输什么模式？

（3）若波导的窄边尺寸增大一倍，上述参数如何变化？

解截止波长、波导波长和波阻抗可由相应的公式直接求解。

当波导尺寸发生变化，相应模式的截止波长（截止频率）将发生变化