 同步培优人教版 九年级数学上册 二次函数图像性质 培优练习含答案Word文档格式.docx
同步培优人教版 九年级数学上册 二次函数图像性质 培优练习含答案Word文档格式.docx
- 文档编号:14338221
- 上传时间:2022-10-22
- 格式:DOCX
- 页数:10
- 大小:457.97KB
同步培优人教版 九年级数学上册 二次函数图像性质 培优练习含答案Word文档格式.docx
《同步培优人教版 九年级数学上册 二次函数图像性质 培优练习含答案Word文档格式.docx》由会员分享,可在线阅读,更多相关《同步培优人教版 九年级数学上册 二次函数图像性质 培优练习含答案Word文档格式.docx(10页珍藏版)》请在冰豆网上搜索。
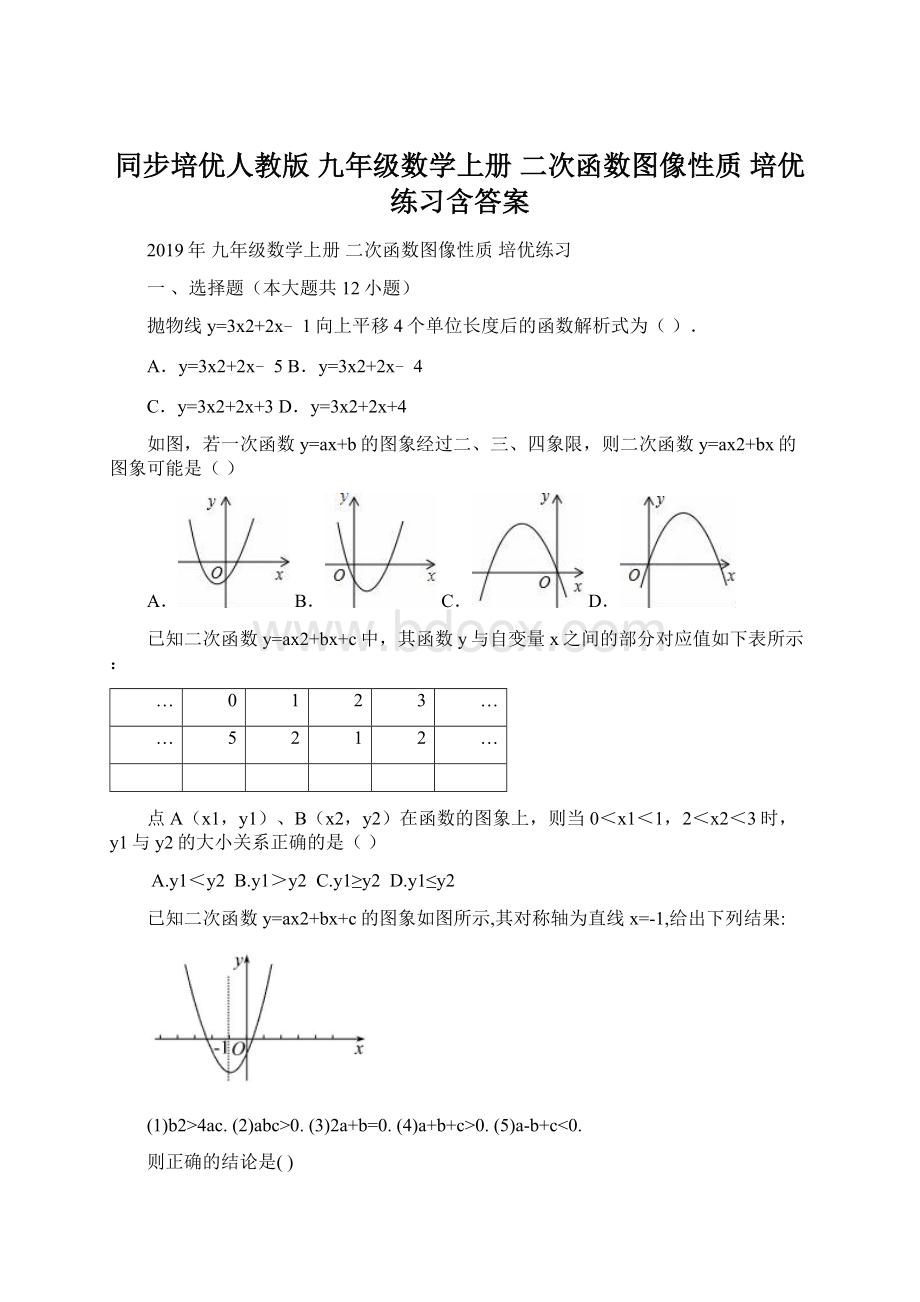
点A(x1,y1)、B(x2,y2)在函数的图象上,则当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是()
A.y1<y2B.y1>y2C.y1≥y2D.y1≤y2
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结果:
(1)b2>
4ac.
(2)abc>
0.(3)2a+b=0.(4)a+b+c>
0.(5)a-b+c<
0.
则正确的结论是()
A.
(1)
(2)(3)(4)B.
(2)(4)(5)C.
(2)(3)(4)D.
(1)(4)(5)
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;
②2a﹣b<0;
③a+c<1;
④b2+8a>4ac.其中正确的有()
A.1个B.2个C.3个D.4个
在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是()
设a、b是常数,且b>0,抛物线y=ax2+bx+a2﹣5a﹣6为下图中四个图象之一,则a的值为()
A.6或﹣1B.﹣6或1C.6D.﹣1
如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:
s),四边形PBDQ的面积为y(单位:
cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为()
A.B.C.D.
如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0;
②a﹣2b+4c=0;
③25a﹣10b+4c=0;
④3b+2c>0;
⑤a﹣b≥m(am-b).
其中所有正确的结论是()
A.①②③B.①③④C.①②③⑤D.①③⑤
如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°
,点B在抛物线y=ax2(a<0)的图象上,则a的值为()
A.B.C.﹣2D.
如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;
过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是()
如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是()
二、填空题(本大题共6小题)
把抛物线y=ax2+bx+c的图象先向右平移3个单位长度,再向下平移2个单位长度,所得图象的解析式是y=x2-3x+5,则a+b+c=.
如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°
,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为.
如图所示,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过正方形ABOC的三顶点A,B,C,则ac的值是.
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:
①abc<0;
②a+b=0;
③4ac-b2=4a;
④a+b+c<0.其中正确的有____个。
如图,抛物线y=﹣x2+bx+c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为.
已知实数m,n满足m﹣n2=1,则代数式m2+2n2+4m﹣1的最小值等于
.
三、解答题(本大题共6小题)
如图,抛物线y=x2+bx+c过点A(-4,-3),与y轴交于点B,对称轴是x=-3,请回答下列问题:
(1)求抛物线的解析式.
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.
如图,二次函数y=ax2-4x+c的图象过原点,与x轴交于点A(-4,0).
(1)求此二次函数的解析式.
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
已知二次函数y=ax2-4x+c的图象过点(-1,0)和点(2,-9).
(1)求该二次函数的解析式并写出其对称轴;
(2)已知点P(2,-2),连结OP,在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).
如图,四边形ABCO为矩形,点A在x轴上,点C在y轴上,且点B的坐标为(﹣1,2),将此矩形绕点O顺时针旋转90°
得矩形DEFO,抛物线y=﹣x2+bx+c过B,E两点.
(1)求此抛物线的函数关系式.
(2)将矩形ABCO向左平移,并且使此矩形的中心在此抛物线上,求平移距离.
(3)将矩形DEFO向上平移距离d,并且使此抛物线的顶点在此矩形的边上,则d的值是.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在
(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
参考答案
C
B
D
A
答案:
11
答案为:
P(,2).
答案为:
-2
3个;
4;
(1)∵对称轴是x=-=-3,a=1,∴b=6.
又∵抛物线y=x2+bx+c过点A(-4,-3),∴(-4)2+6×
(-4)+c=-3,解得c=5.
∴抛物线的解析式为y=x2+6x+5.
(2)∵和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,
∴点C的横坐标为-7,∴点C的纵坐标为y=(-7)2+6×
(-7)+5=12.
又∵抛物线的解析式为y=x2+6x+5与y轴交于点B(0,5),
∴CD边上的高为12-5=7,∴△BCD的面积为×
8×
7=28.
解:
(1)依题意,得解得
∴二次函数的解析式为y=-x2-4x.
(2)令P(m,n),则S△AOP=AO·
|n|=×
4|n|=8,解得n=±
4,
又∵点P(m,n)在抛物线y=-x2-4x上,
∴-m2-4m=±
4,分别解得m1=-2,m2=-2+2和m3=-2-2,
∴P1(-2,4),P2(-2+2,-4),P3(-2-2,-4).
(1)
对称轴是x=2
(2)
⑴设抛物线的解析式为y
=ax2+bx+c,则有:
解得:
所以抛物线的解析式为y
=x2-2x-3.
⑵令x2-2x-3=0,解得x1=-1,x2=3,所以B点坐标为(3,0).
设直线BC的解析式为y
=kx+b,则,解得,所以直线解析式是y
=x-3.
当x=1时,y=-2.所以M点的坐标为(1,-2)
(1)∵二次函数y=x2+mx+2m﹣7的图象经过点(1,0),
∴1+m+2m﹣7=0,解得m=2.∴抛物线的表达式为y=x2+2x﹣3;
(2)y=x2+2x﹣3=(x+1)2﹣4.
∵当﹣4<x<﹣1时,y随x增大而减小;
当﹣1≤x<1时,y随x增大而增大,∴当x=﹣1,y最小=﹣4.
当x=﹣4时,y=5.∴﹣4<x<1时,y的取值范围是﹣4≤y<5;
(3)y=x2+2x﹣3与x轴交于点(﹣3,0),(1,0).新图象M如右图红色部分.
把抛物线y=x2+2x﹣3=(x+1)2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),
当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<.
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 同步培优人教版 九年级数学上册 二次函数图像性质 培优练习含答案 同步 培优人教版 九年级 数学 上册 二次 函数 图像 性质 练习 答案
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 转基因粮食的危害资料摘编Word下载.docx
转基因粮食的危害资料摘编Word下载.docx
