钢管订购和运输数学建模Word格式.docx

钢管订购和运输数学建模Word格式.docx

《钢管订购和运输数学建模Word格式.docx》由会员分享，可在线阅读，更多相关《钢管订购和运输数学建模Word格式.docx（16页珍藏版）》请在冰豆网上搜索。

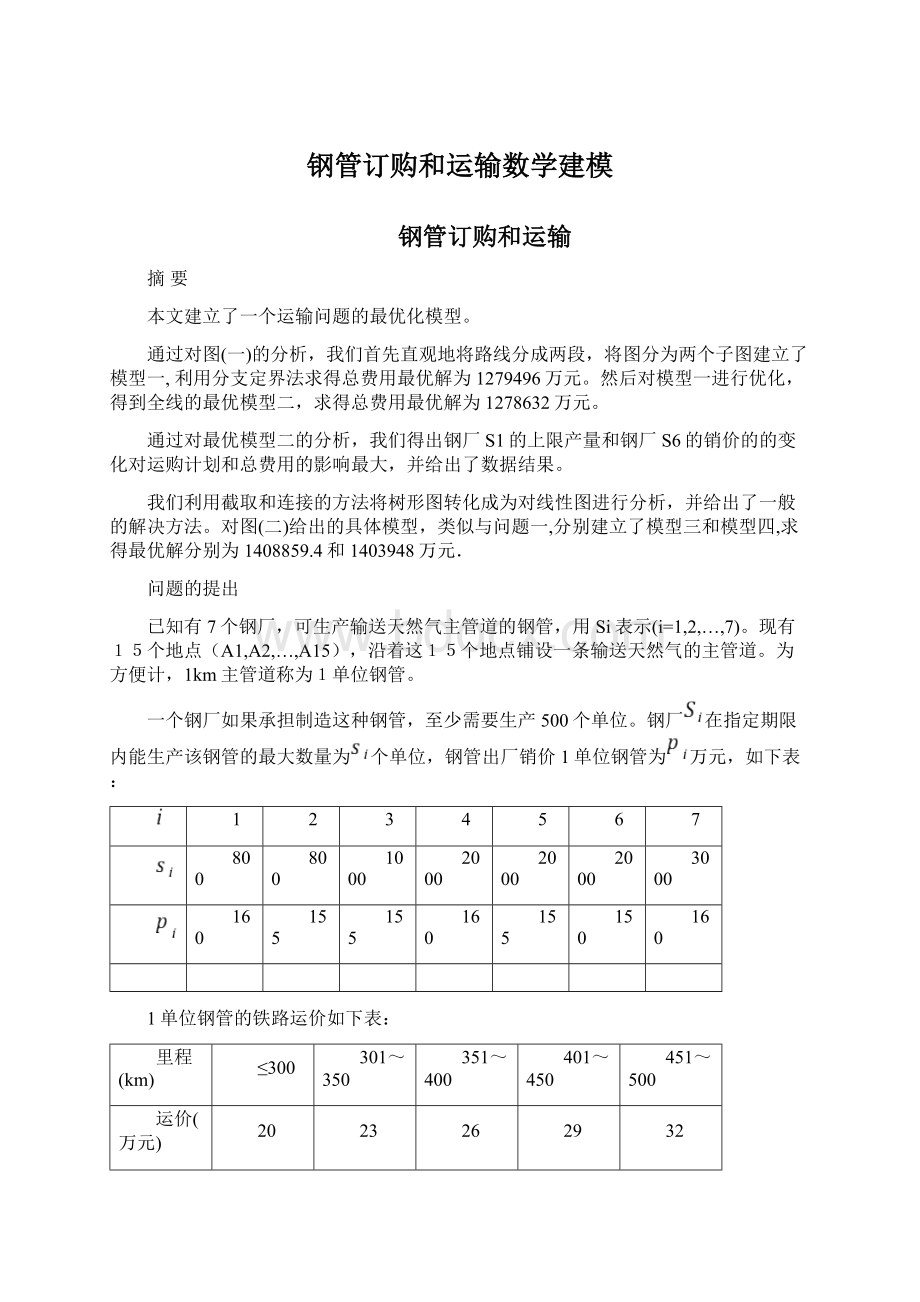
≤300

301～350

351～400

401～450

451～500

运价（万元）

20

23

26

29

32

501～600

601～700

701～800

801～900

901～1000

37

44

50

55

60

1000km以上每增加1至100km运价增加5万元。

公路运输费用为1单位钢管每公里0.1万元（不足整公里部分按整公里计算）。

钢管可由铁路、公路运往铺设地点（不只是运到点，而是管道全线）。

（1）请制定一个主管道钢管的订购和运输计划，使总费用最小（给出总费用）。

（2）请就

（1）的模型分析：

哪个钢厂钢管的销价的变化对购运计划和总费用影响最大，哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大，并给出相应的数字结果。

（3）如果要铺设的管道不是一条线，而是一个树形图，铁路、公路和管道构成网络，请就这种更一般的情形给出一种解决办法，并对图二按

（1）的要求给出模型和结果。

二、问题的分析

该问题是图论中运输问题的最优化问题。

经过分析，我们认为总费用可分为两种费用进行求解，分别为：

（1）销价和运输钢管至管道结点Ai（i=1,2,…,15）的总费用（称为成本费用）

（2）铺设过程中的运输费用；

要解决此问题，我们认为有两点关键：

（1）如何求出Ai（i=1,2,…,15）至Si（i=1,2,…,7）的最小成本费用；

（2）如何调整使得各路径满足题中的最优指标。

针对上述问题，我们分别运用了图上作业法、枚举法、逐次修正法、重绕最小生成树法等方法，在综合考虑算法的精度和算法的复杂度后，我们选择了图上作业法、枚举法、逐次修正法对模型进行逐次优化，直至求得最优解。

三、模型的基本假设及符号说明

（一）基本假设：

（1）运输方式的改变所花费用包含在运费中；

（2）铁路线上任意两点可以直达，不需中途转车，即铁路线上两点

间运费按线路总长计算；

（3）假设一单位钢管可由任意长度钢管组成，购买钢管可以非整数单位购买;

（4）不考虑其它外界因素对费用的影响；

（5）钢管在铺设时，先将钢管运到结点处，再由结点处向左右两方相邻结点铺设；

（6）在Si厂购买钢管要么为零,要么至少为500单位。

（二）符号说明：

xij：

从钢厂Si运到结点Aj的单位钢管数；

fij：

单位钢管从钢厂Si运到结点Aj的的最少成本费用；

tj：

第Aj点与Aj+1点间的路线长度，j=1,2,…,14；

yj：

从结点Aj开始沿管道向右铺设的路线长度,j=1,2,3,…,15；

w：

钢管订购和运输的总费用；

mi:

钢厂Si的最小产量，mi=500，i=1,2,3,4,5,6,7

ni:

钢厂Si的产量上限，ni=si，i=1,2,…，7

bi:

图一中各节点（见附录七）

Vi:

图二中各节点（见附录八）

四、模型的建立与求解

（一）问题一及其求解：

针对图

（一），我们首先采用图上作业法对所给图进行分析，利用枚举法，我们求出一单位钢管由钢管厂Si运输至管道结点Ａi的最小成本费用，具体数据如下表：

表一单位钢管由Si运输至Ａi的最小成本费用

（单位：

万元）

S1

S2

S3

S4

S5

S6

S7

A1

330.7

370.7

385.7

420.7

410.7

415.7

435.7

A2

320.3

360.3

375.3

410.3

400.3

405.3

425.3

A3

300.2

345.2

355.2

395.2

380.2

385.2

405.2

A4

258.6

326.6

336.6

376.6

361.6

366.6

386.6

A5

198

266

276

316

301

306

326

A6

180.5

250.5

260.5

300.5

285.5

290.5

310.5

A7

163.1

241

251

291

281

A8

181.2

226.2

241.2

276.2

266.2

271.2

291.2

A9

224.2

269.2

203.2

244.2

234.2

259.2

A10

252

297

237

222

212

A11

256

211

188

201

226

A12

311

221

206

195

216

A13

281.2

326.2

236.2

176.2

198.2

A14

288

333

273

243

228

161

186

A15

302

347

287

257

242

178

162

这样，原问题即转化为通常的运输问题。

我们进一步对上表数据进行分析，得到结论：

结论1：

将Ｓ4、S5两列数据进行对比，发现同一行中S4列数据均大于S5列。

由此得出，应优先考虑钢厂S5，只有当对S5的需求量超过其最大产量时，才需要考虑钢厂S4。

进一步对原图进行分析可得：

结论2：

由于A1点只有通过A2点才能与钢厂Si连接,故模型中不需考虑往A1运输钢管。

模型

（一）：

对表一数据进一步分析。

将各行数据由小到大排序，发现由A2至A9各行中费用最小的前四个数据均在S1,S2,S3,S5列中，由A10至A15各行中费用最小的前三个数据均在S5,S6,S7中，直观感觉到：

A1至A9需要来自S6及S7等后一部分钢厂的钢管的可能性很小，而且A9至A15不太可能需要S1、S2、S3等前一部分钢厂生厂的钢管，故把原图分为两个子图考虑，分别为A1至A9和A9至A15，即分为两个子模型，分别进行最优化，得到两个子模型（非线性规划模型）如下：

子模型1：

子模型2：

由于这两个子模型属于非线性规划问题，且第一个约束条件很复杂，利用结论1、2，采用分支定界法用LINGO软件分别进行编程（见附录一、二）得到：

w1=859629.3w2=419866.7

模型一的总费用为w=w1+w2=1279496（万元）。

模型

（二）：

由于前面的模型直观将管道分为两端，即原图分为两个子图，可能存在一定的误差。

下面对模型

（一）进行优化，即对主管道建立统一模型，如下：

同样利用结论1、2并采用分支定界法，利用LINGO软件编程（见附录三）运行得出

:

最优解W=1278632万元，各节点向右铺设的管道单位数：

Y1=0Y2=175Y3=282Y4=0Y5=10

Y6=16Y7=76Y8=175Y9=159Y10=30

Y11=145Y12=11Y13=34Y14=335

表二各钢厂定购计划：

数量

1237.5

1333.5

表三运输计划如下（bi含义参见附图七）:

路线运量

S1-b7-b6-b5-A5-A4;

335

S1-b7-b6-A6;

200

S1-A7;

265;

S2-b8-b4-b2-b1-A2;

179

S2-b8-b4-b2-b3-A3;

131.3

S2-b8-S1-b7-b6-b5-A5-A4;

116

S2-b8-S1-b7-b6-b5-A5;

73.7

S2-b8-A8;

300

S3-b9-b8-b4-b2-b3-A3;

319

S3-b9-b8-S1-b7-b6-b5-A5-A4;

11

S3-b9-A9;

604

S5-b12-b11-b10-b9-b8-b4-b2-b3-A3;

57.7

S5-b12-b11-b10-b9-b8-S1-b7-b6-b5-A5;

542.3

S5-b12-b11-b10-A10;

222.5

S5-b12-A11;

415

S6-b16-b15-b13-b11-b10-A10;

128.8

S6-b16-b15-b13-b14-A12;

86

S6-b16-b15-A13;

333

S6-A14;

621

S6-b16-b17-A15;

165

（二）问题

（2）的求解

通过模型

（二）的求解，我们确定对图

（一）仅需要S1、S2、S3、S5、S6承担生产任务即可取得最优解。

对模型所用程序进行灵敏度分析，并具体考虑当钢厂钢管的销价增加1万元或产量上限增加1单位时，购运计划和总费用的变化情况，结果如下表：

表四钢厂Si的钢管产量上限增加1单位对总费用的影响

总费用

1278529

1278597

1278607

1278632

减少量

103

35

25

则可以发现：

钢厂S1的钢管产量上限的变动对购运计划和总费用影响最大。

表五钢厂Si的钢管销价增加1万元对总费用的影响

1279432

1279632

1279639

1379834

增加量

1007

1202

钢厂S6的钢管销价的微小变动对购运计划和总费用影响最大。

（三）问题（3）的求解

1、一般模型

经过对图

（一）的分析求解可以看出，订购及运输钢管的总费用可由各段所需费用求和得到。

若要铺设的管道是一个树形图，则可以将其转化为线性管道进行分析。

具体解题步骤如下：

（1）运用图论的最小权匹配法（简单图可利用枚举法），求出从各钢厂定购并运输一单位钢管