正弦定理和余弦定理Word文档格式.docx

正弦定理和余弦定理Word文档格式.docx

《正弦定理和余弦定理Word文档格式.docx》由会员分享，可在线阅读，更多相关《正弦定理和余弦定理Word文档格式.docx（13页珍藏版）》请在冰豆网上搜索。

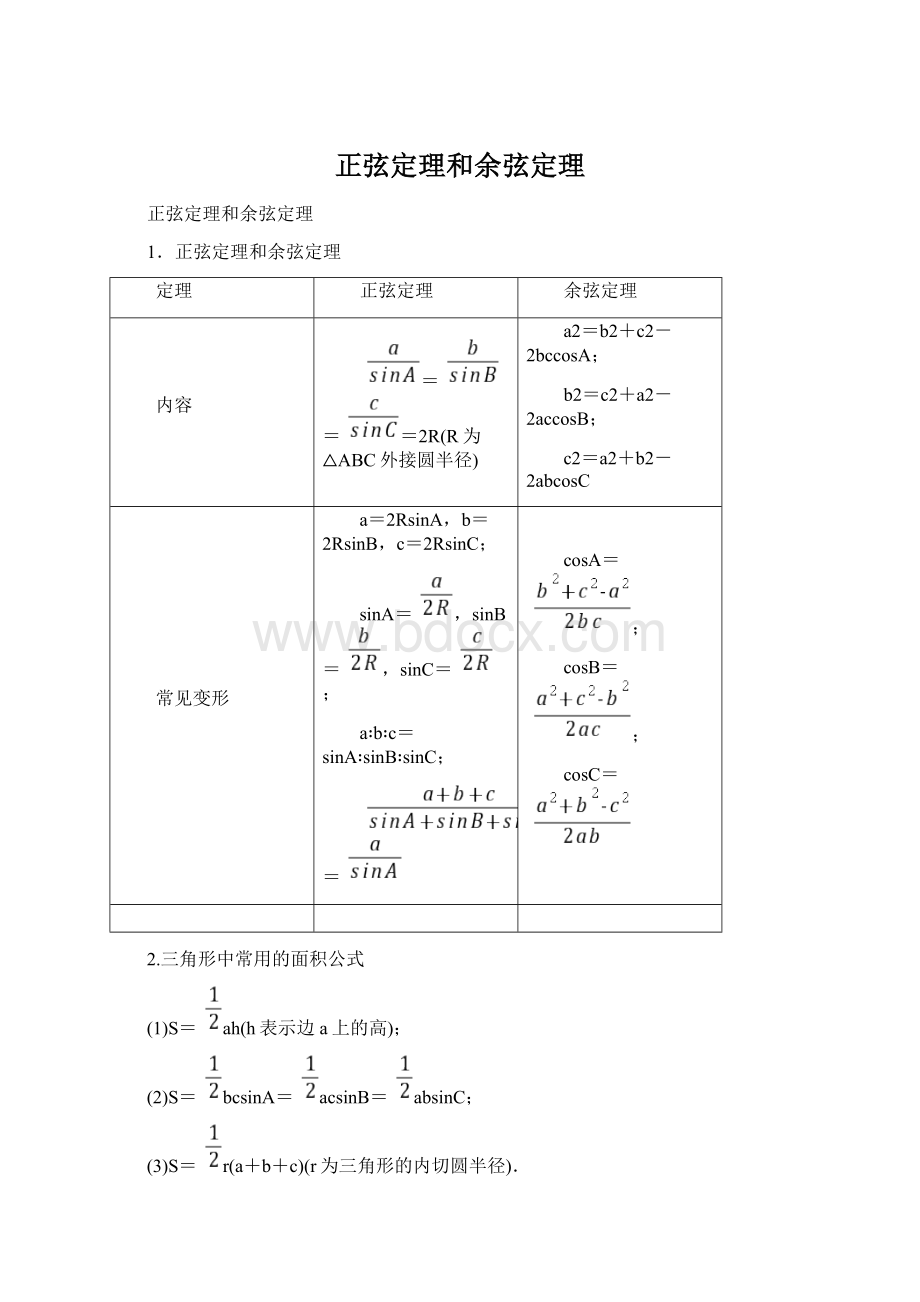
A为锐角

A为钝角或直角

图形

关系式

a＝bsinA

bsinA<

a<

b

a≥b

a>

解的个数

一解

两解

|微点提醒|

1．三角形中的三角函数关系

（1）sin（A＋B）＝sinC；

（2）cos（A＋B）＝－cosC；

（3）sin＝cos；

（4）cos＝sin.

2．三角形中的射影定理

在△ABC中，a＝bcosC＋ccosB；

b＝acosC＋ccosA；

c＝bcosA＋acosB.

3．利用正、余弦定理解三角形时，要注意三角形内角和定理对角的范围的限制．

‖易错辨析‖

判断下列结论是否正确（请在括号中打”√”或“×

”）

（1）在△ABC中，已知a，b和角B，能用正弦定理求角A；

已知a，b和角C，能用余弦定理求边c.（√）

（2）在三角形中，已知两角和一边或已知两边和一角都能解三角形．（√）

（3）在△ABC中，sinA>

sinB的充分不必要条件是A>

B.（×

）

（4）在△ABC中，“a2＋b2<

c2”是“△ABC为钝角三角形”的充分不必要条件．（√）

（5）在△ABC的角A，B，C，边长a，b，c中，已知任意三个可求其他三个．（×

‖自主测评‖

1．（教材改编题）在△ABC中，已知a＝5，b＝7，c＝8，则A＋C＝（　　）

A．90°

B．120°

C．135°

D．150°

解析：

选B　cosB＝＝＝.

所以B＝60°

，所以A＋C＝120°

.

2．（教材改编题）在非钝角△ABC中，2bsinA＝a，则角B为（　　）

A.B.

C.D.

选C　由正弦定理得bsinA＝asinB，

所以2asinB＝a，即sinB＝，又B为非钝角，所以B＝，故选C.

3．在△ABC中，若a＝18，b＝24，A＝45°

，则此三角形（　　）

A．无解B．有两解

C．有一解D．解的个数不确定

选B　因为＝，

所以sinB＝·

sinA＝×

sin45°

＝.

又因为a<

b，所以B有两解.

4．（教材改编题）已知△ABC的三边之比为3∶5∶7，则最大角为（　　）

选A　由三边之比为a∶b∶c＝3∶5∶7，可设a＝3k，b＝5k，c＝7k（k>

0），由余弦定理得cosC＝＝＝－，又0<

C<

π，所以C＝.

5．在△ABC中，角A，B，C所对的边分别为a，b，c，cos2A＝sinA，bc＝2，则△ABC的面积为________．

由cos2A＝sinA，得1－2sin2A＝sinA，解得sinA＝（负值舍去），由bc＝2，可得△ABC的面积S＝bcsinA＝×

2×

答案：

………………考点一　利用正、余弦定理解三角形……|多维探究型|……………

|多角探明|

角度一　求三角形的边长

【例1】　（2018届贵阳模拟）在△ABC中，内角A，B，C的对边a，b，c成公差为2的等差数列，C＝120°

（1）求边长a；

（2）（一题多解）求AB边上的高CD的长．

[解]　

（1）由题意得b＝a＋2，c＝a＋4，

由余弦定理cosC＝得cos120°

＝，即a2－a－6＝0，∴a＝3或a＝－2（舍去），∴a＝3.

（2）解法一：

由

（1）知a＝3，b＝5，c＝7，由三角形的面积公式得absin∠ACB＝c×

CD，∴CD＝＝＝，即AB边上的高CD＝.

解法二：

由

（1）知a＝3，b＝5，c＝7，

由正弦定理得＝＝，

即sinA＝，

在Rt△ACD中，CD＝ACsinA＝5×

＝，

即AB边上的高CD＝.

角度二　求三角形的角或角的三角函数值

【例2】　

（1）在△ABC中，B＝，BC边上的高等于BC，则cosA＝（　　）

A.B.

C．－D．－

（2）（2018届河北“五个一名校联盟”模拟）已知a，b，c分别是△ABC的内角A，B，C所对的边，且c＝2，C＝，若sinC＋sin（B－A）＝2sin2A，则A＝________.

[解析]　

（1）设△ABC中角A，B，C的对边分别是a，b，c，由题意可得a＝csin＝c，则a＝c.在△ABC中，由余弦定理可得b2＝a2＋c2－ac＝c2＋c2－3c2＝c2，则b＝c.由余弦定理，可得cosA＝＝＝－，故选C.

（2）在△ABC中，由sinC＋sin（B－A）＝2sin2A可得sin（A＋B）＋sin（B－A）＝2sin2A，即sinAcosB＋cosAsinB＋cosAsinB－sinAcosB＝4sinAcosA，∴cosAsinB＝2sinAcosA，即cosA（sinB－2sinA）＝0，即cosA＝0或sinB＝2sinA，

①当cosA＝0时，A＝；

②当sinB＝2sinA时，根据正弦定理得b＝2a，

由余弦定理c2＝b2＋a2－2abcosC，结合c＝2，C＝，得a2＋b2－ab＝4，

∴a＝，b＝，∴b2＝a2＋c2，∴B＝，∴A＝.

综上可得，A＝或.

[答案]　

（1）C　

（2）或

『名师点津』………………………………………………|品名师指点迷津|

应用正弦、余弦定理的解题技巧

（1）求边：

利用公式a＝，b＝，c＝或其他相应变形公式求解．

（2）求角：

先求出正弦值，再求角，即利用公式sinA＝，sinB＝，sinC＝或其他相应变形公式求解．

（3）已知两边和夹角或已知三边可利用余弦定理求解．

（4）灵活利用式子的特点转化；

如出现a2＋b2－c2＝λab形式用余弦定理，等式两边是关于边或角的正弦的齐次式用正弦定理．

|变式训练|

1．（2018届福建莆田联考）在△ABC中，内角A，B，C的对边分别为a，b，c，若asinBcosC＋csinBcosA＝b，且a>

b，则B＝（　　）

选A　∵asinBcosC＋csinBcosA＝b，∴根据正弦定理可得sinAsinBcosC＋sinCsinBcosA＝sinB，即sinB（sinAcosC＋sinCcosA）＝sinB.∵sinB≠0，∴sin（A＋C）＝，即sinB＝.∵a>

b，∴A>

B，即B为锐角，∴B＝，故选A.

2．（2019届黄冈模拟）在△ABC中，角A，B，C的对边分别为a，b，c.

（1）若23cos2A＋cos2A＝0，且△ABC为锐角三角形，a＝7，c＝6，求b的值；

（2）若a＝，A＝，求b＋c的取值范围．

解：

（1）∵23cos2A＋cos2A＝23cos2A＋2cos2A－1＝0，

∴cos2A＝，

又A为锐角，∴cosA＝，

a2＝b2＋c2－2bccosA，即b2－b－13＝0，

得b＝5（负值舍去），∴b＝5.

由正弦定理可得b＋c＝2（sinB＋sinC）＝2＝2sin，

又0<

B<

，∴<

B＋<

sin≤1，∴b＋c∈（，2]．

由余弦定理a2＝b2＋c2－2bccosA可得b2＋c2－3＝bc，

∴（b＋c）2－3＝3bc≤（b＋c）2，当且仅当b＝c时取等号，

∴b＋c≤2，又由两边之和大于第三边可得b＋c>

，

∴b＋c∈（，2]．

………………考点二　判断三角形的形状…………|重点保分型|……………

|研透典例|

【典例】　（一题多解）在△ABC中，若a2＋b2－c2＝ab，且2cosAsinB＝sinC，试判断△ABC的形状．

[解]　解法一：

利用边的关系来判断

由正弦定理得＝，

由2cosAsinB＝sinC，有cosA＝＝.

又由余弦定理得cosA＝，

所以＝，

即c2＝b2＋c2－a2，所以a2＝b2，所以a＝b.

又因为a2＋b2－c2＝ab.

所以2b2－c2＝b2，所以b2＝c2，

所以b＝c，所以a＝b＝c.

所以△ABC为等边三角形．

利用角的关系来判断

因为A＋B＋C＝180°

所以sinC＝sin（A＋B），

又因为2cosAsinB＝sinC，

所以2cosAsinB＝sinAcosB＋cosAsinB，

所以sin（A－B）＝0.

又因为A与B均为△ABC的内角，所以A＝B，

又由a2＋b2－c2＝ab，

由余弦定理，得cosC＝＝＝，

又0°

<

180°

所以C＝60°

所以△ABC为等边三角形.

判定三角形形状的两种常用途径

[提醒]“角化边”后要注意用因式分解、配方等方法得出边的相应关系；

“边化角”后要注意用三角恒等变换公式、三角形内角和定理及诱导公式推出角的关系．

在△ABC中，若（a2＋b2）sin（A－B）＝（a2－b2）sin（A＋B），则△ABC的形状是（　　）

A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰三角形或直角三角形

选D　因为（a2＋b2）sin（A－B）＝（a2－b2）sin（A＋B），所以b2[sin（A＋B）＋sin（A－B）]＝a2[sin（A＋B）－sin（A－B）]，

所以2sinAcosB·

b2＝2cosAsinB·

a2，

即a2cosAsinB＝b2sinAcosB.

解法一：

由正弦定理知a＝2RsinA，b＝2RsinB，

所以sin2AcosAsinB＝sin2BsinAcosB，

又sinA·

sinB≠0，

所以sinAcosA＝sinBcosB，所以sin2A＝sin2B.

在△ABC中，0<

2A<

2π，0<

2B<

2π，

所以2A＝2B或2A＝π－2B.所以A＝B或A＋B＝.

所以△ABC为等腰三角形或直角三角形，故选D.

由正弦定理、余弦定理得：

a2b＝b2a，

所以a2（b2＋c2－a2）＝b2（a2＋c2－b2），

所以（a2－b2）（a2＋b2－c2）＝0，

所以a2－b2＝0或a2＋b2－c2＝0，

即a＝b或a2＋b2＝c2.

所以△ABC为等腰三角形或直角三角形．故选D.

………………考点三　三角形面积的计算………………|多维探究型|……………

角度一　求三角形的面积

【例1】　（2018届武汉调研）在△ABC中，a，b，c分别是角A，B，C的对边，且2bcosC＝2a＋c.

（1）求B；

（2）若b＝2，a＋c＝，求△ABC的面积．

[解]　

（1）由正弦定理，知2sinBcosC＝2sinA＋sinC，

由A＋B＋C＝π，得2sinBcosC＝2sin（B＋C）＋sinC，

化简，得2sinBcosC＝2（sinBcosC＋cosBsinC）＋sinC，

即2cosBsinC＋sinC＝0.

因为sinC≠0，所以cosB＝－.

因为0<

π，所以B＝.

（2）由余弦正理b2＝a2＋c2－2accosB，可知b2＝（a＋c）2－2ac－2accosB，

因为b＝2，a＋c＝，所以22＝（）2－2ac－2accos，得ac＝1.

所以S△ABC＝