凸轮机构设计说明书Word下载.docx

凸轮机构设计说明书Word下载.docx

《凸轮机构设计说明书Word下载.docx》由会员分享，可在线阅读，更多相关《凸轮机构设计说明书Word下载.docx（18页珍藏版）》请在冰豆网上搜索。

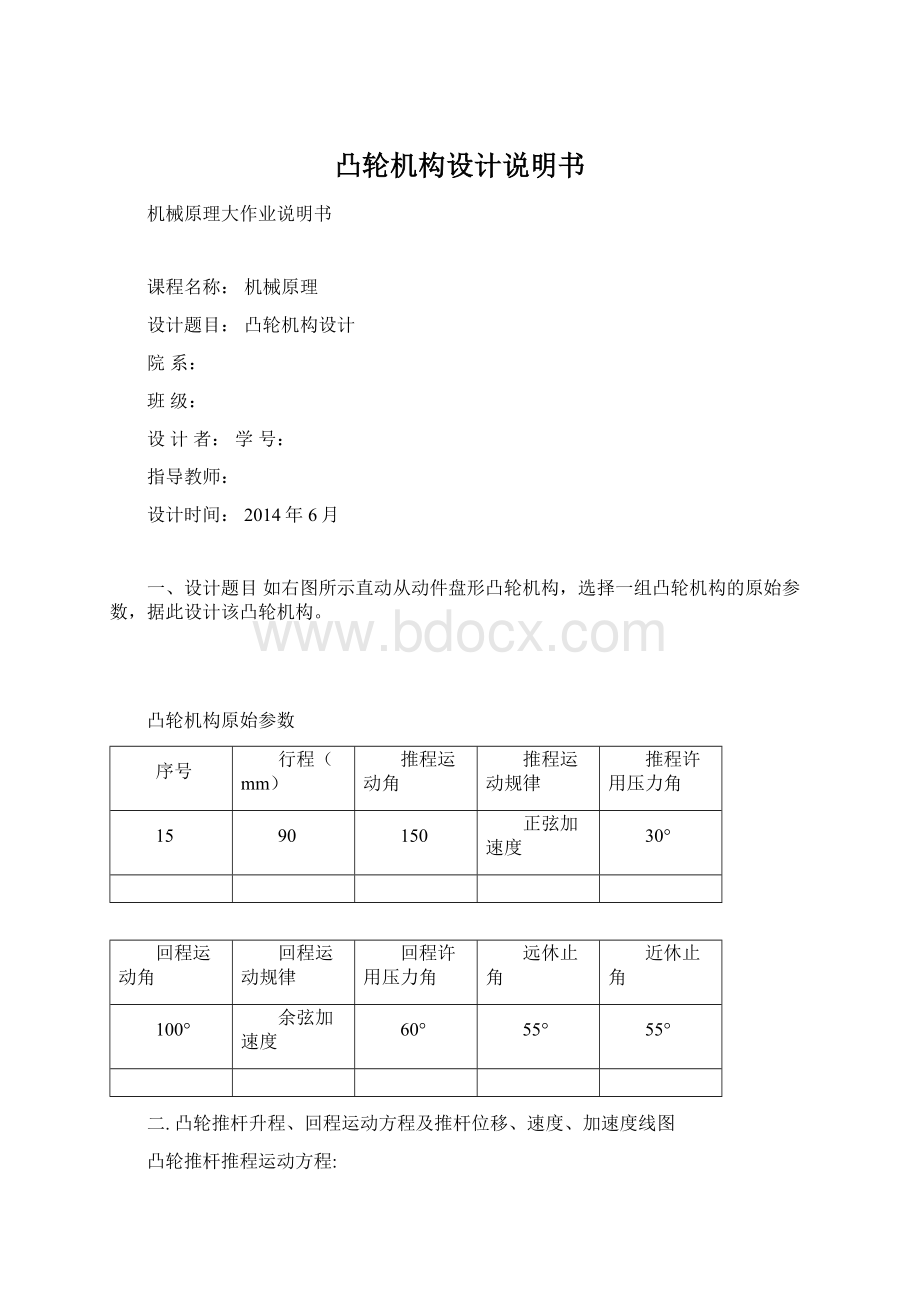
凸轮机构原始参数

序号

行程（mm）

推程运动角

推程运动规律

推程许用压力角

15

90

150

正弦加速度

30°

回程运动角

回程运动规律

回程许用压力角

远休止角

近休止角

100°

余弦加速度

60°

55°

二.凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图

凸轮推杆推程运动方程:

凸轮推杆回程运动方程

%t表示转角，s表示位移

t=0:

0.01:

5*pi/6;

%升程阶段

s=90*[（6*t）/（5*pi）-1/（2*pi）*sin（12*t/5）];

holdon

plot（t,s）;

t=5*pi/6:

41*pi/36;

%远休止阶段

s=90;

t=41*pi/36:

61*pi/36;

%回程阶段

s=45*[1+cos（（9*t/5）-（41*pi/20））];

t=61*pi/36:

2*pi;

%近休止阶段

s=0;

gridon

holdoff

%t表示转角，令ω1=1

v=108*1*[1-cos（12*t/5）]/pi

plot（t,v）;

v=0

v=-81*1*sin（（9*t/5）-（41*pi/20））

0.001:

a=259.2*sin（12*t/5）/pi;

plot（t,a）;

t=5*pi/6:

a=0;

a=-145.8*cos（（9*t/5）-（41*pi/20））;

三.绘制凸轮机构的线图

%t表示转角，x（横坐标）表示速度ds/dφ，y（纵坐标）表示位移s

%升程阶段

x=108*1*（1-cos（12*t/5））/pi;

y=90*（（6*t）/（5*pi）-1/（2*pi）*sin（12*t/5））;

plot（x,y,'

-r'

）;

x=0;

y=90;

%回程阶段

x=-81*1*sin（（9*t/5）-（41*pi/20））;

y=45*（1+cos（（9*t/5）-（41*pi/20）））;

holdon

y=0;

四.按许用压力角确定凸轮基圆半径和偏距

1.求切点转角

（1）在图-4中，右侧曲线为升程阶段的类速度-位移图，作直线Dtdt与其相切，且位移轴正方向呈夹角[1]=300,则切点处的斜率与直线Dtdt的斜率相等，因为kDtdt=tan300,右侧曲线斜率可以表示为,所以，，通过编程求其角度。

编码：

求得转角t=1.1123

进而求的切点坐标（x,y）=（93.8817,45.8243）

（2）在图-4中，左侧曲线为回程阶段的类速度-位移图，作直线D’td’t与其相切，且位移轴正方向呈夹角[1]=600,则切点处的斜率与直线D’td’t的斜率相等，因为kDtdt=tan300

同理求得切点坐标（x,y）=（-110.0654,42.3144）

2.确定直线方程

直线Dtdt：

y=tan（pi/3）（x-93.8817）=45.8243;

直线Dt’dt’:

y=-tan（pi/3）（x+84.3144）=110.0654;

3.绘图确定基圆半径和偏距

%直线Dtdt

x=-125:

1:

150;

y=tan（pi/3）*（x-93.8798）+45.8243;

plot（x,y）;

%直线Dt’dt’

y=-tan（pi/6）*（x+110.0654）+34.3144;

%直线Dd

x=0:

y=tan（2*pi/3）*x;

x=108*1*[1-cos（12*t/5）]/pi;

y=90*[（6*t）/（5*pi）-1/（2*pi）*sin（12*t/5）];

y=45*[1+cos（（9*t/5）-（41*pi/20））];

如图，在这三条直线所围成的公共许用区域，只要在公共许用区域选定凸轮轴心O的位置，凸轮基圆半径r0和偏距e就可以确定了。

现取轴心位置为x=20，y=-125，则可得偏距e=20，基圆半径

=127

五.绘制凸轮理论轮廓线

%凸轮的理论轮廓，t表示转角，x表示横坐标，y表示纵坐标

0.0001:

x=（125+130*[（6*t）/（5*pi）-1/（2*pi）*sin（12*t/5）]）.*cos（t）-20*sin（t）;

y=（125+130*[（6*t）/（5*pi）-1/（2*pi）*sin（12*t/5）]）.*sin（t）+20*cos（t）;

pi;

x=（125+130）.*cos（t）-20*sin（t）;

y=（125+130）.*sin（t）+20*cos（t）;

t=pi:

14*pi/9;

x=（125+65*[1+cos（9*（t-pi）/5）]）.*cos（t）-20*sin（t）;

y=（125+65*[1+cos（9*（t-pi）/5）]）.*sin（t）+20*cos（t）;

t=14*pi/9:

x=（125）.*cos（t）-20*sin（t）;

y=（125）.*sin（t）+20*cos（t）;

%基圆

x=20.1074*cos（t）;

y=20.1074*sin（t）;

%偏心圆

x=13.3509*cos（t）;

y=13.3509*sin（t）;

六、在理论廓线上分别绘出基圆与偏距圆：

x=127*cos（t）;

y=127*sin（t）;

x=20*cos（t）;

y=20*sin（t）;

七.确定滚子半径

1.绘制曲率半径图

%凸轮理论轮廓半径，t表示转角，p表示曲率半径,

%dxi表示dx/dφ,dyi表示dy/dφ,i=1,2,3,4

h=130;

%升程

t0=pi*5/6;

%升程角

t01=pi*5/9;

%回程角

ts=pi/6;

%远休止角

ts1=pi*4/9;

%近休止角

e=20;

%偏距

s0=125;

%升程阶段

t=linspace（0,pi*5/6,1000）;

s=h*（t/t0-sin（2*pi*t/t0）/（2*pi））;

dx1=（h/t0-h*cos（2*pi*t/t0））.*cos（t）-（s0+s）.*sin（t）-e*cos（t）;

dy1=（h/t0-h*cos（2*pi*t/t0））.*sin（t）+（s0+s）.*cos（t）-e*sin（t）;

p=sqrt（dx1.^2+dy1.^2）;

plot（t,p）;

%远休止阶段

t=linspace（pi*5/6,pi,1000）;

s=h;

dx2=-sin（t）.*（s+s0）-e*cos（t）;

dy2=cos（t）.*（s