回归分析应用实例讲解文档格式.docx

回归分析应用实例讲解文档格式.docx

《回归分析应用实例讲解文档格式.docx》由会员分享，可在线阅读，更多相关《回归分析应用实例讲解文档格式.docx（17页珍藏版）》请在冰豆网上搜索。

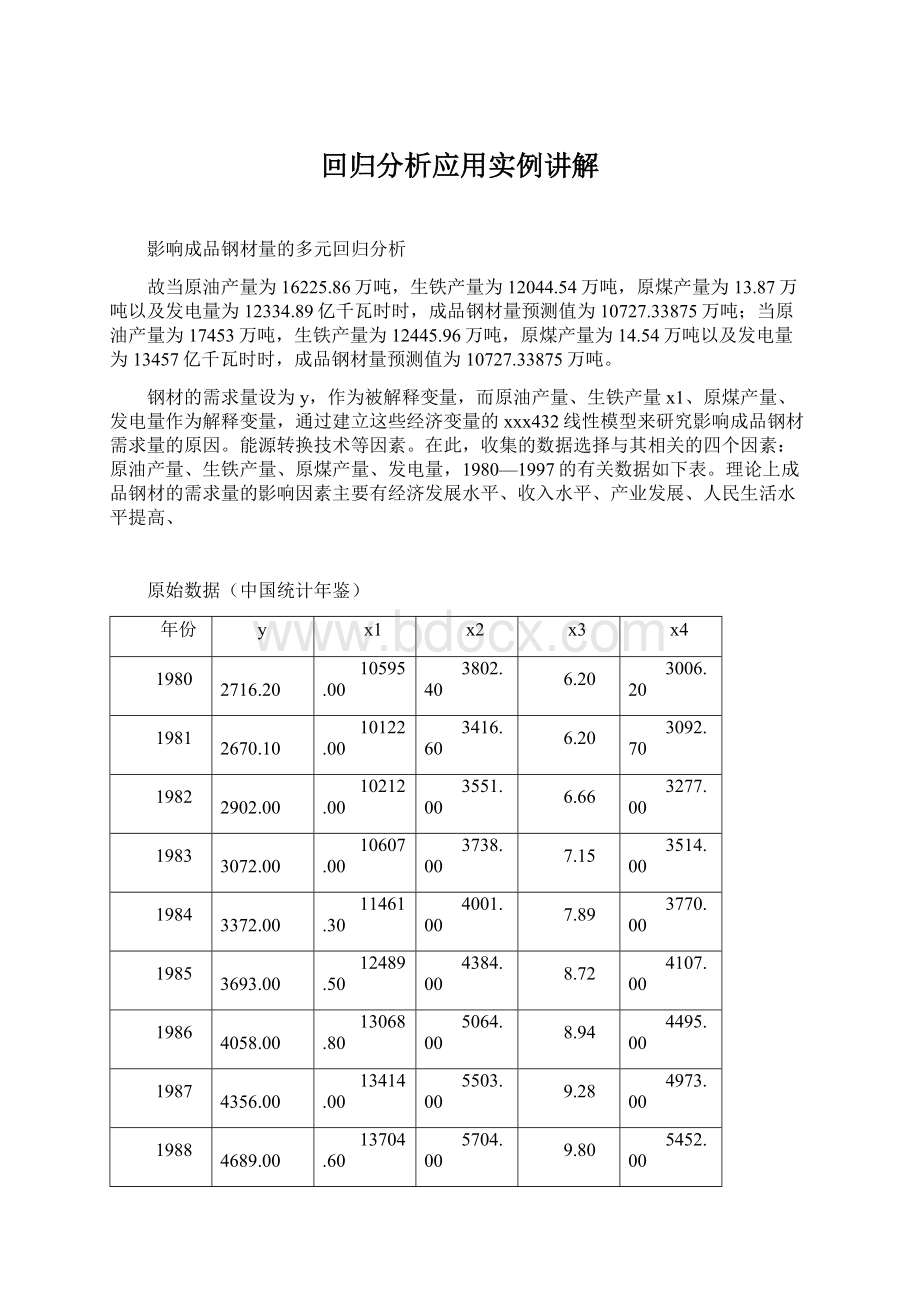
3092.70

1982

2902.00

10212.00

3551.00

6.66

3277.00

1983

3072.00

10607.00

3738.00

7.15

3514.00

1984

3372.00

11461.30

4001.00

7.89

3770.00

1985

3693.00

12489.50

4384.00

8.72

4107.00

1986

4058.00

13068.80

5064.00

8.94

4495.00

1987

4356.00

13414.00

5503.00

9.28

4973.00

1988

4689.00

13704.60

5704.00

9.80

5452.00

1989

4859.00

13764.10

5820.00

10.54

5848.00

1990

5153.00

13830.60

6238.00

10.80

6212.00

1991

5638.00

14009.20

6765.00

10.87

6775.00

1992

6697.00

14209.70

7589.00

11.16

7539.00

1993

7716.00

14523.00

8739.00

11.51

8395.00

1994

8482.00

14608.20

9741.00

12.40

9281.00

1995

8979.80

15004.94

10529.27

13.61

10070.30

1996

9338.02

15733.39

10722.50

13.97

10813.10

1997

9978.93

16074.14

11511.41

13.73

11355.53

将中国成品

一、模型的设定

设因变量y与自变量、、、的一般线性回归模型为:

xxxx4321y=+?

?

x?

xxx?

421330241是随机变量，通常满足；

Var（）=2?

0?

（）?

二参数估计

a系数

模型

非标准化系数

标准系数

t

Sig.

B

标准误差

试用版

）（常量1

）原油（万吨生铁（万吨）原煤（万吨）发电量（亿千瓦时）

170.287-.041.554-17.818.389

494.572.090.170115.468.199

-.031.608-.018.438

.344-.4573.267-.1541.952

.736.655.006.880.073

因变量:

成品钢材（万吨）a.

再用spss做回归线性，根据系数表得出回归方程为：

1x0?

180..?

45x1?

.0?

201y?

7.87x04.5x783894123再做回归预测，得出如下截图：

三回归方程检验

描述性统计量

均值标准偏差N

成品钢材（万吨）182460.349265465.0028

）原油（万吨181875.7887313190.6372

生铁（万吨）18

2700.79676

6489.9544

原煤（万吨）9.96832.5401818

发电量（亿千瓦时）18

2768.11191

6220.8794

相关性

成品钢材（万吨）

原油（万吨）

生铁（万吨）

原煤（万吨）

发电量（亿千瓦时）

成品钢材（万吨）Pearson相关性）原油（万吨生铁（万吨）原煤（万吨）发电量（亿千瓦时）

1.000.909.998.961.997

.9091.000.912.973.920

.998.9121.000.962.997

.961.973.9621.000.971

.997.920.997.9711.000

Sig.（单侧）成品钢材（万吨）原油（万吨）生铁（万吨）原煤（万吨）发电量（亿千瓦时）

..000.000.000.000

.000..000.000.000

.000.000..000.000

.000.000.000..000

.000.000.000.000

成品钢材（万吨）N原油（万吨）生铁（万吨）原煤（万吨）发电量（亿千瓦时）

1818181818

.

由相关系数表看出，因变量与各个自变量的相关系数都很高，都在0.9以上，说明变量间的线性相关程度很高，适合做多元线性回归模型。

b模型汇总

R

R方

调整R方

标准估计的误差

1

a.999

.997

.997

140.71641

a.预测变量:

（常量）,发电量（亿千瓦时）,原油（万吨）,原煤（万吨）,生铁（万吨）。

b.因变量:

成品钢材（万吨）

22R知，模型对样本观测数据的拟合度很好。

由=0.997以及调整之后的=0.997R．

bAnova模型平方和均方Fdf

a回归41296.001

1.026E8.0002.566E7

残差19801.108

13257414.404

总计17

1.029E8

=0.05，故拒绝原假设，认为自变量联合起来值=0.000<

F=1296.001P由对因变量有显著影响，通过F检验。

误差标准

）（常量1）原油（万吨生铁（万吨）原煤（万吨）发电量（亿千瓦时）

a.成品钢材（万吨）因变量:

对因变量?

xt，故接受原假设，认为值=0.880远远大于=0.05因为=-0.154P33y没有显著影响，故应剔除。

用后退法剔除变量后，再做回归线性，x3得如下表：

模型

）常量

（1）原油（万吨生铁（万吨）

170.287-.041.554

494.572.090.170

-.031.608

.344-.4573.267

.736.655.006

原煤（万吨）发电量（亿千瓦时）dAnova模型平方和均方FSig.df

a回归2.566E7.0001.026E841

1296.001

-17.818.389

115.468.199

-.018.438

-.1541.952

.880.073

）常量

（2）原油（万吨生铁（万吨）发电量（亿千瓦时）

197.734-.053.564.371

445.099.045.150.153

-.041.620.417

.444-1.1723.7602.417

.664.261.002.030

）常量（3生铁（万吨）发电量（亿千瓦时）

-309.403.591.311

105.079.150.147

.649.350

-2.9443.9372.125

.010.001.051

成品钢材（万吨）因变量a.:

总计171.029E8

b回归3.422E72

.00031857.513

1.026E8

残差18420.420

14257885.884

c回归5.131E7.0003

2718.023

1.026E82

残差18878.288

15283174.324

b.预测变量:

（常量）,发电量（亿千瓦时）,原油（万吨）,生铁（万吨）。

c.预测变量:

（常量）,发电量（亿千瓦时）,生铁（万吨）。

d.因变量:

、两个自变量，得出新的回归方程为：

xx最后剔除31x0.311x?

0.59