二次函数中寻找等腰三角形问题Word文件下载.docx

二次函数中寻找等腰三角形问题Word文件下载.docx

《二次函数中寻找等腰三角形问题Word文件下载.docx》由会员分享，可在线阅读，更多相关《二次函数中寻找等腰三角形问题Word文件下载.docx（18页珍藏版）》请在冰豆网上搜索。

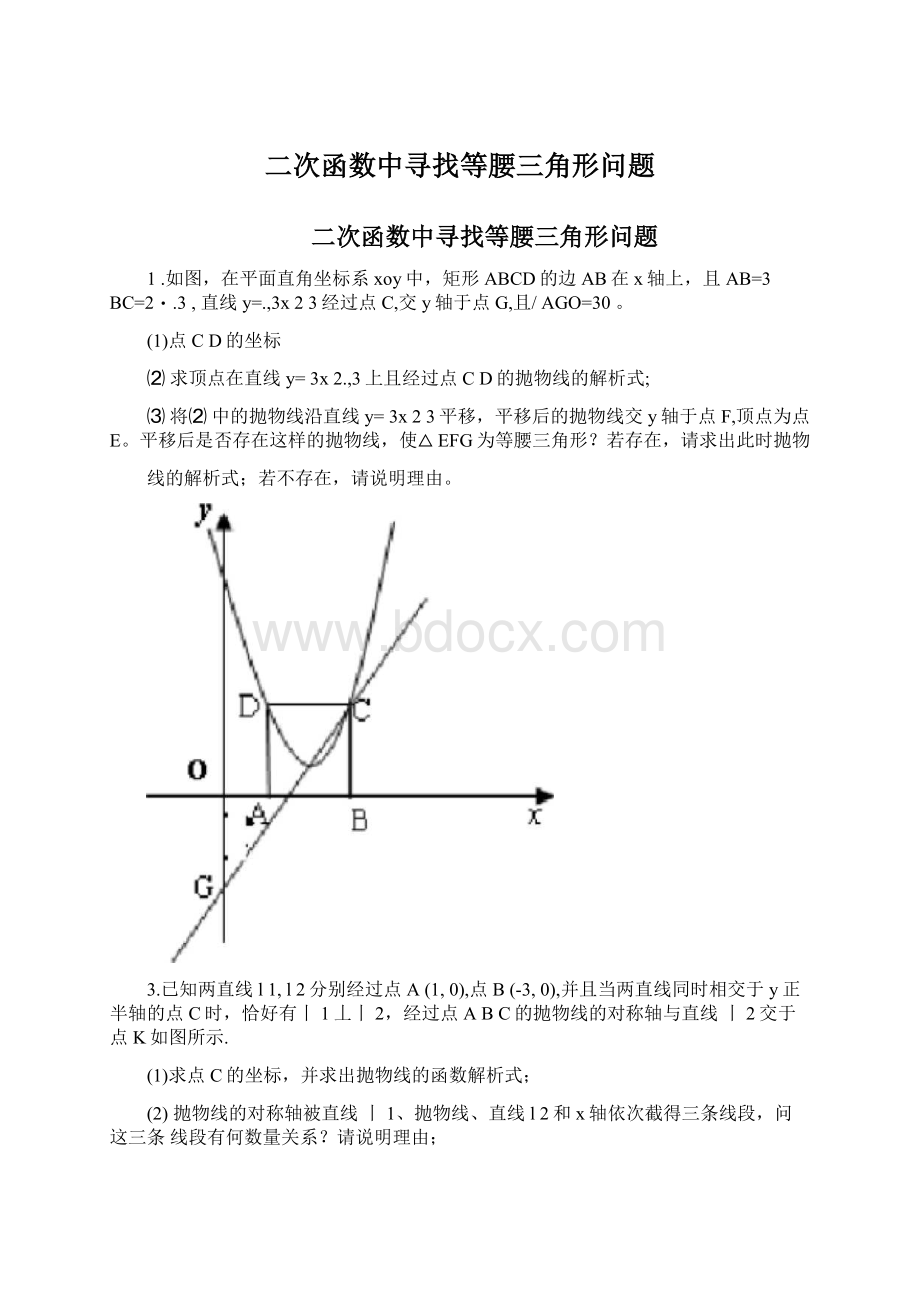
0）的图象经过点B（14,0）和C（0,—8）,对称轴为x=4.

（1）求该抛物线的解析式；

（2）点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的

速度匀速运动，同时另一动点Q以某一速度从C出发沿线段CB匀速运动，问是否存在

某一时刻，使线段PQ被直线CD垂直平分？

若存在，请求出此时的时间t（秒）和点Q

的运动速度；

若不存在，请说明理由；

（3）在

（2）的结论下，直线x=1上是否存在点M使厶MPQ为等腰三角形？

若存在，

_2

6.在平面直角坐标系中，二次函数yaxbx2的图象与x轴交于A（-3,0）,B

（1,0）两点，与y轴交于点C.

（1）求这个二次函数的关系解析式；

（2）点P是直线AC上方的抛物线上一动点，是否存在点只使厶ACP的面积最大？

若

存在，求出点P的坐标；

若不存在，说明理由；

（3）在平面直角坐标系中，是否存在点Q使厶BCQ是以BC为腰的等腰直角三角形？

右存在，直接写出点Q的坐标；

右不存在，说明理由;

7•如图所示，已知抛物线的顶点为坐标原点O,矩形ABCD勺顶点A，D在抛物线上，

且AD平行x轴，交y轴于点F，AB的中点E在x轴上，B点的坐标为（2，1），点P（a，b）在抛物线上运动.（点P异于点O

（1）求此抛物线的解析式.

（2）过点P作CB所在直线的垂线，垂足为点R,

1求证：

PF=PR

2是否存在点P,使得△PFR为等边三角形？

若存在，求出点P的坐标；

若不存在，请

说明理由；

③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线，垂足为S,试判断△RSF

的形状.

C

■F

B

O

E、

A

X

/DF

八

8.在平面直角坐标系xoy中，一块含60°

角的三角板作如图摆放，斜边AB在x轴上,

C三点的抛物

线解析式；

（2）现有与上述三角板完全一样的三角板DEF（其中/EDF=90，/DEF=60）,

把顶点E放在线段

AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C.此时，EF所在直线与

（1）中的抛物线交于第一象限的点M

1设AE=x当x为何值时，△OCOAOBC

2在①的条件下探究：

抛物线的对称轴上是否存在点P使APEM是等腰三角形，若存

在，请求点P的坐标；

若不存在，请说明理由.

9.如图1,在Rt△AOB中，/AOB=90,AO=8j3，/ABO=30.动点P在线段AB上

从点A向终点B以每秒23个单位的速度运动，设运动时间为t秒.在直线0B上取两

点MN作等边△PMN

（1）求当等边厶PMN的顶点M运动到与点0重合时t的值.

（2）求等边△PMN的边长（用t的代数式表示）；

（3）如果取0B的中点D,以0D为边在Rt△AOB内部作如图2所示的矩形ODCE点C在线段AB上.设等边厶PMN和矩形ODCE重叠部分的面积为S,请求出当0<

t<

2秒时S与t的函数关系式，并求出S的最大值.

（4）在（3）中，设PN与EC的交点为R,是否存在点农使厶ODF是等腰三角形？

图2

12

10.如图，已知抛物线yx2bxc与y轴相交于C,与x轴相交于AB,点A的

2

坐标为（2,0）,点C的坐标为（0,-1）.

（1）求抛物线的解析式；

（2）点E是线段AC上一动点，过点E作DEIx轴于点D,连结DC,当厶DCE的面积最

大时，求点D的坐标；

（3）在直线BC上是否存在一点巳使厶ACP为以AC为腰的等腰三角形，若存在，求点

P的坐标，若不存在，说明理由.

参考答案

1.【解析】

（1）根据题意可得点C的纵坐标为3,代入直线解析式可得岀点C的横坐标，继而

也可得岀点D的坐标；

（2）由题意可得点C和点D关于抛物线的对称轴对称，从而得岀抛物线的对称轴为，再由抛物

线的顶点在直线，可得出顶点坐标为（），设出顶点式，代入点C的坐标即可得出答案.

（3）分EF=EGGF=EGGF=EF三种情况分析。

解：

⑴C（4，），D（1，）；

⑵顶点（），解析式；

⑶EF=EG

GF=EG

GF=EF

3.解：

由勾股定理，得（oC+oB）+（oC+oA）=b6+aC=aB，

又•••0B=3OA=1,AB=4,•••°

C=曲，.・.点C的坐标是2'

闪〉

由题意可设抛物线的函数解析式为y=a（x-1）（x+3），把C（0，、彳）代入

fl=，

函数解析式得3

y=-—仪•1/广上丰3丿

所以，抛物线的函数解析式为3

（2）截得三条线段的数量关系为KD=DE=EF

理由如下：

可求得直麓1】的解析式再y=+直建1：

的解析式丸

y二乜；

抛韧無的对称轴为直线EU由此可求得豈K的坐标酋（7洛）,点D的坐标为（-1,坯），点E的坐标为（-1,点F的坐标肯【70）—

C-（-It—

（3）当点M的坐标分别为时，△MCK为等腰三角形.

（i）连接BK交抛物线于点G,易知点G的坐标为（-2,

又•••点C的坐标为（0,•••可求得AB=BK=4且/ABK=60，即△ABK为正三角形,

•••△CGK为正三角形

•••当12与抛物线交于点G,即12/AB时，符合题意，此时点

2x3

（ii）连接CD由KD=h,CK=CG=2/CKD=30，易知△KDC为等腰三角形,

•••当12过抛物线顶点D时，符合题意，此时点M2坐标为（-1,）,

（iii）当点M在抛物线对称轴右边时，只有点M与点A重合时，满足CM=CK

但点ACK在同一直线上，不能构成三角形，

宀（-2,J3）,（-1,埠）

综上所述，当点M的坐标分别为'

时，△MCK为等腰三角形.

4.

（1）设y=ax（x-4）,把A点坐标（3,3）代入得：

a=-1,

函数的解析式为y=-x2+4x,

（2）0<

3,

（3）P的坐标是（3-.:

1+2.」）或（3+】:

1-2敖|）或（5,-5）或（4,0）.

12分

（3）简单解答过程如下:

•••W.|

当m>

3时，PC=CD-PD=m—3mOC颌口，

由勾股定理得：

Op=oD+Dp=m+m（m-4）2,

1当OC=PC寸，「-.,

解得：

2当OC=O时，〔一-'

'

.T-1

m=5,m=3（舍去），

二P（5,-5）；

3当PC=OP寸，m2（m-3）2=m2+m2（m-4）2,

m=4二P（4,0）,

存在P的坐标是（3-.■:

1+2.一：

）或（3+二，1-2.二）或（5,-5）或（4,0）.

（2）存在，理由如下:

■-X1-垂直平分珀…'

.'

AD-ACt-'

-ZADC=^ACD,

■'

■dCCL0?

在取△曲C中，dC=7^0+CC2--10>

AP=1Q.又肌尸&

，・：

QDN,卩

「・卫在^寸称轴上根据对称性可知ALFDiZ.A8DQ*&

Q为EC的中

在RtABOC中，胆"

X4■朋=2屈，二笑二届，TD、Q为ABrM的中点，-'

.

型=*卫—52

—DFQMDQF、「-皿=匹=门4尸二jW-M：

工「•『=罕=亍・二卩「=字=寧，4

（d）设F陋=./l+ir-D）=血\yj五+0X）=&

斗卩+刃,尸鸟=M

1°

当F0FH时，诈・&

+3』二』・±

2逅，二M（l,20〉」-2西）2

胪当F4QM时，勒5土&

十旳卄比，・・・j=Y±

2』T,/.M（lT-4-F2jT>

JiJ.（W-2jT）-

3*当PI=QM时，$=-6,/-if（1,-6）^

卫帧（1—+2厲少口7-2航）.-外综上所述：

存在5个M点，即

6.【解析】解：

（1由抛物线过A（-3,0）,B（1,0）,贝9

，解得。

•••二次函数的关系解析式为。

（2）设点P坐标为（mn）,贝0。

连接PO,作PMLx轴于MPN丄y轴于N。

PM=,,A0=3

当时，，所以OC=2

111

tv0,•函数有最大值，当时，有最大值。

此时。

•存在点，使△ACP的面积最大。

（3）存在。

点

7.【解析】解：

（1）v抛物线的顶点为坐标原点，•••A、D关于抛物线的对称轴对称

•/E是AB的中点，•O是矩形ABCD寸角线的交点

又•••B（2,1）,二A（2,—1）、D（-2,—1）。

•••抛物线的顶点为（0,0）,二可设其解析式为：

y=ax，则有：

4a=—1,a=—

•抛物线的解析式为：

y=-x2。

（2）①证明：

由抛物线的解析式知：

P（a,—a），而R（a,1）、F（0,—1）,

则：

PF=

PR=,

•PF=PR

②•••RF=,「.若厶PFR为等边三角形，则由①得RF=PF=PR得:

=，即：

a4—8a2—48=0，得：

a2=—4（舍去），a2=12。

2

•a=±

2,—a=—3。

•••存在符合条件的P点，坐标为（2,—3）、（-2,—3）。

③同①可证得：

QF=QS

在等腰△SQF中，/1=（180°

-/SQF）。

同理，在等腰RPF中，/2=（180°

—/RPF）。

•/QSLBCPR!

BC,•QS//PR,/SQP/RPF=180