框架式塔设备的设计Word下载.docx

框架式塔设备的设计Word下载.docx

《框架式塔设备的设计Word下载.docx》由会员分享，可在线阅读，更多相关《框架式塔设备的设计Word下载.docx（9页珍藏版）》请在冰豆网上搜索。

符号:

qi—

——塔设备第i计算段的风压;

Pi———塔设备第i计算段的水平风力;

li———塔设备第i计算段的长度;

EIi———塔设备第i计算段的抗弯刚度;

H———塔设备总高度;

Qi-1———塔设备第i计算段受到第i-1段对它的剪力;

Mi-1———塔设备第i计算段受到第i-1段对它的弯矩;

yi———塔设备第i计算段顶部在Pi、Qi-1、Mi-1下的挠度;

θi———塔设备第i计算段顶部在Pi、Qi-1、Mi-1下的转角;

w

i-1

———塔顶由塔设备第i计算段由θi引起的挠度;

Y———塔设备无框架时,塔顶的挠度;

Y’———塔设备有框架时,塔顶的挠度;

[Y]———塔设备塔顶的许用挠度。

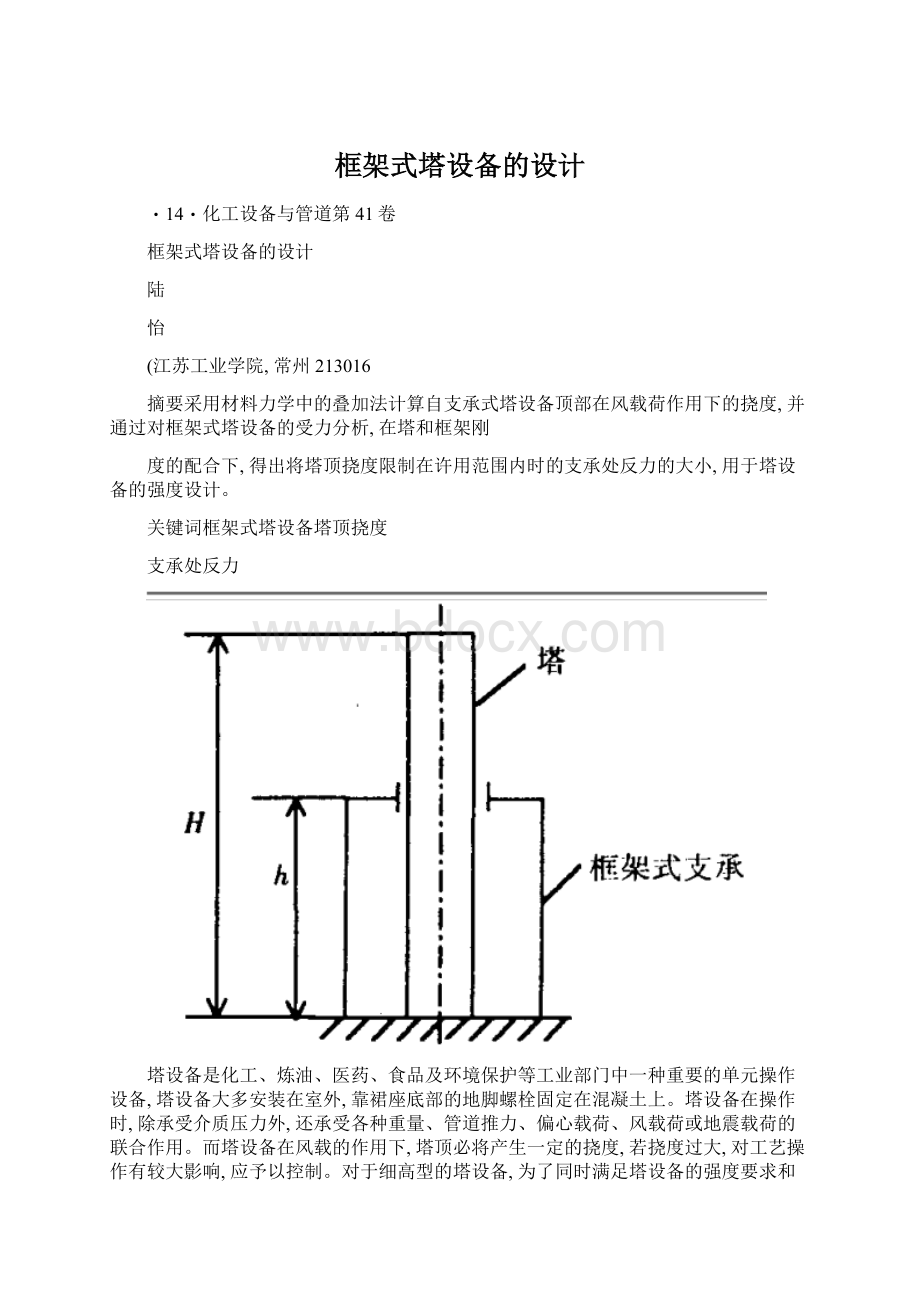
图1框架式支承塔结构示意图

1自支承式塔设备塔顶挠度计算

由于随着高度不同,塔设备各段所受的力也不

同[1],因此塔顶的挠度难以用一端固支梁在均布载荷下的挠度公式求出,须将塔设备分成若干段,把每一段看作是一端固支的悬臂梁,进行受力分析,然后按照材料力学[2]中的叠加原理计算塔顶的挠度。

塔设备受力及变形情况如图2所示。

（a无框架塔设备受力

（b框架式塔设备受力

图2

塔设备受力及变形分析示意图

・15・

2004年第1期（下转第18页

从图中可以看出,自支承式无框架塔设备塔顶的挠度为

Y=y1+y2+y3+…yi+w1+w2+…

wi-1（1

其中wi-1是由第i段顶部转角引起的,求法在图2中已经标出,yi和θi可以用固支梁在简单载荷下的变形加以叠加,对第i计算段中,Pi、Qi-1、Mi-1可以看作该段上的三种简单载荷,因此可以运用叠加原理进行叠加,叠加方程如表1所示。

表1梁在简单载荷作用下的变形

梁的简图

端截面转角

自由端挠度

3

6EI=

26EI（

P=ql4

8EI=

38EI

22EI33EIEI

22EI

由于yi、θi是由Pi、Qi-1、Mi-1引起的,所以

yi=

i

2

EIi8+3+

（2θi=

EIi

6+

+Mi-

（3

已知Pi=qili,剪力Qi-1、弯矩Mi-1可以由静力

平衡方程求得。

即由力平衡Q1=P1,Q2=Q1+P2,Q3=Q2+P3,依次类推

Qi-1=Qi-2+Pi-1

（4

由力矩平衡,M1=P1l1/2,M2=P2l2/2+Q1l2+M1,

M3=P3l3/2+Q2l3+M2,依次类推

Mi-1=Pi-1li-1/2+Qi-2li-1+Mi-2

（5将式（4、（5代入（2、（3,求出yi、θi,再代入（1式,就可以得到自支承式无框架塔设备塔顶的挠度。

2框架式塔设备受力分析

与自支承式塔设备相比,框架式塔设备在支承

位置受到了框架的约束,增加了支反力的作用,因此在强度计算时有所不同,必须考虑在内。

两种塔设备的受力情况如图3所示。

可以看出,（a图中塔设备在自支承时,A处无支承,受支反力N=0,塔顶挠度可由（1式求出,如果塔设备为细高塔（DN<

1m,且H/DN>

25,或DN>

30[3]

此挠度往往过大,超过许用

值。

由于塔设备的挠度曲线可近似为抛物线,此时

L1=

H

Y2

而（b图中,塔设备采用框架支承,A处受到约束反力N的作用,挠度受到了限制,此时塔顶挠度Y’也随之减小。

因此采用框架支承,只要框架刚度适当,就可以将塔设备的塔顶挠度控制在许用范围内,即Y’≤[Y]。

图3

采用材料力学方法,利用变形协调关系,可以获

得支反力N,塔设备刚度K1及框架刚度K2,塔顶挠度

Y之间的关系。

（a图中,N=0,支点A处塔的挠度L1是由风载P产生的,此处P=K1L1

（6

（b图中,N≠0,支点A处塔的挠度L2是由风载

P和支反力N共同产生的,故

P-N=K1L2,

（7而此时框架上A处受到反作用的支反力,由变形协

调,该框架挠度也为L2,并满足N=K2L2

（8（6、（7、（8三式联立,得到N=

K1+K2

L1

L2=

K1+K2H

Y

（9

当要求Y’≤[Y]时,只要使L2≤[L],[L]=H

[Y]2。

因此L2=K1+K2

K1+K2HY2

[Y]

2即

≤[Y]

2（10

从式（10可以看出,只要调整塔设备刚度K1及框架刚度K2,就能使塔设备满足挠度要求。

由于塔设备刚度K1与壁厚相关,而壁厚又与受力情况及强度设计相关,当K1、K2未定时,支反力就无法确定。

因此,塔设备刚度K1及框架刚度K2的调整有一个过程,需要反复计算,以使两者达到比（a

（b

・18・化工设备与管道第41卷

的直径增大而呈逐渐减小的趋势。

直径为195mm时的最大第一主应力为42.1MPa,而直径为155时为68.5MPa,二者相差较大。

而在管道内壁上,第一主应力值的却随着补强板直径的增加而呈增大的趋势,但是增加的幅度要小于外壁上随着直径增大而减小的幅度。

从应力强度的角度看,在管道内壁上,随着补强板直径的改变,应力强度的值变化不大,直径为195mm的补强板对应的结果稍大。

而从管道外壁上的应力强度值看,随着补强板直径的增大,管道外壁上的应力强度值呈增大的趋势,且变化的趋势较明显。

因此,综合第一主应力和应力强度的分布结果看,对于一定厚度的补强板,采用尺寸较小的补强板应该更为合理,小尺寸的补强板可以减小管道内壁上第一主应力值和减小管道外壁上的应力强度值。

3补强板厚度对补强效果的影响

3.1模型的描述

计算中采用的基本尺寸为,管道:

<

325×

10mm,

总长度取为10000mm;

支耳:

89×

5.5mm,总长度取为400mm;

补强板:

补强板的尺寸采用圆形补强板,它的中间开孔,孔的直径要比支耳管的内径略大,在保证其直径为195mm的前提下,取补强板的三种厚度分别为7mm、10mm、13mm。

由于计算中采用的管道和支耳管的尺寸跟上一小节相同,并且不计管道内液体的内压,所以本节模型上所施加的载荷以及约束跟前小节相同。

网格采用规则的六面体划分,单元仍然选择SOLID45八节点实体单元。

3.2计算结果分析

可以看到,对于直径一定的补强板,增加补强板的厚度,可以明显的改善管道外壁上的第一主应力

的最大值,管道外壁上的最大第一主应力随着补强板壁厚的增加而呈逐渐减小的趋势。

但是对于管道内壁上的第一主应力值,补强板壁厚的影响效果甚微。

从管道上应力强度的分布趋势来看,随着补强板厚度的增加,管道内外壁上的应力强度值都随之减小,就是说对于一定直径的补强板,采用较厚尺寸可以明显的改善管道内外壁上的应力强度分布情况。

可见,对于直径一定的补强板,要想提高补强的效果,应该优先考虑厚度大的补强板,以利于提高补强的效果。

表3在不同厚度补强板的补强下,主管上的最大应力值

补强板的直径（mm最大第一主应力值（MPa和出现位置

最大应力强度值（MPa

和出现位置

783.7（管道外壁上118（管道外壁上41.4（管道内壁上85.7（管道内壁上1062.3（管道外壁上91.6（管道外壁上42.17（管道内壁上62.8（管道内壁上13

52.9（管道外壁上72.1（管道外壁上40.8（管道内壁上46.1（管道内壁上

4结论

（1存在承重性支耳的管道除了在管道和支耳

交接位置处管道外壁上存在着很大的应力集中之外,在管道的内壁上也出现了应力强度和第一主应力很大的区域。

（2补强板的采用不仅使得管道外壁上的应力

集中的情况得到很好的改善,同时也会大大改善了管道内壁上的应力分布状况。

（3对于厚度一定的补强板来说,采用较小尺寸的补强板可以得到相对较好的补强效果。

（4对于同一直径的圆形补强板来说,它的厚度

越大,它对管道的补强效果就会越好。

（上接第15页

较理想的配合。

然后再计算出框架处支反力,画出塔设备的弯矩图,对塔设备进行强度计算,确定壁厚。

3结束语

两种类型的塔设备结构不同,因此受力不同,在设计时必须根据实际情况加以区分,选用适合的方法进行。

参考文献

1郑津洋,董其伍,桑芝富,过程装备设计[M],北京:

化学工业出版

社,2001.348～349

2刘鸿文,材料力学（上册[M].北京:

高等教育出版社,1987.235～244

41.483.742.

1762.

・3

・

Vol.41No.1