高中数学湘教版必修1第二章 指数函数对数函数和幂函数231232Word文件下载.docx

高中数学湘教版必修1第二章 指数函数对数函数和幂函数231232Word文件下载.docx

《高中数学湘教版必修1第二章 指数函数对数函数和幂函数231232Word文件下载.docx》由会员分享，可在线阅读，更多相关《高中数学湘教版必修1第二章 指数函数对数函数和幂函数231232Word文件下载.docx（12页珍藏版）》请在冰豆网上搜索。

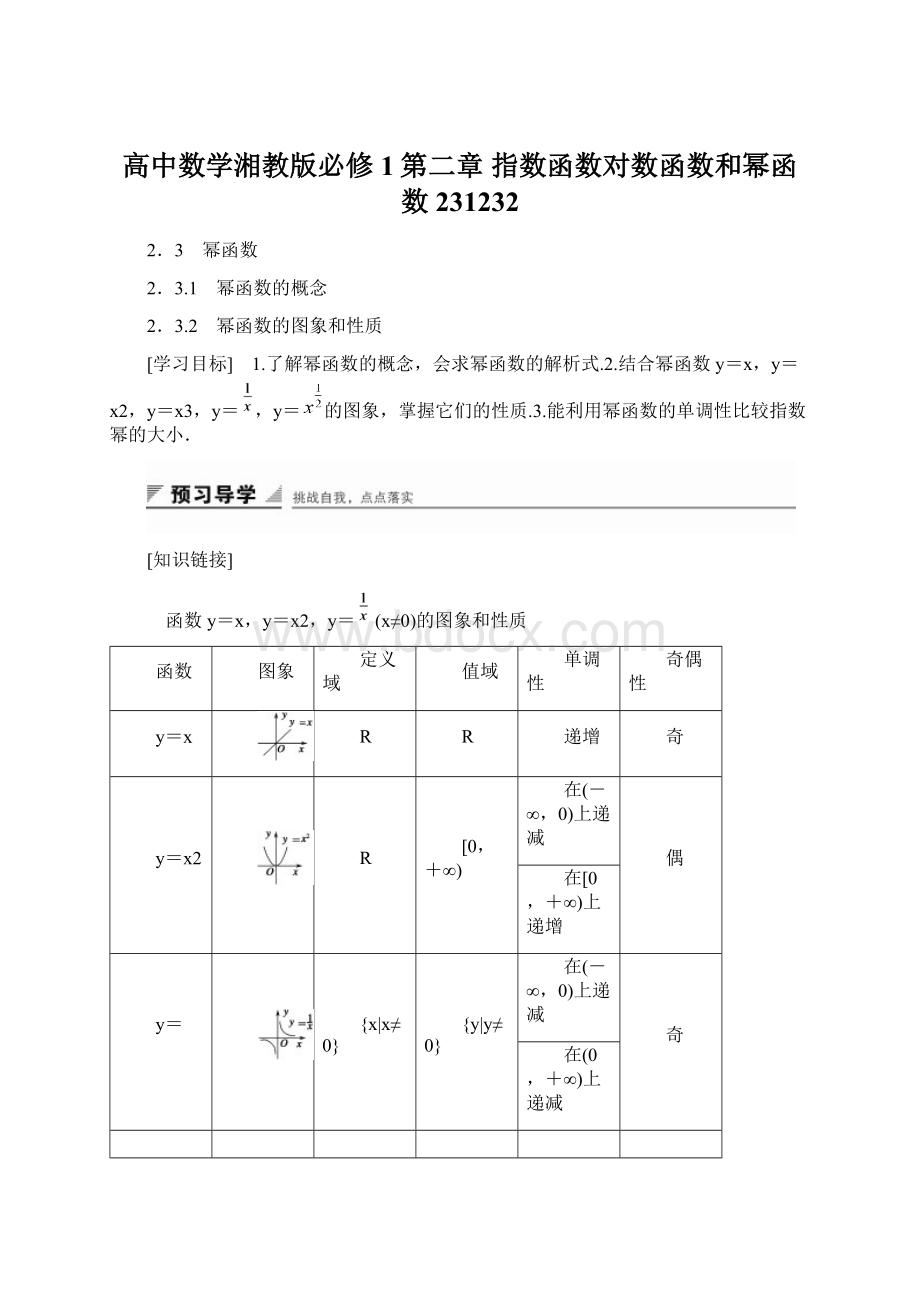
偶

在[0，＋∞）上递增

y＝

{x|x≠0}

{y|y≠0}

在（0，＋∞）上递减

[预习导引]

1．幂函数的概念

一般来说，当x为自变量而α为非0实数时，函数y＝xα叫作（α次的）幂函数．

2．幂函数的图象与性质

幂函数

y＝x3

y＝x－1

（－∞，0）∪（0，＋∞）

{y|y∈R，且y≠0}

非奇非偶

x∈[0，＋∞）递增；

x∈（－∞，0]递减

x∈（0，＋∞）递减；

x∈（－∞，0）递减

定点

（1,1）

要点一　幂函数的概念

例1　函数f（x）＝（m2－m－1）xm2＋m－3是幂函数，且当x∈（0，＋∞）时，f（x）是增函数，求f（x）的解析式．

解　根据幂函数定义得，

m2－m－1＝1，解得m＝2或m＝－1，

当m＝2时，f（x）＝x3，在（0，＋∞）上是增函数，

当m＝－1时，f（x）＝x－3，在（0，＋∞）上是减函数，不合要求．

∴f（x）的解析式为f（x）＝x3.

规律方法　1.本题在求解中常因不理解幂函数的概念而找不出“m2－m－1＝1”这一等量关系，导致解题受阻．

2．幂函数y＝xα（α∈R）中，α为常数，系数为1，底数为单一的x.这是判断一个函数是否为幂函数的重要依据和唯一标准．幂函数与指数函数的解析式形同而实异，解题时一定要分清，以防出错．

跟踪演练1　已知幂函数f（x）＝xα的图象经过点（9,3），则f（100）＝________.

答案　10

解析　由题意可知f（9）＝3，即9α＝3，

∴α＝，∴f（x）＝，∴f（100）＝＝10.

要点二　幂函数的图象

例2　如图所示，图中的曲线是幂函数y＝xn在第一象限的图象，已知n取±

2，±

四个值，则相应于c1，c2，c3，c4的n依次为（　　）

A．－2，－，，2　　　　　B．2，，－，－2

C．－，－2,2，D．2，，－2，－

答案　B

解析　考虑幂函数在第一象限内的增减性．注意当n＞0时，对于y＝xn，n越大，y＝xn增幅越快，n＜0时看|n|的大小．根据幂函数y＝xn的性质，在第一象限内的图象当n＞0时，n越大，y＝xn递增速度越快，故c1的n＝2，c2的n＝，当n＜0时，|n|越大，曲线越陡峭，所以曲线c3的n＝－，曲线c4的n＝－2，故选B.

规律方法　幂函数图象的特征：

（1）在第一象限内，直线x＝1的右侧，y＝xα的图象由上到下，指数α由大变小；

在第一象限内，直线x＝1的左侧，y＝xα的图象由上到下，指数α由小变大．

（2）当α＞0时，幂函数的图象都经过（0,0）和（1,1）点，在第一象限内，当0＜α＜1时，曲线上凸；

当α＞1时，曲线下凸；

当α＜0时，幂函数的图象都经过（1,1）点，在第一象限内，曲线下凸．

跟踪演练2　如图是幂函数y＝xm与y＝xn在第一象限内的图象，则（　　）

A．－1＜n＜0＜m＜1

B．n＜－1,0＜m＜1

C．－1＜n＜0，m＞1

D．n＜－1，m＞1

解析　在（0,1）内取同一值x0，作直线x＝x0，与各图象有交点，如图所示．根据点低指数大，有0＜m＜1，n＜－1.

要点三　比较幂的大小

例3　比较下列各组数中两个数的大小：

（1）与；

（2）－1与－1；

（3）0.25与6.25；

（4）0.20.6与0.30.4.

解　

（1）∵y＝是[0，＋∞）上的增函数，且＞，

∴＞.

（2）∵y＝x－1是（－∞，0）上的减函数，且－＜－，

∴－1＞－1.

（3）0.25＝＝2，6.25＝2.5.

∵y＝x是[0，＋∞）上的增函数，且2＜2.5，

∴2＜2.5，即0.25＜6.25.

（4）由幂函数的单调性，知0.20.6＜0.30.6，又y＝0.3x是减函数，∴0.30.4＞0.30.6，从而0.20.6＜0.30.4.

规律方法　1.比较幂值的大小，关键在于构造适当的函数：

（1）若指数相同而底数不同，则构造幂函数；

（2）若指数不同而底数相同，则构造指数函数．

2．若指数与底数都不同，需考虑是否能把指数或底数化为相同，是否可以引入中间量．

跟踪演练3　比较下列各组数的大小：

（1）0.5与0.5；

（2）－3.143与－π3；

（3）与.

解　

（1）∵y＝x0.5在[0，＋∞）上是增函数且＞，

∴0.5＞0.5.

（2）∵y＝x3是R上的增函数，且3.14＜π，

∴3.143＜π3，∴－3.143＞－π3.

（3）∵y＝x是减函数，∴＜.

y＝是[0，＋∞）上的增函数，

∴＞.∴＞.

1．下列函数是幂函数的是（　　）

A．y＝5x　　　　　　　　B．y＝x5

C．y＝5xD．y＝（x＋1）3

解析　函数y＝5x是指数函数，不是幂函数；

函数y＝5x是正比例函数，不是幂函数；

函数y＝（x＋1）3的底数不是自变量x，不是幂函数；

函数y＝x5是幂函数．

2．下列函数中，其定义域和值域不同的函数是（　　）

A．y＝B．y＝x

C．y＝D．y＝x

答案　D

解析　y＝x＝，其定义域为R，值域为[0，＋∞），故定义域与值域不同．

3．设α∈，则使函数y＝xα的定义域为R且为奇函数的所有α值为（　　）

A．1,3B．－1,1

C．－1,3D．－1,1,3

答案　A

解析　可知当α＝－1,1,3时，y＝xα为奇函数，又∵y＝xα的定义域为R，则α＝1,3.

4．若a＝（），b＝（），c＝（－2）3，则a、b、c的大小关系为________．

答案　a＞b＞c

解析　∵y＝x在（0，＋∞）上为增函数．

∴（）＞（），即a＞b＞0.

而c＝（－2）3＝－23＜0，∴a＞b＞c.

5．幂函数f（x）＝（m2－m－1）·

xm2－2m－3在（0，＋∞）上是减函数，则实数m＝________.

答案　2

解析　∵f（x）＝（m2－m－1）xm2－2m－3为幂函数，

∴m2－m－1＝1，∴m＝2或m＝－1.

当m＝2时，f（x）＝x－3在（0，＋∞）上是减函数，

当m＝－1时，f（x）＝x0＝1不符合题意．

综上可知m＝2.

1.幂函数y＝xα的底数是自变量，指数是常数，而指数函数正好相反，底数是常数，指数是自变量．

2．幂函数在第一象限内指数变化规律

在第一象限内直线x＝1的右侧，图象从上到下，相应的指数由大变小；

在直线x＝1的左侧，图象从下到上，相应的指数由大变小．

3．简单幂函数的性质

（1）所有幂函数在（0，＋∞）上都有定义，并且当自变量为1时，函数值为1，即f

（1）＝1.

（2）如果α＞0，幂函数在[0，＋∞）上有意义，且是增函数．

（3）如果α＜0，幂函数在x＝0处无意义，在（0，＋∞）上是减函数.

一、基础达标

1．已知幂函数f（x）的图象经过点，则f（4）的值为（　　）

A．16B.

C.D．2

答案　C

解析　设f（x）＝xα，则有2α＝，解得α＝－，即f（x）＝x，所以f（4）＝4＝.

2．下列命题中正确的是（　　）

A．当α＝0时，函数y＝xα的图象是一条直线

B．幂函数的图象都经过（0,0）（1,1）两点

C．若幂函数y＝xα的图象关于原点对称，则y＝xα在定义域上是增函数

D．幂函数的图象不可能在第四象限

解析　当α＝0时，函数y＝xα的定义域为{x|x≠0，x∈R}，其图象为两条射线，故A选项不正确；

当α＜0时，函数y＝xα的图象不过（0,0）点，故选项B不正确；

幂函数y＝x－1的图象关于原点对称，但其在定义域内不是增函数，故选项C不正确；

当x＞0，α∈R时，y＝xα＞0，则幂函数的图象都不在第四象限，故选项D正确．

3．下列幂函数中①y＝x－1；

②y＝x；

③y＝x；

④y＝x2；

⑤y＝x3，其中在定义域内为增函数的个数为（　　）

A．2B．3C．4D．5

解析　由幂函数性质知②③⑤在定义域内为增函数．

4．当0＜x＜1时，f（x）＝x2，g（x）＝x，h（x）＝x－2的大小关系是（　　）

A．h（x）＜g（x）＜f（x）B．h（x）＜f（x）＜g（x）

C．g（x）＜h（x）＜f（x）D．f（x）＜g（x）＜h（x）

解析　在同一坐标系中，画出当0＜x＜1时，函数y＝x2，y＝x，y＝x－2的图象，如图所示．

∴当0＜x＜1时，有x－2＞x＞x2，

即f（x）＜g（x）＜h（x）．

5．下列函数中，既是偶函数，又在区间（0，＋∞）上单调递减的函数是（　　）

A．y＝x－2B．y＝x－1

C．y＝x2D．y＝

解析　由于y＝x－1和y＝都是奇函数，故B、D不合题意．又y＝x2虽为偶函数，但在（0，＋∞）上为增函数，故C不合题意．y＝x－2＝在（0，＋∞）上为减函数，且为偶函数，故A满足题意．

6．幂函数y＝f（x）的图象经过点（2，），则满足f（x）＝－27的x值等于________．

答案　－

解析　设f（x）＝xα，由题意可知2α＝，α＝－3，

即f（x）＝x－3.

由x－3＝－27可知x＝－.

7．比较下列各组中两个值的大小：

（1）1.5与1.6；

（2）0.61.3与0.71.3；

（2）3.5与5.3；

（4）0.18－0.3与0.15－0.3.

解　

（1）∵幂函数y＝x在（0，＋∞）上单调递增，且1.5＜1.6，∴1.5＜1.6.

（2）∵幂函数y＝x1.3在（0，＋∞）上单调递增，且0.6＜0.7，∴0.61.3＜0.71.3.

（3）∵幂函数y＝x在（0，＋∞）上单调递减，且3.5＜5.3，∴3.5＞5.3.

（4）∵幂函数y＝x－0.3在（0，＋∞）上单调递减，且0.18＞0.15，∴0.18－0.3＜0.15－0.3

二、能力提升

8．设a＝，b＝，c＝，则a，b，c的大小关系是（　　）

A．a＞b＞cB．c＞a＞b

C．a＜b＜cD．b＞c＞a

解析　∵函数y＝x在R上是减函数，又＞，

∴＜，即a＜b.

又∵函数y＝x在R上是增函数，且＞，

∴＞，即c＞b，

∴a＜b＜c.

9．函数y＝的图象是（　　）

解析　方法一　代入选项验证即可．

方法二　y＝＝＝－＋1，利用函数图象的变换可知选B.

10．若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”．那么函数解析式为f（x）＝x2，值域为{1,4}的“同族函数”共有（　　）

A．7个B．8个C．9个D．无数个

解析　值域为{1,4}，∴其定义域由1，－1,2，－2组成，∴有{1,2}，{1，－2}，{－1,2}，{－1，－2}，{1，－1，－2}，{1，－