高三数学当堂训练 空间几何体的结构特征及三视图与直观图.docx

高三数学当堂训练 空间几何体的结构特征及三视图与直观图.docx

《高三数学当堂训练 空间几何体的结构特征及三视图与直观图.docx》由会员分享，可在线阅读，更多相关《高三数学当堂训练 空间几何体的结构特征及三视图与直观图.docx（11页珍藏版）》请在冰豆网上搜索。

高三数学当堂训练空间几何体的结构特征及三视图与直观图

第七章　立体几何

高三数学当堂训练空间几何体的结构特征及三视图与直观图

一、选择题

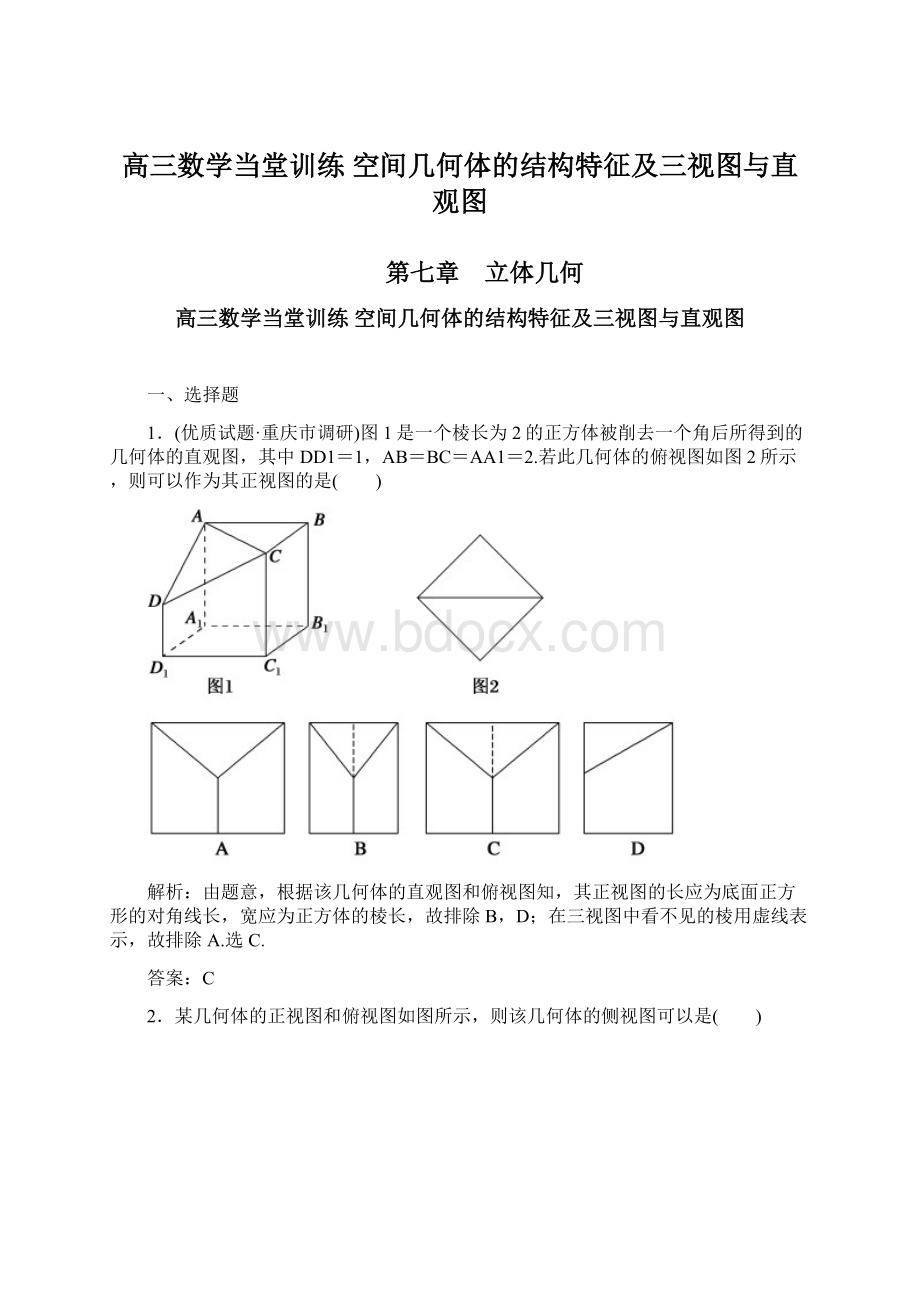
1．（优质试题·重庆市调研）图1是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中DD1＝1，AB＝BC＝AA1＝2.若此几何体的俯视图如图2所示，则可以作为其正视图的是（　　）

解析：

由题意，根据该几何体的直观图和俯视图知，其正视图的长应为底面正方形的对角线长，宽应为正方体的棱长，故排除B，D；在三视图中看不见的棱用虚线表示，故排除A.选C.

答案：

C

2．某几何体的正视图和俯视图如图所示，则该几何体的侧视图可以是（　　）

解析：

由几何体的正视图与俯视图可知，该几何体是四棱锥PABFH挖去一个三棱锥PCDE后得到的几何体，其中四棱锥的侧面PAH与底面ABFH垂直，如图所示．显然该几何体的侧视图是一个三角形，而棱PD在侧视图投影面上的射影应为一条虚线，故排除B，D；显然D点在侧视图投影面上的射影与底面ABFH的射影在一条直线上，故排除A.选C.

答案：

C

3．（优质试题·浙江卷）某几何体的三视图如图所示（单位：

cm），则该几何体的体积（单位：

cm3）是（　　）

A.＋1　　　　B.＋3

C.＋1　　　　D.＋3

解析：

通过分析三视图可知，该几何体是一个三棱锥与一个半圆锥的组合体，由主视图可知该组合体的高为3，底面是一个底边长为2的等腰直角三角形与半径为1的半圆，所以该几何体的体积V＝×3×＝＋1（cm3）．故选A.

答案：

A

4．（优质试题·新课标全国卷Ⅱ）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（　　）

A．90πB．63π

C．42πD．36π

解析：

解法1：

由三视图可知，该几何体是一个圆柱被一个平面从上底面边缘斜向下45°截取后得到的，但是被截得的几何体并不是圆锥，故其不能用锥体公式求解，由于截面的倾斜角为45°，恰巧将上部分的圆柱平均分成完全相等的两部分，故该几何体的体积是π×32×4＋＝36π＋27π＝63π.故选B.

解法2：

如图所示，将一个相同的几何体拼接在原几何体上，得到的新的几何体是底面半径为3，高为14的圆柱，故原几何体的体积是此圆柱的体积的一半．V圆柱＝πr2h＝π×32×14＝126π，所以V原几何体＝V圆柱＝63π.

答案：

B

5．（优质试题·中原名校质检）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（　　）

A．9（＋1）π＋8B．9（＋2）π＋4－8

C．9（＋2）π＋4D．9（＋1）π＋8－8

解析：

由三视图可知，该几何体是由一个四棱锥和一个圆锥拼接而成，故S＝×（2π×3）×3＋π×32－

（2）2＋4×＝9（＋1）π＋8－8.故选D.

答案：

D

6．（优质试题·湖南永州一模）如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的各个面中最大面的面积为（　　）

A．1　　　　B.　　　　C.　　　　D．2

解析：

由题意得，该几何体的直观图为三棱锥ABCD，如图，其最大面的表面是边长为2的等边三角形，其面积为×

（2）2＝2.

答案：

D

二、填空题

7．用一个平行于圆锥底面的平面截这个圆锥，截得的圆台上、下底面的面积之比为116，截去的圆锥的母线长是3cm，则圆台的母线长为________cm.

解析：

由圆台上、下底面积之比为116，设圆台上下底面的半径分别为r,4r.圆台的母线长为l，根据相似三角形的性质得＝，解得l＝9.

答案：

9

8．（优质试题·福建龙岩联考）一水平放置的平面四边形OABC，用斜二测画法画出它的直观图O′A′B′C′如图所示，此直观图恰好是一个边长为1的正方形，则原平面四边形OABC面积为________．

解析：

因为直观图的面积是原图形面积的倍，且直观图的面积为1，所以原图形的面积为2.

答案：

2

9．（优质试题·山东卷）由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为________．

解析：

由组合体及三视图中的数据可知，圆柱体的底面半径为1，高为1，长方体的长、宽、高分别为2,1,1，所以组合体的体积为V＝2×1×1＋2××π×12＝2＋.

答案：

2＋

10．如图，点O为正方体ABCDA′B′C′D′的中心，点E为面B′BCC′的中心，点F为B′C′的中点，则空间四边形D′OEF在该正方体的各个面上的正投影可能是________（填出所有可能的序号）．

解析：

空间四边形D′OEF在正方体的面DCC′D′及其对面ABB′A′上的正投影是①；在面BCC′B′及其对面ADD′A′上的正投影是②；在面ABCD及其对面A′B′C′D′上的正投影是③.

答案：

①②③

1．（优质试题·福建泉州二模）某几何体的三视图如图所示，则该几何体的侧视图中的虚线部分是（　　）

A．圆弧B．抛物线的一部分

C．椭圆的一部分D．双曲线的一部分

解析：

根据几何体的三视图可得，侧视图中的虚线部分是由平行于旋转轴的平面截圆锥所得，故侧视图中的虚线部分是双曲线的一部分．故选D.

答案：

D

2．一个四面体的顶点都在球面上，它们的正视图、侧视图、俯视图都是下图．图中圆内有一个以圆心为中心边长为1的正方形，则这个四面体的外接球的表面积是（　　）

A．πB．3π

C．4πD．6π

解析：

由三视图可知：

该四面体是正方体的一个内接正四面体．∴此四面体的外接球的直径为正方体的对角线长为.

∴此四面体的外接球的表面积为4π×（）2＝3π.故选B.

答案：

B

3．（优质试题·广州综合测试

（一））如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的正视图（等腰直角三角形）和侧视图，且该几何体的体积为，则该几何体的俯视图可以是（　　）

解析：

由题意可得该几何体可能为四棱锥，如图所示，其高为2，其底面为正方形，面积为2×2＝4，因为该几何体的体积为×4×2＝，满足条件，所以俯视图可以为一个直角三角形．选D.

答案：

D

4．（优质试题·山西五校联考）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：

“今有刍甍，下广三丈，袤四丈；上袤二丈，无广；高1丈，问：

积几何？

”其意思为：

“今有底面为矩形的屋脊柱的楔体，下底面宽3丈，长4丈；上棱长2丈，高1丈，问它的体积是多少？

”已知1丈为10尺，现将该楔体的三视图给出，其中网格纸上小正方形的边长为1丈，则该楔体的体积为________立方尺．

解析：

该楔体的直观图如图中的几何体ADEBCF.取AB的中点G，CD的中点H，连接FG，GH，HF，则该几何体的体积为四棱锥FGBCH与三棱柱ADEGHF的体积之和．又可以将三棱柱ADEGHF割补成高为EF，底面积为S＝×3×1＝平方丈的一个直棱柱，故该楔体的体积V＝×2＋×2×3×1＝5立方丈＝5000立方尺．

答案：

5000