内蒙古呼和浩特市实验教育集团学年八年级上学期期中考试数Word文档格式.docx

内蒙古呼和浩特市实验教育集团学年八年级上学期期中考试数Word文档格式.docx

《内蒙古呼和浩特市实验教育集团学年八年级上学期期中考试数Word文档格式.docx》由会员分享，可在线阅读，更多相关《内蒙古呼和浩特市实验教育集团学年八年级上学期期中考试数Word文档格式.docx（28页珍藏版）》请在冰豆网上搜索。

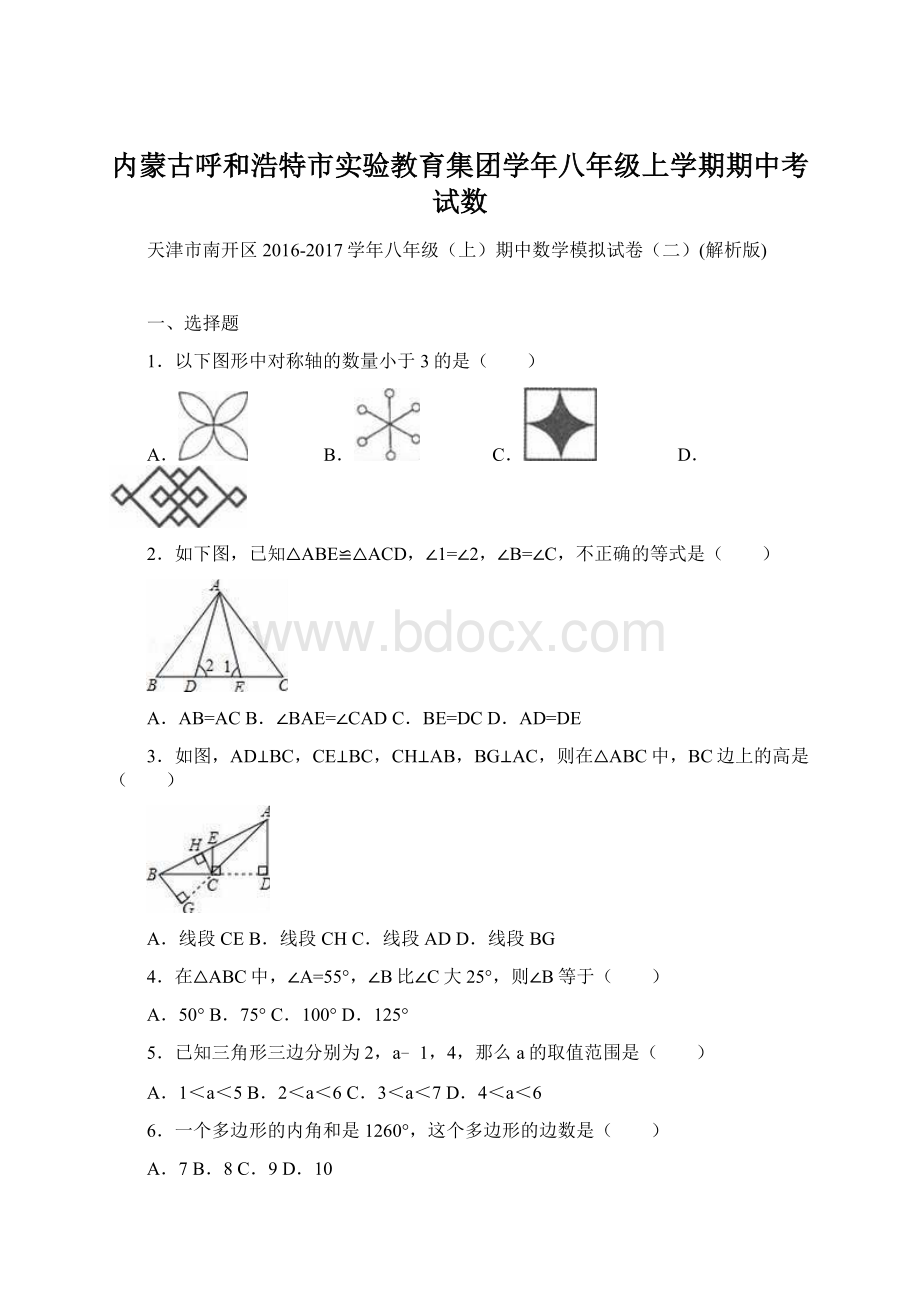
6．一个多边形的内角和是1260°

，这个多边形的边数是（　　）

A．7B．8C．9D．10

7．如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（　　）

A．1个B．2个C．3个D．4个

8．如图，AB=AC，BE⊥AC于点E，CF⊥AB于点F，BE、CF相交于点D，则①△ABE≌△ACF；

②△BDF≌△CDE；

③点D在∠BAC的平分线上．以上结论正确的是（　　）

A．①B．②C．①②D．①②③

9．如图，在Rt△ABC中，AB=AC，AD⊥BC，垂足为D．E、F分别是CD、AD上的点，且CE=AF．如果∠AED=62°

，那么∠DBF=（　　）

A．62°

B．38°

C．28°

D．26°

10．如图，等腰三角形ABC中，AB=AC，∠A=46°

，CD⊥AB于D，则∠DCB等于（　　）

A．30°

B．26°

C．23°

D．20°

11．若等腰三角形一腰上的高和另一腰的夹角为25°

，则该三角形的一个底角为（　　）

A．32.5°

B．57.5°

C．65°

或57.5°

D．32.5°

12．如图，∠MON=30°

，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，依此类推，若OA1=1，则△A2016B2016A2017的边长为（　　）

A．2016B．4032C．22016D．22015

二、填空题

13．如图，在△ABC中，点D是BC的中点，作射线AD，在线段AD及其延长线上分别取点E、F，连接CE、BF．添加一个条件，使得△BDF≌△CDE，你添加的条件是　　．（不添加辅助线）

14．如图，已知△ABC中，∠ABC=45°

，AC=4，H是高AD和BE的交点，则线段BH的长度为　　．

15．如图，∠DAB=∠EAC=60°

，AB=AD，AC=AE，BE和CD相交于O，AB和CD相交于P，则∠DOE的度数是　　°

．

16．如图所示，已知O是四边形ABCD内一点，OB=OC=OD，∠BCD=∠BAD=75°

，则∠ADO+∠ABO=　　度．

17．如图，已知△ABC中，AB=AC，∠DBC=∠D=60°

，AE平分∠BAC，若BD=8cm，DE=3cm，则BC=　　．

18．如图，在△ABC中，∠ACB=90°

，∠BAC=30°

，在直线BC或AC上取一点P，使得△PAB为等腰三角形，这样的点P共有　　个．

三、解答题（共7小题，满分66分）

19．（8分）如图，在10×

10的网格中，每个小正方形的边长都为1，网格中有两个格点A、B和直线l．

（1）求作点A关于直线l的对称点A1；

（2）P为直线l上一点，连接BP，AP，求△ABP周长的最小值．

20．（8分）在△ABC中，AB=CB，∠ABC=90°

，F为AB延长线上一点，点E在BC上，且AE=CF．

（1）求证：

△ABE≌△CBF；

（2）若∠CAE=25°

，求∠BFC度数．

21．（10分）如图，已知在△ABC中，AB=AC，AB的垂直平分线DE交AC于点E，CE的垂直平分线正好经过点B，与AC相交于点F，求∠A的度数．

22．（10分）如图，△ABC的三条内角平分线相交于点O，过点O作OE⊥BC于E点，求证：

∠BOD=∠COE．

23．（10分）如图，四边形ABDC中，∠D=∠ABD=90°

，点O为BD的中点，且OA平分∠BAC．

OC平分∠ACD；

（2）求证：

OA⊥OC；

（3）求证：

AB+CD=AC．

24．（10分）如图1，C是线段BE上一点，以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE，连结AE、BD．

BD=AE；

（2）如图2，若M、N分别是线段AE、BD上的点，且AM=BN，请判断△CMN的形状，并说明理由．

25．（10分）如图，已知等边△ABC，延长BC至D，E在AB上，使AE=CD，连接DE，交AC于F点，过E作EG⊥AC于G点．求证：

FG=AC．

2016-2017学年天津市南开区八年级（上）期中数学模拟试卷

（二）

参考答案与试题解析

【考点】轴对称图形．

【分析】根据对称轴的概念求解．

【解答】解：

A、有4条对称轴；

B、有6条对称轴；

C、有4条对称轴；

D、有2条对称轴．

故选D．

【点评】本题考查了轴对称图形，解答本题的关键是掌握对称轴的概念：

如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．

【考点】全等三角形的性质．

【分析】根据全等三角形的性质，全等三角形的对应边相等，全等三角形的对应角相等，即可进行判断．

∵△ABE≌△ACD，∠1=∠2，∠B=∠C，

∴AB=AC，∠BAE=∠CAD，BE=DC，AD=AE，

故A、B、C正确；

AD的对应边是AE而非DE，所以D错误．

【点评】本题主要考查了全等三角形的性质，根据已知的对应角正确确定对应边是解题的关键．

【考点】三角形的角平分线、中线和高．

【分析】如图，由于AD⊥BC，那么根据三角形的高的定义即可确定在△ABC中，BC边上的高．

如图，∵AD⊥BC，

∴在△ABC中，BC边上的高为线段AD．

故选C．

【点评】此题比较简单，主要考查了三角形的高的定义，利用定义即可判定AD是其高线．

【考点】三角形内角和定理．

【分析】根据三角形内角和定理计算．

设∠C=x°

，则∠B=x°

+25°

根据三角形的内角和定理得x+x+25=180﹣55，

x=50．

则x+25=75．

故选B．

【点评】能够用一个未知数表示其中的未知角，然后根据三角形的内角和定理列方程求解．

【考点】三角形三边关系；

解一元一次不等式组．

【分析】本题可根据三角形的三边关系：

两边之和大于第三边，两边之差小于第三边列出不等式：

4﹣2＜a﹣1＜4+2，化简即可得出a的取值范围．

依题意得：

4﹣2＜a﹣1＜4+2，

即：

2＜a﹣1＜6，

∴3＜a＜7．

故选：

C．

【点评】此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．

【考点】多边形内角与外角．

【分析】根据多边形的内角和公式列式求解即可．

设这个多边形的边数是n，则

（n﹣2）•180°

=1260°

，

解得n=9．

【点评】本题考查了多边形的内角和公式，熟记公式是解题的关键，是基础题，比较简单．

【考点】全等三角形的判定．

【分析】根据全等三角形的判定得出点P的位置即可．

要使△ABP与△ABC全等，点P到AB的距离应该等于点C到AB的距离，即3个单位长度，故点P的位置可以是P1，P3，P4三个，

故选C

【点评】此题考查全等三角形的判定，关键是利用全等三角形的判定进行判定点P的位置．

【考点】全等三角形的判定与性质；

角平分线的性质．

【分析】从已知条件进行分析，首先可得△ABE≌△ACF得到角相等和边相等，运用这些结论，进而得到更多的结论，最好运用排除法对各个选项进行验证从而确定最终答案．

∵BE⊥AC于E，CF⊥AB于F

∴∠AEB=∠AFC=90°

∵AB=AC，∠A=∠A，

∴△ABE≌△ACF（①正确）

∴AE=AF，

∴BF=CE，

∵BE⊥AC于E，CF⊥AB于F，∠BDF=∠CDE，

∴△BDF≌△CDE（②正确）

∴DF=DE，

连接AD，

∵AE=AF，DE=DF，AD=AD，

∴△AED≌△AFD，

∴∠FAD=∠EAD，

即点D在∠BAC的平分线上（③正确）

【点评】此题考查了角平分线的性质及全等三角形的判定方法等知识点，要求学生要灵活运用，做题时要由易到难，不重不漏．

【考点】等腰直角三角形；

全等三角形的判定与性质；

直角三角形斜边上的中线．

【分析】主要考查：

等腰三角形的三线合一，直角三角形的性质．注意：

根据斜边和直角边对应相等可以证明△BDF≌△ADE．

∵AB=AC，AD⊥BC，

∴BD=CD．

又∵∠BAC=90°

∴BD=AD=CD．

又∵CE=AF，

∴DF=DE．

∴Rt△BDF≌Rt△ADE（SAS）．

∴∠DBF=∠DAE=90°

﹣62°

=28°

【点评】熟练运用等腰直角三角形三线合一性质、直角三角形斜边上的中线等于斜边的一半．

【考点】等腰三角形的性质；

直角三角形的性质．

【分析】先根据等腰三角形的性质和三角形内角和定理求出∠B的度数，进而在Rt△DCB中，求得∠DCB的度数．

∵∠A=46°

，AB=AC，

∴∠