 套卷江苏省南通市届高三第一次调研测试数学试题Word格式.docx
套卷江苏省南通市届高三第一次调研测试数学试题Word格式.docx
- 文档编号:13507964
- 上传时间:2022-10-11
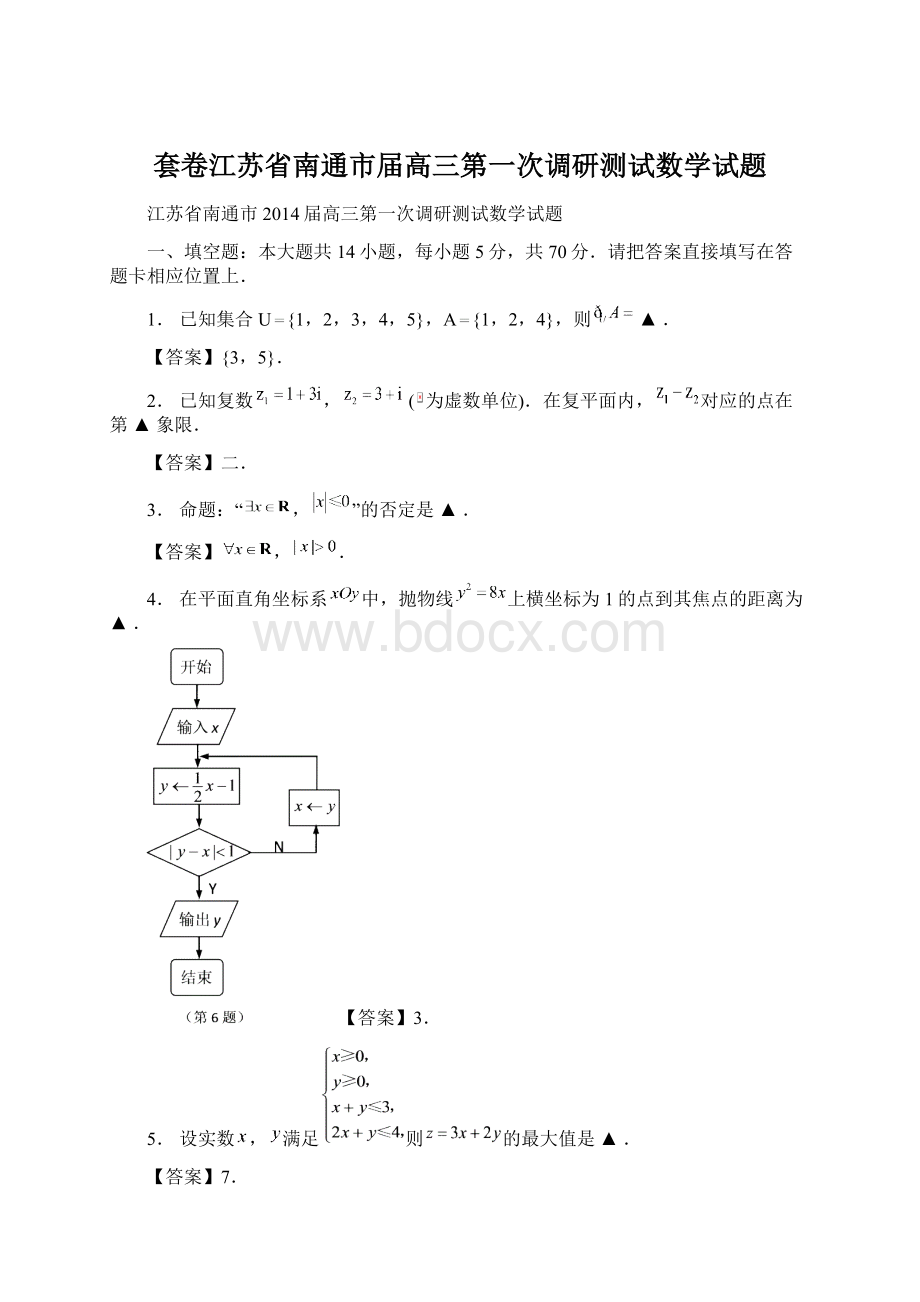
- 格式:DOCX
- 页数:14
- 大小:334.99KB
套卷江苏省南通市届高三第一次调研测试数学试题Word格式.docx
《套卷江苏省南通市届高三第一次调研测试数学试题Word格式.docx》由会员分享,可在线阅读,更多相关《套卷江苏省南通市届高三第一次调研测试数学试题Word格式.docx(14页珍藏版)》请在冰豆网上搜索。
第1天
第2天
第3天
第4天
第5天
甲
109
111
132
118
110
乙
115
112
则空气质量指数(AQI)较为稳定(方差较小)的城市为▲(填甲或乙).
【答案】乙.
8.已知正三棱锥的侧棱长为1,底面正三角形的边长为.现从该正三棱锥的六条棱中随机选取两条棱,则这两条棱互相垂直的概率是▲.
9.将函数的图象上所有点向右平移个单位后得到的图象关于原点对称,则等于▲.
10.等比数列{an}的首项为2,公比为3,前n项和为Sn.若log3[an(S4m+1)]=9,则+的最小值
是▲.
11.若向量,,且,则的值是▲.
【答案】1.
12.在平面直角坐标系中,直线是曲线的切线,则当>0时,实数的最小值是▲.
13.已知集合M=≤y≤,N=≥,则表示M∩N的图形面积等于▲.
14.若函数对任意实数,在闭区间上总存在两实数、,使得8成立,则实数的最小值为▲.
【答案】8.
二、解答题:
本大题共6小题,共90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
如图,在四棱柱中,,,且.
(1)求证:
∥平面;
(2)求证:
⊥平面.
(1)证明:
在四棱柱中,,
平面,
所以平面.……………………………………………………………………6分
(2)证明:
在四棱柱中,四边形为平行四边形,又,
故四边形为菱形.
从而.……………………………………………………………………………9分
又,而,平面,
所以平面.…………………………………………………………………14分
16.(本小题满分14分)
在△ABC中,a,b,c分别为角A,B,C所对的边长,且c=-3bcosA,tanC=.
(1)求tanB的值;
(2)若,求△ABC的面积.
(1)解:
由正弦定理,得,………………………………………………2分
即.
所以.
从而.
因为,所以.……………………………………………………4分
又,由
(1)知,,
解得.………………………………………………………………………………6分
(2)解:
由
(1),得,,.………………………………10分
由正弦定理,得.……………………………………………12分
所以△ABC的面积为.………………………………14分
17.(本小题满分14分)
已知a为实常数,y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<
0时,f(x)=2x-+1.
(1)求函数f(x)的单调区间;
(2)若f(x)≥a-1对一切x>0成立,求a的取值范围.
由奇函数的对称性可知,我们只要讨论f(x)在区间(-∞,0)的单调性即可.
f′(x)=2+,令f′(x)=0,得x=-a.…………………………………………………2分
①当a≤0时,f′(x)>0,故f(x)在区间(-∞,0)是单调递增.………………………4分
②当a>0时,x∈(-∞,-a),f′(x)>0,所以f(x)在区间(-∞,-a)是单调递增.
x∈(-a,0),f′(x)<0,所以f(x)在区间(-a,0)是单调减.………………………6分
综上所述:
当a≤0时,f(x)单调增区间为(-∞,0),(0,+∞);
当a>0时,f(x)单调增区间为(-∞,-a),(a,+∞),单调减区间为(-a,0),(0,a).……………………7分
因为f(x)为奇函数,
所以当x>0时,f(x)=-f(-x)=-(-2x-+1)=2x+-1.……………………9分
①当a<0时,要使f(x)≥a-1对一切x>0成立,即2x+≥a对一切x>0成立.
而当x=->0时,有-a+4a≥a,所以a≥0,则与a<0矛盾.
所以a<0不成立.………………………………………………………………………11分
②当a=0时,f(x)=2x-1>-1=a-1对一切x>0成立,故a=0满足题设要求.…12分
③当a>0时,由
(1)可知f(x)在(0,a)是减函数,在(a,+∞)是增函数.
所以fmin(x)=f(a)=3a-1>a-1,所以a>0时也满足题设要求.…………………13分
综上所述,a的取值范围是.……………………………………………………14分
18.(本小题满分16分)
如图,一块弓形薄铁片EMF,点M为的中点,其所在圆O的半径为4dm(圆心O在弓形EMF内),∠EOF=.将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗),AD∥EF,且点A、D在上,设∠AOD=.
(1)求矩形铁片ABCD的面积S关于的函数关系式;
(2)当矩形铁片ABCD的面积最大时,求cos的值.
设矩形铁片的面积为,.
当时(如图①),,,
.……………………………3分
当时(如图②),,,
故.
综上得,矩形铁片的面积S关于的函数关系式为
………………………………………………………7分
当时,求导,得
.
令,得.……………………………………………………………10分
记区间内余弦值等于的角为(唯一存在).列表:
增函数
极大值
减函数
又当时,在上的单调减函数,
所以当即时,矩形的面积最大.…………………………………16分
19.(本小题满分16分)
如图,在平面直角坐标系中,椭圆过点,离心率为,又椭圆内接四边形ABCD(点A、B、C、D在椭圆上)的对角线AC,BD相交于点,且,.
(1)求椭圆的方程;
(2)求直线AB的斜率.
依题意,解得
所求椭圆的方程为.…………………………………………………………6分
设,则.
由,得.……………………………………………………8分
代入椭圆方程,得.
整理,得,…………………………………………………10分
即.③……………………………………………12分
设,同理可得.④……………………………………………14分
③④,得,即直线AB的斜率为.……………………16分
20.(本小题满分16分)
已知等差数列{an}、等比数列{bn}满足a1+a2=a3,b1b2=b3,且a3,a2+b1,a1+b2成等差数列,a1,a2,b2成等比数列.
(1)求数列{an}和数列{bn}的通项公式;
(2)按如下方法从数列{an}和数列{bn}中取项:
第1次从数列{an}中取a1,
第2次从数列{bn}中取b1,b2,
第3次从数列{an}中取a2,a3,a4,
第4次从数列{bn}中取b3,b4,b5,b6,
……
第2n-1次从数列{an}中继续依次取2n-1个项,
第2n次从数列{bn}中继续依次取2n个项,
由此构造数列{cn}:
a1,b1,b2,a2,a3,a4,b3,b4,b5,b6,a5,a6,a7,a8,a9,b7,b8,b9,b10,b11,b12,…,记数列{cn}的前n和为Sn.求满足Sn<22014的最大正整数n.
设等差数列{an}的公差为,等比数列{bn}的公比为,
依题意,得解得a1=d=1,b1=q=2.
故an=n,bn=2n.……………………………………………………………………………6分
将a1,b1,b2记为第1组,a2,a3,a4,b3,b4,b5,b6记为第2组,a5,a6,a7,a8,a9,b7,b8,b9,b10,b11,b12记为第3组,……以此类推,则第n组中,有2n-1项选取于数列{an},有2n项选取于数列{bn},前n组共有n2项选取于数列{an},有n2+n项选取于数列{bn},记它们的总和为Pn,并且有.…………11分
,
当+(2+22+…+22012)时,
.…………………………………………………13分
当+(2+22+…+22013)时,
可得到符合的最大的n=452+2012=4037.……………………………………16分
数学Ⅱ(附加题)参考答案与评分标准
21.【选做题】
A.选修4—1:
几何证明选讲
(本小题满分10分)
在△ABC中,已知CM是∠ACB的平分线,△AMC的外接圆交BC于点N,且BN2AM.
求证:
ABAC.
证明:
如图,在△ABC中,因为CM是∠ACM的平分线,
所以①……………………………3分
又因为BA与BC是圆O过同一点B的割线,
所以,
即……………………………………6分
又BN=2AM,
所以②……………………………8分
由①②,得ABAC.………………………10分
B.选修4—2:
矩阵与变换
设二阶矩阵,满足,,求.
解:
设,因为,…………………………………………………2分
所以,即……………………………………………6分
解得所以.……………………………………………………10分
C.选修4—4:
坐标系与参数方程
在极坐标系中,已知曲线:
,过极点O的直线与曲线相交于A、B两点,
,求直线的方程.
解:
设直线的方程为(ρ∈R),,,…………………………………2分
则.…………………………………………………………………5分
又,故.……………………………………………………………7分
解得+2kπ或+2kπ,k∈Z.
所以直线的方程为或(ρ∈R).…………………………………………10分
D.选修4—5:
不等式选讲
已知x,y,z均为正数,求证:
证明:
因为x,y,z均为正数,所以.………………………………4分
同理可得,.…………………………………………………7分
当且仅当xyz均时,以上三式等号都成立.
将上述三个不等式两边左,右两边分别相加,并除以2,
得.……………………………………………………………10分
【必做题】
22.(本小题满分10分)
如图,设,,…,为单位圆上逆时针均匀分布的六个点.现任选其中三个不同点构成一
个三角形,记该三角形的面积为随机变量.
(1)求的概率;
(2)求的分布列及数学期望.
(1)从六个点任选三个不同点构成一个三角形共
有种不同选法,其中的为有一个角是
的直角三角形(如△),共种,
所以.…………
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 江苏省 南通市 届高三 第一次 调研 测试 数学试题
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 (完整word版)信息论与编码期末考试题----学生复习用.doc
(完整word版)信息论与编码期末考试题----学生复习用.doc
 (完整版)固定资产盘点表.xls
(完整版)固定资产盘点表.xls
