结构力学讲义DOCWord格式文档下载.docx

结构力学讲义DOCWord格式文档下载.docx

《结构力学讲义DOCWord格式文档下载.docx》由会员分享，可在线阅读，更多相关《结构力学讲义DOCWord格式文档下载.docx（76页珍藏版）》请在冰豆网上搜索。

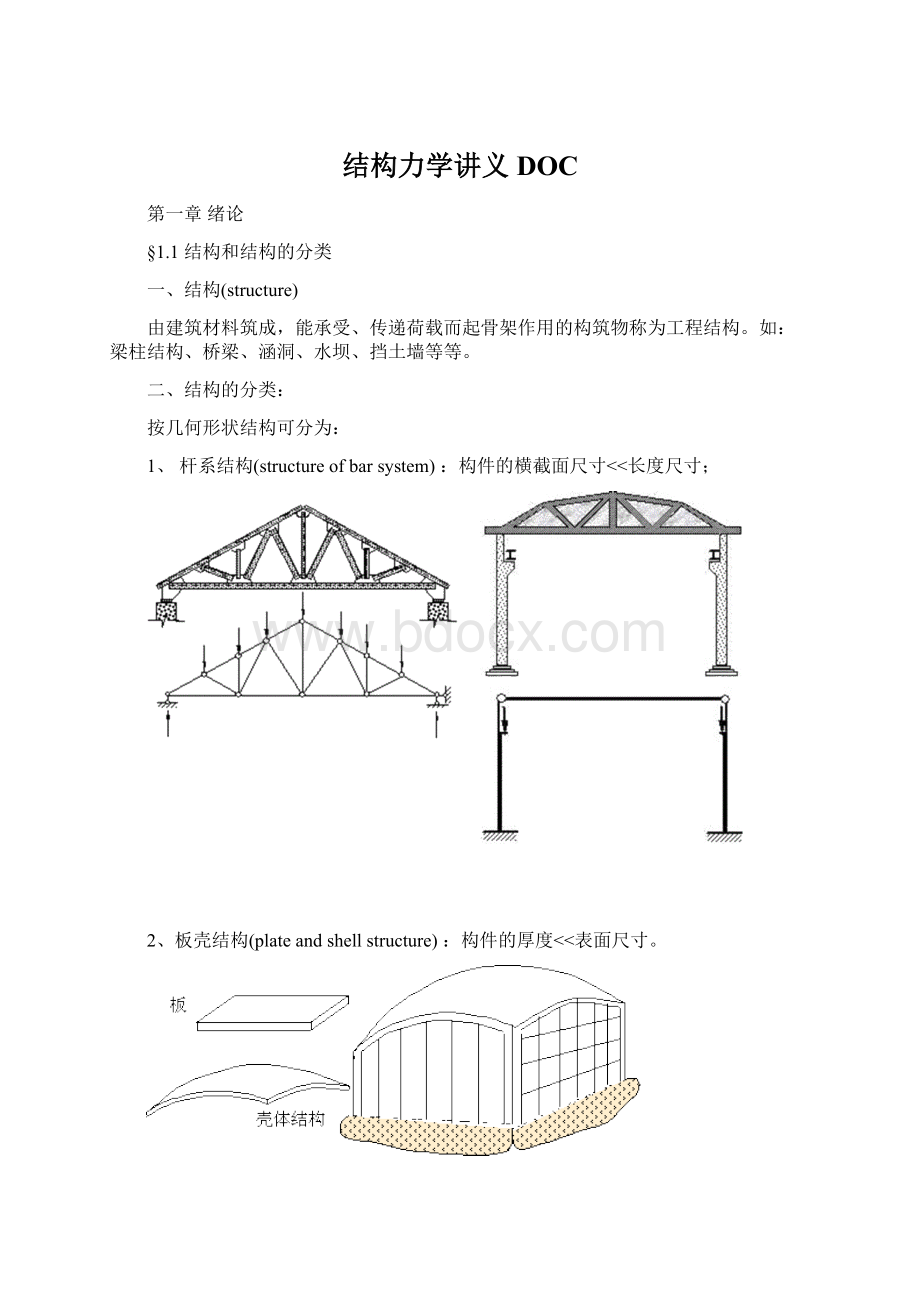
1.2结构力学的研究对象、任务和方法

一、各力学课程的比较：

二、结构力学的任务：

1、研究荷载等因素在结构中所产生的内力（强度计算）；

2、计算荷载等因素所产生的变形（刚度计算）；

3、分析结构的稳定性（稳定性计算）；

4、探讨结构的组成规律及合理形式。

进行强度、稳定性计算的目的，在于保证结构满足安全和经济的要求。

计算刚度的目的，在于保证结构不至于发生过大的变形，以至于影响正常使用。

研究组成规律目的，在于保证结构各部分，不至于发生相对的刚体运动，而能承受荷载维持平衡。

探讨结构合理的形式，是为了有效地利用材料，使其性能得到充分发挥。

三、研究方法：

在小变形、材料满足虎克定律的假设下综合考虑：

1、静力平衡；

2、几何连续；

3、物理关系三方面的条件，建立各种计算方法。

1.3结构的计算简图（computingmodelofstructure）

一、选取结构的计算简图必要性、重要性：

将实际结构作适当地简化，忽略次要因素，显示其基本的特点。

这种代替实际结构的简化图形，称为结构的计算简图。

合理地选取结构的计算简图是结构计算中的一项极其重要而又必须首先解决的问题。

二、选取结构的计算简图的原则：

1、能反映结构的实际受力特点，使计算结果接近实际情况。

2、忽略次要因素，便于分析计算。

三、影响计算简图选取的主要因素：

1、结构的重要性：

重要结构——精；

次要结构——粗；

2、设计阶段：

初步设计——粗；

技术设计——精；

3、计算问题的性质：

静力计算——精；

动力计算——粗；

4、计算工具：

先进——精；

简陋——粗

四、结构简化的几个主要方面：

1、结构体系的简化：

一般结构实际上都是空间结构，各部相连成为一空间整体，以承受各方向可能出现的荷载。

在多数情况下，常忽略一些次要的空间约束，而将实际结构分解为平面结构。

2、杆件的简化

杆件用其轴线表示，杆件之间的连接区用结点表示，杆长用结点间距表示，荷载作用于轴线上。

3、杆件间的连接区通常简化成为三种理想情况：

1）铰结点：

约束各杆端不能相对移动，但可相对转动；

可以传递力，不能传递力矩。

2）刚结点：

连接各杆端既不能相对移动，又不能相对转动；

既可以传递力，又可传递力矩。

3）组合结点：

是一些杆端为刚结，另一些杆端为铰结。

4、支座的简化

1）滚轴支座：

约束杆端不能竖向移动，但可水平移动和转动。

只有竖向反力。

2）定向支座：

允许杆端沿一定方向自由移动，而沿其它方向不能移动，也不能转动。

3）固定支座（fixedsupport）：

约束杆端不能移动也不能转动，有三个反力分量。

4）铰支座（hingesupport）：

约束杆端不能移动，但可以转动。

有两个互相垂直的反力，或合成为一个合力。

5、材料的性质的简化：

理想弹性材料。

6、荷载的简化

体力和面力均简化为作用在轴线上的分布荷载和集中荷载。

第二章几何组成分析

2.1体系的分类 

一、几何构造分析（geometricconstructionanalysis）的目的

1、研究结构正确的连接方式，确保所设计的结构能承受并传递荷载，维持平衡，不至于发生刚体运动。

2、在结构计算时，可根据其几何组成情况，选择适当的计算方法；

分析其组成顺序，寻找简便的解题途径。

在忽略变形的前提下，体系可分为两类：

1、几何不变体系（geometricallyunchangeablesystem）：

在任何外力作用下，其形状和位置都不会改变。

2、几何可变体系（geometricallyunchangeablesystem）：

在外力作用下，其形状或位置会改变。

几何可变体系又可分为两种：

几何常变体系：

受力后可发生有限位移。

几何瞬变体系：

受力后可发生微量位移

二、建筑结构只能是几何不变体系

几何常变体系受力后会发生刚体运动，瞬变体系能产生很大的内力（或不确定），故几何瞬变体系不能作为建筑结构使用。

只有几何不变体系才能作为建筑结构使用。

2.2约束

约束（restraint）在体系内部加入的减少自由度的装置。

1、链杆：

仅在两处与其它物体用铰相连，不论其形状和铰的位置如何。

一根链杆可以减少体系一个自由度，相当于一个约束。

2、铰：

联结两个刚片的铰。

单铰可减少体系两个自由度相当于两个约束。

联结两刚片的两根不共线的链杆相当于一个单铰即瞬铰。

3、铰（复铰）：

联结三个或三个以上刚片的铰。

联结n个刚片的复铰相当于n-1个单铰，相当于2（n-1）个约束。

4、多余约束（redundantrestraint）：

不减少体系自由度的约束称为多余约束。

2.3自由度

一、自由度（degreeoffreedom）

所谓体系的自由度是指体系运动时，可以独立改变的几何参数的数目；

即确定体系位置所需独立坐标的数目。

1、平面内一点2个自由度；

2、平面内一刚片3个自由度。

二、体系的计算自由度 

一个平面体系通常都是由若干部件（刚片或结点）加入一些约束组成。

按照各部件都是自由的情况，算出各部件自由度总数，再算出所加入的约束总数，将两者的差值定义为：

体系的计算自由度（computationaldegreeoffreedom）W。

即：

W=（各部件自由度总数）－（全部约束总数）

如刚片数m，单刚接数g，单铰数n，支承链杆数r，则：

W=3m－（3g+2n+r）

注意：

1、复连接要换算成单连接。

2、刚接在一起的各刚片作为一大刚片。

如带有a个无铰封闭框，约束数应加3a个。

3、铰支座、定向支座相当于两个支承链杆，固定端相三于个支承链杆。

4、对于铰接链杆体系也可将结点视为部件，链杆视为约束，则：

W=2j－b－r

式中：

j为结点数；

b为链杆数；

r支承链杆数。

例1求右图体系的计算自由度

m=1，链杆b＝4，铰结h＝0，刚结g＝3

W=3×

1-（3×

3+2×

0+4×

1）=3-13=-10

例2求右图体系的计算自由度

解：

刚片m＝7，D、E为复杂铰，因此简单铰h＝9，支杆数b＝3，刚结=0，故：

W=37-29-31=0。

1、W并不一定代表体系的实际自由度，仅说明了体系必须的约束数够不够。

即：

W>

0体系缺少足够的约束，一定是几何可变体系。

W=0实际约束数等于体系必须的约束数,但不能判定体系是否几何不变。

。

W<

0体系有多余约束，但不能判定体系是否几何不变。

由此可见:

W≤0只是保证体系为几何不变的必要条件,而不是充分条件。

2、实际自由度S、计算自由度W和多余约束n之间的关系：

S=（各部件自由度总数）－（非多余约束数）=（各部件自由度总数）－（全部约束数－多余约束数）

=（各部件自由度总数）－（全部约束数）+（多余约束数）

S=W-n

由此可见：

只有当体系上没有多余约束时，计算自由度才是体系的实际自由度

2.4无多余约束几何不变体系的组成规则 

三角形的三个边给定，三角形的形状唯一确定。

故铰结三角形是一个几何形状不便的体系。

将三角形中的链杆视为刚片，可得到由刚片组成几何不变体系的组成规则。

规则一、三刚片以不在一条直线上的三铰相联，组成无多余约束的几何不变体系。

规则二、两刚片以一铰及不通过该铰的一根链杆相联组成无多余约束的几何不变体系。

规则三、两刚片以不互相平行，也不相交于一点的三根链杆相联，组成无多余约束的几何不变体系。

规则四、一点与一刚片用两根不共线的链杆相联，组成无多余约束的几何不变体系。

如果规则中的要求得不到满足，将组成几何常变体系或几何瞬变体系。

2.5几何组成分析举例

几种常见的分析途径 

，利用上述的基本规则就可以对体系进行几何部变形的分析。

要理解规则，灵活应用。

例3：

分析右图所示体系的几何构造

（i）刚片I与II由铰C联结

（ii）刚片I与基础III由链杆1、2联结，相当有一个瞬铰在A点。

（iii）刚片II与基础III由链杆3、4联结，相当有一个瞬铰在B点。

如果：

A、B、C三点不在同一直线上，则：

体系是几何不变的；

若：

A、B、C三点在同一直线上，则：

体系是几何瞬变的；

变化后，三点不共线，故为几何不变体。

需要注意的几个问题：

（1）去掉二元体，将体系化简单，然后再分析。

（2）如上部体系于基础用满足要求三个约束相联可去掉基础，只分析上部。

（3）当体系杆件数较多时，将刚片选得分散些，刚片与刚片之间用链杆形成的瞬铰相连，而不用单铰相连。

（4）由一基本刚片开始，逐步增加二元体，扩大刚片的范围，将体系归结为两个刚片或三个刚片相连，再用规则判定。

（5）由基础开始逐件组装。

（6）刚片的等效代换：

在不改变刚片与周围的连结方式的前提下，可以改变它的大小、形状及内部组成。

2.6体系的几何组成与静力特性的关系

1、静定结构：

在几何组成上是几何不变、无多余约束的体系，其全部支反力和内力均可由静力平衡条件唯一确定。

2、超静定结构：

在几何组成上是几何不变、有多余约束的体系，其全部支反力和内力均不可由静力平衡条件唯一确定，还须补充其他条件。

第三章静定结构的受力分析

3.1梁的内力计算回顾

一、截面法

1、平面杆件的截面内力分量及正负规定：

轴力N（normalforce）截面上应力沿轴线切向的合力以拉力为正。

剪力Q（shearingforce）截面上应力沿轴线法向的合力以绕隔离体顺时针转为正。

弯矩M（bendingmoment）截面上应力对截面中性轴的力矩。

不规定正负，但弯矩图画在受拉侧。

2、截面内力计算的基本方法：

截面法：

截开、代替、平衡。

内力的直接算式：

直接由截面一边的外力求出内力。

1、轴力=截面一边的所有外力沿轴切向投影代数和。

2、剪力=截面一边的所有外力沿轴法向投影代数和，如外力绕截面形心顺时针转动，投影取正否则取负。

3、弯矩=截面一边的所有外力对截面形心的外力矩之和。

弯矩及外力矩产生相同的受拉边。

二、内力图的形状特征

内力图与荷载的对应关系

内力图与支承、连接之间的对应关系

1、在自由端、铰结点、铰支座处的截面上无集中力偶作用时，该截面弯矩等于零（如图1-（a）C右截面、图1-（b）A截面），有集中力偶作用时，该截面弯矩等于这个集中力偶，受拉侧可由力偶的转向直接确定（如图1-（a）C左截面和D截面）。

2、在刚结点上，不仅要满足力的投影平衡，各杆端弯矩还要满力矩平衡条件∑M=0。

尤其是两杆相交刚结点上无外力偶作用时，两杆端弯矩等值，同