文科数学全国三卷真题及答案Word文档格式.docx

文科数学全国三卷真题及答案Word文档格式.docx

《文科数学全国三卷真题及答案Word文档格式.docx》由会员分享，可在线阅读，更多相关《文科数学全国三卷真题及答案Word文档格式.docx（16页珍藏版）》请在冰豆网上搜索。

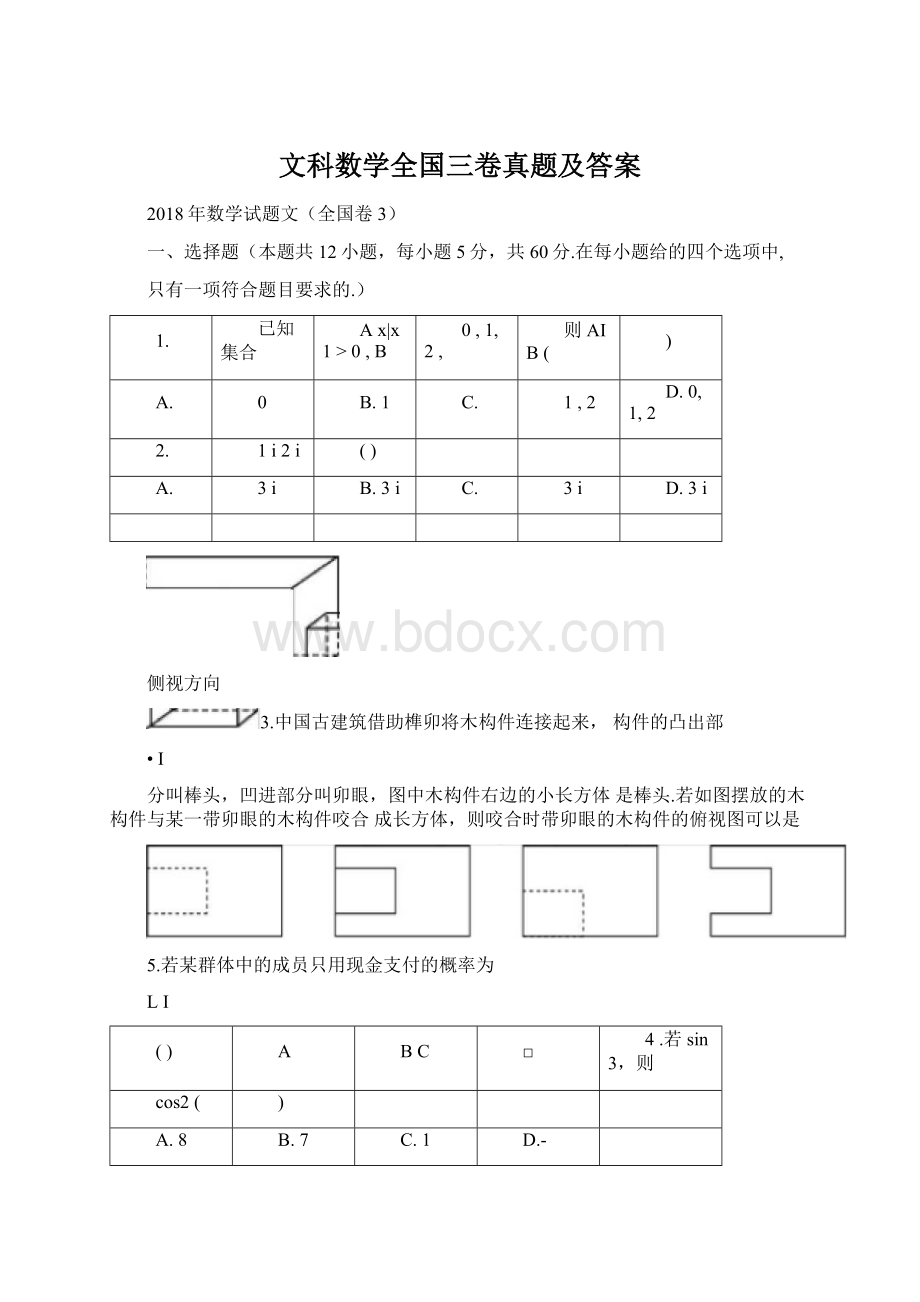
C.1

D.-

9

0.45,既用现金支付也用非现金支付的

概率为0.15，则不用现金支付的概率为（）

A.0.3B.0.4C.0.6D.0.7

6.函数fx丄畔的最小正周期为（）

1tanx

-

B.-

C.D.

2

4

7.

下列函数中，

其图像与函数

yInX的图像关于直线

x1对称的是（

yIn1x

B.yIn2

xC.yIn1x

D.yIn2x

面积的取值范围是（

角形且其面积为93，则三棱锥DABC体积的最大值为（

二、填空题（本题共4小题，每小题5分，共20分）13.已知向量a=1,2,b=2,2,c=1，入.若c//2a+b，则

4某公司有大量客户，且不同年龄段客户对其服务的评价有较大差异.为了解客

户的评价，该公司准

备进行抽样调查，可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样，则

最合适的抽样方法是

fy的最大值是

2xy3>

0,

5若变量x,y满足约束条件x2y4>

0,则z

x2w0.

三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤，第17~31题为

必考题，每个试

考生都必须作答，第22、23题为选考题，考生根据要求作答.）

（一）必考题：

共60分。

17.（12分）

等比数列an中，a1,a54a3.

⑴求an的通项公式；

⑵记Sn为an的前n项和.若Sm63，求m.

18.（12分）

某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的

生产方式.为比较两

种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，

第二组工人用第二种生产方式.根据工人完成生产任务的工作时间（单位：

min）绘

制了如下茎叶图：

⑴根据茎叶图判断哪种生产方式的效率更高？

并说明理由；

⑵求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表：

超过m

不超过m

一种生产方式

第二种生

产方式

⑶根据⑵中的列表，能否有99%勺把握认为两种生产方式的效率有差异?

nadbe

PK>

k

0.0500.0100.001

abedaebd'

k

3.8416.63510.828

附：

K2

19.（12分）

III

如图，矩形ABCD所在平面与半圆弧二所在平面垂直，M是二上异于C,D的点.

⑴证明：

平面AMD丄平面BMC；

⑵在线段AM上是否存在点P，使得MC//平面PBD?

说明理由.

0（12分）

22已知斜率为的直线I与椭圆C:

xy1交于A,B两点.线段AB的中点为

43

1,mm0.

jI

⑴证明:

k1;

2，

⑵设为C的右焦点，P为C上一点，且FPFAFB0.证明：

2岡|FA||FB.

1（12分）

2彳已知函数X.

e

⑴求由线fx在点0,1处的切线方程；

⑵证明：

当>

1时，fxe>

0.

（二）选考题：

共10分，请考生在第22、23题中任选一题作答。

如果多做，则按

所做的第一题计分.

I.,I

2［选修4—4:

坐标系与参数方程］（10分）

在平面直角坐标系xOy中，OO的参数方程为Xcos

精心整理

⑵求AB中点P的轨迹的参数方程.

23.［选修4—5:

不等式选讲］（10分）

设函数fx2x1x1.

⑴画出yfx的图像；

⑵当x€0,,fxwaxb,

求ab的最小值.

参考答案

一、选择题

1.答案：

C

解答：

•••A{x|x10}{x|x1},B

{0,1,2}，二AIB{1,2}.故选C.

2.答案：

D

（1i）（2i）2ii23i，选D.

3.答案：

根据题意，A选项符号题意；

4.答案：

B

cos2-12sin21■-—.故选B.

99

5.答案：

由题意P10.450.150.4.故选B.

6.答案：

解答:

sinx

二f（X）的周期T2.故选C.

7.答案：

f（x）关于x1对称,

则f（x）f（2x）ln（2x）.故选B.

8答案：

由直线xy

20得A（2,0）,B（0,2），二|AB|.222222，圆

9.答案：

结合图象，可知D选项正确.

10.答案：

由题意eC2，则b1,故渐近线方程为xy0，则点（4,0）到渐

aa

近线的距离为d〔4「0|2^2.故选D.

11.答案：

•••C7.故选C.

12.答案：

如图，ABC为等边三角形，点O为A,B,C,D外接球的球心，G为ABC的重心，由Sabc9,3，得AB6，取BC的中点H，二AHABsin6033，二AG-AH2、、3,

3

二球心O到面ABC的距离为d?

42（2「3）22，二三棱锥DABC体积最大值

Vdabc19.3（24）18.3.

二、填空题

13.答案：

1

2：

b（4,2）,V»

/（2；

b），二1240，解得1.

14.答案：

分层抽样

由题意，不同龄段客户对其服务的评价有较大差异，故采取分层抽样法.

15.答案：

由图可知在直线x2y40和x2的交点（2,3）处取得最大值，故z2133.

16.答案：

fxIn•1x2x1（xR）

f（x）f（x）ln（~x）1In&

1x2x）1ln（1x2x2）22,

f（a）f（a）2，二f（a）2.

三、解答题

17.答案：

（1）an2n1或an

（2）n1;

（2）6.

（1）设数列｛an｝的公比为q，二q2竺4，二q2.a3

…an

2n

1或an

（2）n1

.

（2）

由

（1）知，Sn

12n

1

（2）n1n

1或Sn[1

（2）],

12

123

.Sm

?

m

163或Sm

1[1（

2）m]

63（舍）,

/.m

6.

18.

（1）第一种生产方式的平均数为*84，第二种生产方式平均数为

X274.7.

>

••

Nx2,所以第一种生产方式完成任务的平均时间大于第二种，二第二

种生产方式的效率更高

（2）由茎叶图数据得到m80•.列联表为

的把握认为两种生产方式的效率有差异19.

（1）V正方形ABCD半圆面CMD,

.AD半圆面CMD，二AD平面MCD.

•/CM在平面MCD内，.ADCM，又TM是半圆弧CD上异于C,D的点，.CMMD.又TADIDMD，二CM平面ADM,TCM在平面BCM内，.••平面BCM平面ADM.

（2）线段AM上存在点P且P为AM中点，证明如下:

连接BD,AC交于点0,连接PD,PB,PO;

在矩形ABCD中,

O是AC中点,

P是AM的中点;

/.OP//MC，丁0P在平面PDB内，MC不在平面PDB内,

•MC//平面

PDB.

20.

（1）设直线l方程为ykxt，设A%,yi）,BEy2）,

ykxt

x23y2联立消y得（4k23）x28ktx

———1

4t2

120,

贝S64k2t24（4t212）（34k2）0,

得4k23t2…①，

8ktc22,34k2

X2

y1y2

k（xi

X2）

2t

6t22m,

4k2

0，二t0且k

0.

由①②得4k2

（34k2）2

16k2，

•/k

uir

FP

2.

uuuirruir

FAFB0,FP

uuu2FM

0,

Vm（1m）,

F（1,0），二P的坐标为

（1,2m）.

由于p在椭圆上」4

M（1,号）,

22

又乞丘1,

X2_y_

f（x）

g（x）

两式相减可得生丄

X1X2

^又x1x22,y1

直线l方程为y

y

x

7

x4，

x—

2，

L1

y2

（X

3x（x2

4y1y2'

1）,

消去y得28x256x10,

uuruir■

|FA||FB|_（X11）2

|FP|

（11）2

x1,2

143、、21

14，

y1

y223,

uuu

.|FA|

|FB|

32

（0）

2|FP|.

21.

（1）由题意:

（ex）2"

.f（0）22，即曲线y

（2ax1）ex（ax2x1）ex

（1）2（x0），即2x

（2）证明：

由题意:

ex1ax2x1,

x1

…g（x）e2ax1,

axx

ax22axx2

x>

x在点o,

原不等式等价于:

g（x）e

）上单调递增，二g（x）在（

xo1

12ax010，即exo12ax01,

上单调递增，g（x）g（Xo）.

处的切线斜率为2,

x12

eax

x1o恒成立；

令

（x）0恒成立，二g