完整word《锐角的三角比》全章复习与巩固提高知识讲解Word文件下载.docx

完整word《锐角的三角比》全章复习与巩固提高知识讲解Word文件下载.docx

《完整word《锐角的三角比》全章复习与巩固提高知识讲解Word文件下载.docx》由会员分享，可在线阅读，更多相关《完整word《锐角的三角比》全章复习与巩固提高知识讲解Word文件下载.docx（19页珍藏版）》请在冰豆网上搜索。

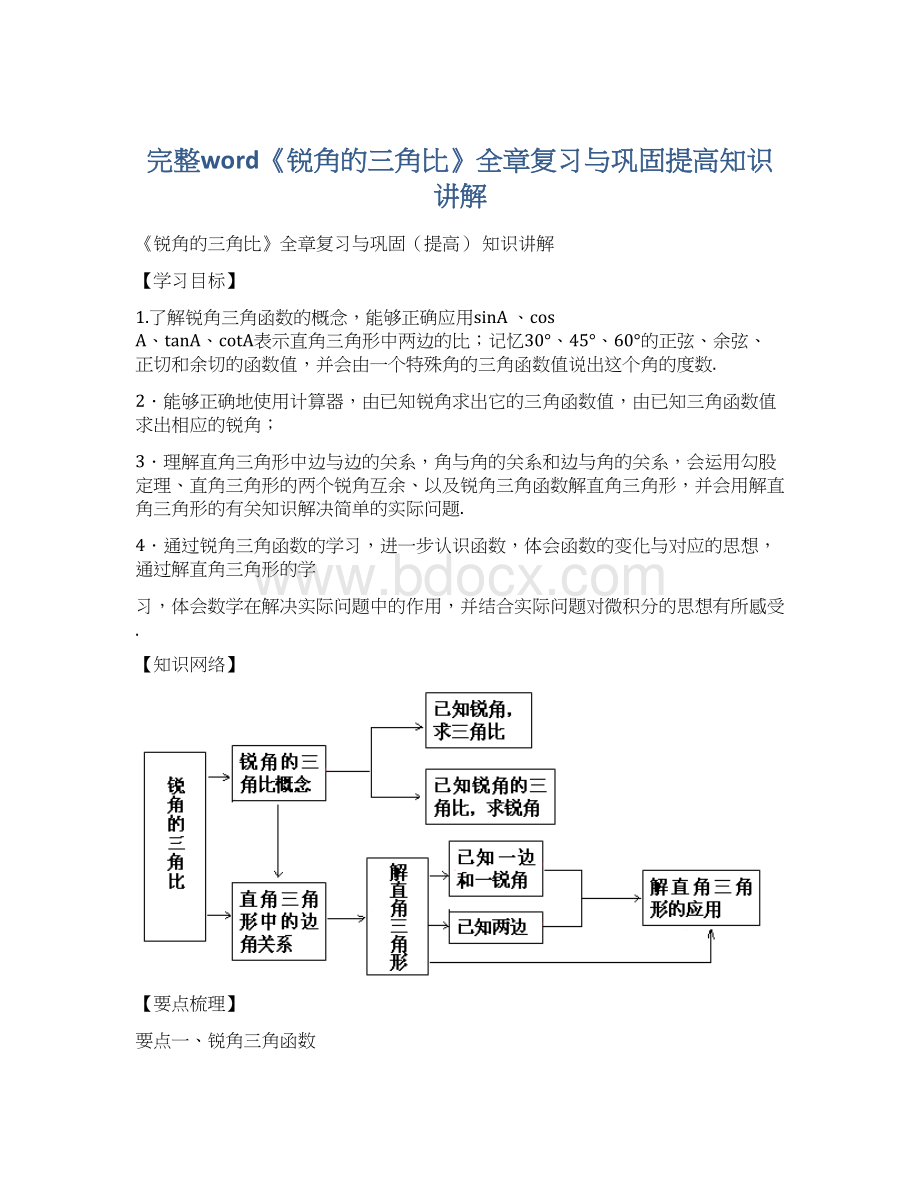
A，对于用三个大写字母表示一个角时，其三角函数中符号“∠”不能省略，应写成sin∠BAC，而不能写出sinBAC.

　　（3）sin2A表示（sinA）2，而不能写成sinA2.

　　（4）三角函数有时还可以表示成

等.

2.锐角三角函数的定义

　　锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

　　1.函数值的取值范围

对于锐角A的每一个确定的值，sinA有唯一确定的值与它对应，所以sinA是∠A的函数.同样，cosA、tanA、cotA也是∠A的函数，其中∠A是自变量，sinA、cosA、tanA、cotA分别是对应的函数.其中自变量∠A的取值范围是0°

＜∠A＜90°

，函数值的取值范围是0＜sinA＜1，0＜cosA＜1，tanA＞0，cotA>

0.

　　2．锐角三角函数之间的关系：

　　余角三角函数关系：

“正余互化公式”如∠A+∠B=90°

，

那么：

sinA=cosB；

cosA=sinB；

tanA=cotB,cotA=tanB.

　　同角三角函数关系：

sin2A＋cos2A=1；

　　3.30°

角的三角函数值

∠A

30°

45°

60°

sinA

cosA

tanA

1

cotA

　　30°

角的三角函数值和解30°

直角三角形和解45°

直角三角形为本章重中之重，是几何计算题的基本工具，三边的比借助锐角三角函数值记熟练.

要点二、解直角三角形

　　在直角三角形中，由已知元素求出未知元素的过程，叫做解直角三角形．

　　解直角三角形的依据是直角三角形中各元素之间的一些相等关系，如图：

　　角角关系：

两锐角互余，即∠A+∠B=90°

；

　　边边关系：

勾股定理，即

　　边角关系：

锐角三角函数，即

　　解直角三角形，可能出现的情况归纳起来只有下列两种情形：

（1）已知两条边（一直角边和一斜边；

两直角边）；

（2）已知一条边和一个锐角（一直角边和一锐角；

斜边和一锐角）．这两种情形的共同之处：

有一条边．因此，直角三角形可解的条件是：

至少已知一条边．

要点三、解直角三角形的应用

　　解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.

1.解这类问题的一般过程

（1）弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.

（2）将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.

　　（3）根据直角三角形（或通过作垂线构造直角三角形）元素（边、角）之间的关系解有关的直角三角形.

　　（4）得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.

　　2.常见的应用问题

（1）坡度：

坡角:

.

（2）方位角：

　　（3）仰角与俯角：

1．解直角三角形的常见类型及解法：

已知条件

解法步骤

Rt△ABC

两

边

两直角边（a，b）

由

求∠A，

∠B=90°

－∠A，

斜边，一直角边（如c，a）

一

角

一直角边

和一锐角

锐角、邻边

（如∠A，b）

锐角、对边

（如∠A，a）

斜边、锐角（如c，∠A）

2．用解直角三角形的知识解决实际问题的基本方法是：

　　把实际问题抽象成数学问题（解直角三角形），就是要舍去实际事物的具体内容，把事物及它们的联系转化为图形（点、线、角等）以及图形之间的大小或位置关系．

　　借助生活常识以及课本中一些概念（如俯角、仰角、倾斜角、坡度、坡角等）的意义，也有助于把实际问题抽象为数学问题．

　　当需要求解的三角形不是直角三角形时，应恰当地作高，化斜三角形为直角三角形再求解．

3．锐角三角函数的应用

　　用相似三角形边的比的计算具有一般性，适用于所有形状的三角形，而三角函数的计算是在直角三角形中解决问题，所以在直角三角形中先考虑三角函数，可以使过程简洁。

　　如：

射影定理不能直接用，但是用等角的三角函数值相等进行代换很简单：

　　　　∵

　　　　∴

【典型例题】

类型一、锐角三角函数

1．在Rt△ABC中，∠C＝90°

，若将各边长度都扩大为原来的2倍，则∠A的余切值（）．

A．扩大2倍B．缩小2倍C．扩大4倍D．不变

【答案】D；

【解析】根据

知cot∠A的值与∠A的大小有关，与

的比值有关．

当各边长度都扩大为原来的2倍时，其

的比值不变．故选D.

【总结升华】锐角三角函数正弦、余弦、正切和余切反映了直角三角形中边与边的关系．

举一反三：

【变式1】已知，如图，

中，

，求cosA及tanA．

【答案】易证点B、C、D、E四点共圆，△ADE∽△ABC，

cosA=

tanA=

【变式2】如图所示，已知△ABC是⊙O的内接三角形，AB＝c，AC＝b，BC＝a，请你证明

．

【答案】

证明：

⊙O是△ABC的外接圆，设圆的半径为R，

连结AO并延长交⊙O于点D，连结CD，则∠B＝∠D．

∵AD是⊙O的直径，∴∠ACD＝90°

．即△ACD为直角三角形．

∴

，∴

同理可证：

类型二、特殊角三角函数值的计算

2．已知a＝3，且

，则以a、b、c为边长的三角形面积等于（）．

A．6B．7C．8D．9

【答案】A；

【解析】根据题意知

解得

所以a＝3，b＝4，c＝5，即

，其构成的三角形为直角三角形，且∠C＝90°

所以

【总结升华】利用非负数之和等于0的性质，求出b、c的值，再利用勾股定理的逆定理判断三角形是直角三角形，注意tan45°

的值不要记错．

【变式】计算：

【答案】原式=

=

类型三、解直角三角形

3．如图所示，在等腰Rt△ABC中，∠C＝90°

，AC＝6，D是AC上一点，若

，则AD的长为（）．

A．2B．

C．

D．1

【答案】A；

【解析】如何用好

是解题关解，因此要设法构造直角三角形，作DE⊥AB于点E．

∵△ABC为等腰直角三角形，∴∠A＝45°

，∴AE＝DE．

设DE＝x，则AE＝x，由

知BE＝5x，

∴AB＝6x，由勾股定理知AC2+BC2＝AB2，

∴62+62＝（6x）2，∴

∴AD＝

AE＝

【总结升华】在直角三角形中，若已知两边，宜先用勾股定理求出第三边，再求锐角三角函数值；

若已知一边和角，应先求另一角，再通过锐角三角函数列出含有未知元素和已知元素的等式求解．若所在的元素不在直角三角形中，则应将它转化到直角三角形中去，转化的途径及方法很多，如可作辅助线构造直角三角形，或找已知直角三角形中的边或角替代所要求的元素等．

类型四、锐角三角函数与相关知识的综合

4．如图所示，直角△ABC中，∠C＝90°

，AB＝

，sinB＝

，点P为边BC上一动点，PD∥AB，PD交AC于点D，连接AP，

（1）求AC，BC的长；

（2）设PC的长为x，△ADP的面积为y，当x为何值时，y最大，并求出最大值．

【答案与解析】

（1）在Rt△ABC中，由

得AC＝2，由勾股定理得BC＝4．

（2）∵PD∥AB，∴△ABC∽△DPC，∴

∵PC＝x，则

∴当x＝2时，y有最大值，最大值是1．

【总结升华】

（1）在Rt△ABC中，由AB＝

，易得AC＝2，再由勾股定理求BC．

（2）

，只要把AD用x表示即可求出△ADP的面积y，

由PD∥AB可得

，从而求出

，则

【变式】如图，设P是矩形ABCD的AD边上一动点，

于点E，

于F，

求

的值．

【答案】如图，sin∠1=

sin∠2=

由矩形ABCD知∠1=∠2，

则PE=PAsin∠1，PF=PDsin∠2,sin∠1=

所以PE+PF=PAsin∠1+PDsin∠2=（PA+PD）sin∠1=

类型五、三角函数与实际问题

5．某乡镇中学教学楼对面是一座小山，去年“联通”公司在山顶上建了座通讯铁塔．甲、乙两位同学想测出铁塔的高度，他们用测角器作了如下操作：

甲在教学楼顶A处测得塔尖M的仰角为α，塔座N的仰角为β；

乙在一楼B处只能望到塔尖M，测得仰角为θ（望不到底座），他们知道楼高AB＝20m，通过查表得：

＝0.5723，

0.2191，

＝0.7489，请你根据这几个数据，结合图形推算出铁塔高度MN的值．

【答案与解析】

如图所示，设地平线BD、水平线AE分别交直线MN于D、E，显然AE＝BD，不妨设为m，

则在Rt△AEM中，ME＝mtanα，

在Rt△AEN中，NE＝mtanβ．

∴MN＝m（tanα－tanβ）．

在Rt△BDM中，MD＝mtanθ，

而AB＝DE＝MD－ME＝m（tanθ－tanα），

将AB＝20（m），

＝0.5723，

0.7489代入得MN＝40（m）．

∴可测得铁塔的高度MN＝40m.

【总结升华】构造直角三角形，把实际问题转化为解直角三角形问题.

6．如图所示，帆船A和