小学四年级数学易错题.docx

小学四年级数学易错题.docx

《小学四年级数学易错题.docx》由会员分享，可在线阅读，更多相关《小学四年级数学易错题.docx（8页珍藏版）》请在冰豆网上搜索。

小学四年级数学易错题

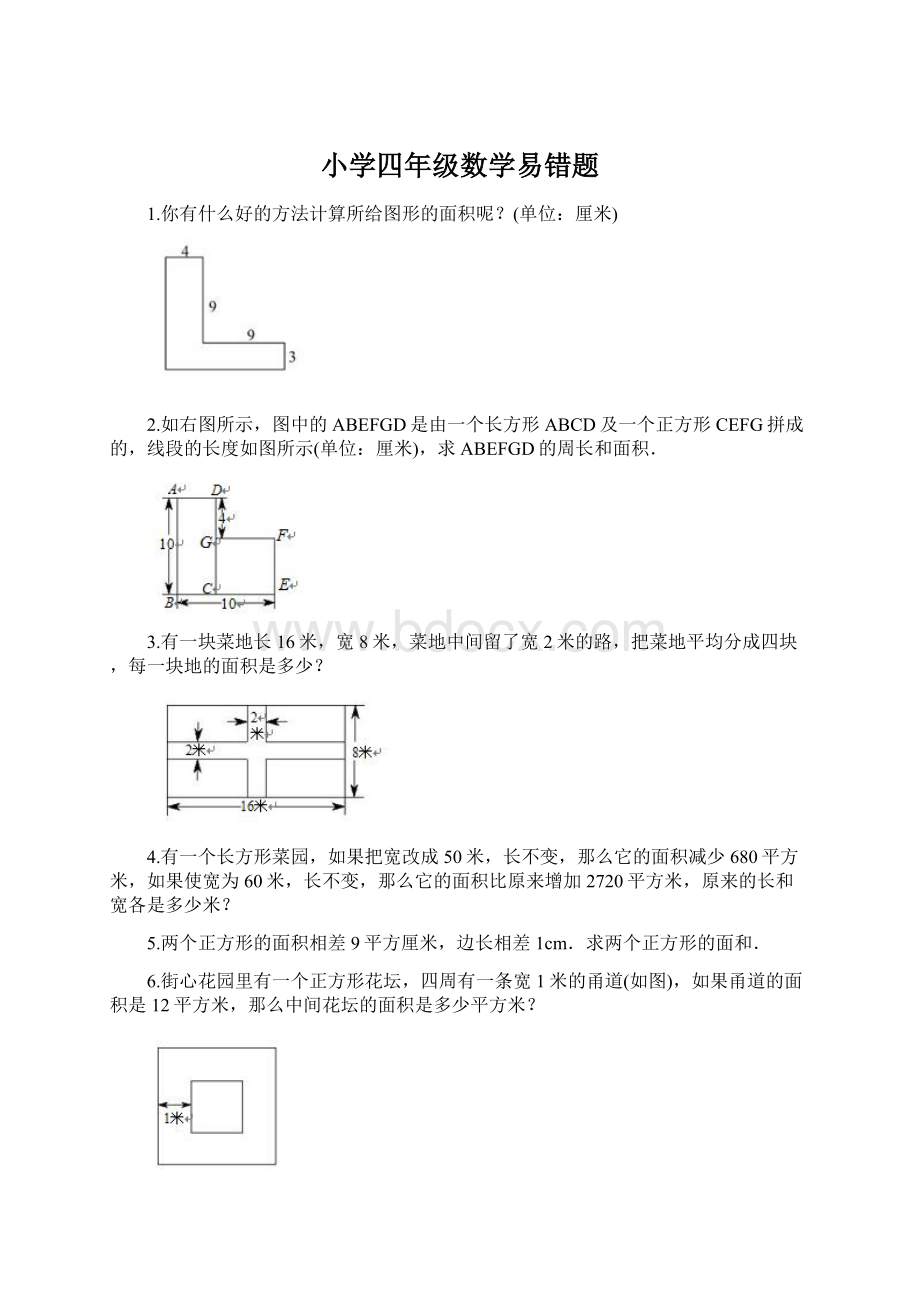
1.你有什么好的方法计算所给图形的面积呢？

（单位：

厘米）

2.如右图所示，图中的ABEFGD是由一个长方形ABCD及一个正方形CEFG拼成的，线段的长度如图所示（单位：

厘米），求ABEFGD的周长和面积．

3.有一块菜地长16米，宽8米，菜地中间留了宽2米的路，把菜地平均分成四块，每一块地的面积是多少？

4.有一个长方形菜园，如果把宽改成50米，长不变，那么它的面积减少680平方米，如果使宽为60米，长不变，那么它的面积比原来增加2720平方米，原来的长和宽各是多少米？

5.两个正方形的面积相差9平方厘米，边长相差1cm．求两个正方形的面和．

6.街心花园里有一个正方形花坛，四周有一条宽1米的甬道（如图），如果甬道的面积是12平方米，那么中间花坛的面积是多少平方米？

7.如图所示，一个长方形广场的正中央有一个长方形的水池．水池长8米、宽3米．水池周围用边长为1米的方砖一圈一圈地向外铺．恰好铺了若干圈，共用了152块方砖，那么共铺了多少圈

8.一块长方形纸片，在长边剪去5cm，宽边剪去2cm后（如图），得到的正方形面积比原长方形面积少31平方厘米．求原长方形纸片的面积．

1.（方法一）采用分割法，可给原图分成两个长方形，（图1或图2）两个长方形的总面积就

是所求的面积．图1的面积是：

4×（9+3）+9×3=75（平方厘米）．图2的面积

是：

（9+4）×3+9×4=75（平方厘米）．

（方法二）采用补图法，如果补上一个边长是9厘米的正方形（图3），就成了一个面积是：

（4+9）×（9+3）=156（平方厘米）的大长方形．因此用这个长方形的面积减去所补正方形的面积，就是要求的图形面积（4+9）×（9+3）-9×9=75（平方厘米）．

2.方法一：

如果求出长方形的宽及正方形的边长，则图形ABEFGD的周长和面积可以求出．而正方形的边长GC=DC-DG=AB-DG=10-4=6（厘米），长方形的宽=BE-CE=10-6=4（厘米），所求图形的周长=10×2+6×2+4+4=40（厘米），面积=S长方形ABCD+S正方形CEFG=10×4+6×6=76（平方厘米）

方法二：

可以将线段GF、DG向外平移，得一个新的图形ABEH，因为DG=HF，GF=DH，所以图形ABEH的周长就是图形ABEFGD的周长．而AB=BE=10（厘米），所以图形ABEH是边长为10厘米的正方形．所求图形的周长=正方形ABEH的周长=10×4=40（厘米），面积=S正方形ABEH-S长方形DGFH=10×10-6×4=76（平方厘米）

3.方法一：

可以直接求出每小块菜地的长和宽，从而求出每小块菜地的面积；每一块地的面积是：

（[16-2）÷2]×（[8-2）÷2]=7×3=21（平方米）

方法二：

也可以求出这块地的总面积，再减去道路的面积，然后把剩余的面积四等分求出每小块菜地的面积；每一块地的面积是：

[16×8-（2×16+8×2-2×2）]÷4=（128-44）÷4=21（平方米）

4.根据题意，可以用下图表示增减变化的情况，从图中可以看出，原来长方形的长为（2720+680）÷（60-50）=340（米），宽为680÷340+50=52（米）．

6.把甬道的部分分成四个同样大的长方形，每个长方形的面积是12¸4=3（平方米）．因为水泥路宽1米，所以小长方形长是3¸1=3（米），而正方形花坛的边长是小长方形长与宽的差，即2米，中间花坛的面积是：

（3-1）×（3-1）=4（平方米）．

7.水池的面积是8×3=24，铺完之后水池加上地砖的面积是176=16×11．由于每铺一圈都会是边长增加2，所以铺了8÷2=4（圈）．

8.通过对图形进行分割，可以发现C的长与宽分别是5cm和2cm，则它的面积是5×2=10（C㎡），那么A+B的面积是31-10=21（C㎡），如给B移到A的旁边，则知正方形的

边长：

3（cm），正方形的面积是3×3=9（C㎡），原长方形的面积是31+9=40（C㎡）

四年级练习题之二

1.有一个长方形，如果它的宽减少2厘米，或它的长减少3厘米，它的面积都奖减少24平方厘米。

求这个长方形原来的面积

2.一块正方形的钢板，先截去5分米的长方形，再截去赛为8分米的长方形，这时剩下的图形比原来正方形的面积减少181平方分米，原来正方形的边长是多少分米？

4.一个长方形，如果宽不变，长增加8米，面积增加72平方米；如果长不变，宽减少4米，面积就减少48平方米，这个长方形原来的面积是多少平方米？

5.一个长方形的周长是50厘米，长比宽多5厘米，那么此长方形的面积是____平方厘米。

6..最上面图中长方形长30厘米，宽15厘米，阴影部分面积是____平方厘米。

9.一个正方形，如果边长增加1厘米，那么面积增加17平方厘米。

这个正方形原来面积是____平方厘米。

11.大正方形的面积比小正方形的面积多24平方米，小正方形的面积是多少？

12.一个长方形，如果宽增加2厘米，或长增加3厘米，它们的面积都增加120平方厘米，原来长方形的面积是多少？

13.用长44厘米的铁丝围成各种长方形（长和宽都是整厘米，长和宽不相等），围成的长方形最大面积是多少平方厘米？

14.一个长方形的周长是22厘米，如果它的长和宽为整厘米数，这个长方形的面积有多少种可能？

15.将一个边长为4分米的正方形改成一个长方形，围成的最大的长方形的面积是多少平方分米？

16.这是由5个相同的小长方形拼成的一个大长方形，大长方形的周长是66厘米？

求大长方形有的面积。

17.10个相同的小长方形拼成一个大长方形，已知小方形的宽是15厘米，求大长方形的面积是多少平方厘米?

18.一个边长为40厘米的正方形，依次连接四边中点得到第二个正方形，这样继续下去可得到第三个、第四个正方形，求第四个正方形的面积。

19.长方形ABCD周长是18米，在它的每条边上各玏一个以该边为边长的正方形，已知这四具正方表的面积的放是78平方米，求长方形ABCD的面积。

20.一个长方形周长是24厘米，在它的每条边上各玏一个以该边为边长的正方形，已知新玏的四个正形的面积之和是208平方厘米，问原来长方形（阴影）的面积是多少平方厘米？

21.一个长方形，周长是36厘米，长比宽长4厘米，求这个长方形抽面积

22.一个长方形，周长是36厘米，长是宽的2倍，这个长方形的面积是多少平方厘米？

23、有一块长方形果园，它的长是80米，宽比长短35米，整个果园占地面积是多少？

如果要在果园的四周围上篱笆，篱笆的长是多少？

【1】用20米长的护栏在一片空地上围成一个种花草的长方形的苗圃，如果每边的长度都是整数，那么有几种围法？

怎样才能使苗圃的面积最大？

最大面积与最小面积各是多少？

【2】四个相同的小长方形拼成一个大长方形，已知小长方形的宽是15厘米，求大长方形的面积是多少平方厘米？

【3】有一个正方形水池，在它的周围修一个宽2米的路，这条路的面积是120平方米，求水池的面积。

【4】一个长方形的周长是70厘米，长比宽长5厘米，需同时减少长和宽，使减少以后的长方形的面积是原来长方形面积的一半。

如果长减少5厘米，宽应当减少多少厘米？

【5】一个长方形木板，如果长减少5分米，宽减少3分米，那么它的面积就减少71平方分米，这时剩下的部分恰好是一个正方形，求原来长方形的面积。

【6】一个正方形的一条边减少6厘米，另一条边减少10厘米后变成一个长方形，这个长方形的面积比正方形的面积少260平方厘米，求原来正方形的边长。

【7】右图是一个边长为8厘米的正方形，我们称它为第一个正方形，依次连接四条边的中点得到第二个正方形，继续这样，得到第三个、第四个，则第一个正方形至第四个正方形的面积之和是多少平方厘米？

【8】一个长方形被分成四个小长方形，求图中？

部分的面积。

（单位：

平方厘米）

【答案】

【1】用20米长的护栏在一片空地上围成一个种花草的长方形的苗圃，如果每边的长度都是整数，那么有几种围法？

怎样才能使苗圃的面积最大？

最大面积与最小面积各是多少？

长 9 8 7 6 5

宽 1 2 3 4 5

面积 9 16 21 24 25

【2】四个相同的小长方形拼成一个大长方形，已知小长方形的宽是15厘米，求大长方形的面积是多少平方厘米？

   4个宽=3个长，4×15÷3=20厘米，20×3=60厘米，15+20+15=50厘米

   50×60=3000平方厘米

【3】有一个正方形水池，在它的周围修一个宽2米的路，这条路的面积是120平方米，求水池的面积。

2×2×4=16平方米，（120-16）÷4=26平方米，26÷2=13米，13×13=169平方米

【4】一个长方形的周长是70厘米，长比宽长5厘米，需同时减少长和宽，使减少以后的长方形的面积是原来长方形面积的一半。

如果长减少5厘米，宽应当减少多少厘米？

5厘米，提示：

原长方形长为20厘米，宽为15厘米

【5】一个长方形木板，如果长减少5分米，宽减少3分米，那么它的面积就减少71平方分米，这时剩下的部分恰好是一个正方形，求原来长方形的面积。

71-5×3=56平方分米，56÷（3+5）=7分米，7×7=49平方分米

【6】一个正方形的一条边减少6厘米，另一条边减少10厘米后变成一个长方形，这个长方形的面积比正方形的面积少260平方厘米，求原来正方形的边长。

（260+6×10）÷（6+10）=20厘米

【7】右图是一个边长为8厘米的正方形，我们称它为第一个正方形，依次连接四条边的中点得到第二个正方形，继续这样，得到第三个、第四个，则第一个正方形至第四个正方形的面积之和是多少平方厘米？

8×8÷2÷2÷2=8平方厘米，64+32+16+8=120平方厘米

【8】一个长方形被分成四个小长方形，求图中？

部分的面积。

（单位：

平方厘米）

  60平方厘米

【经典例题1】用15米长的木兰沿着围墙围一个种花草的长方形或者正方形的苗圃，其中一面利用围墙，如果每边的长度都是整数，那么有几种围法，怎样围才能使围成的面积最大？

【经典例题2】一个正方形的花坛，四周有1米宽的水泥路。

如果水泥路的总面积是12平方米，中间花坛的面积是多少平方米？

【经典例题3】如图，将相同的小长方形拼成一个大长方形，已知小长方形的宽是12厘米，求大长方形的面积。

【经典例题4】一张长方形纸片，在长边上剪下5厘米，宽边上剪下2厘米，余下的部分正好是一个正方形，已知正方形的面积比原来长方形面积少66平方厘米，求正方形面积。

【经典例题5】一块正方形的玻璃，一边截去12厘米，另一边截去8厘米，剩下的长方形面积比原来的正方形减少1764平方厘米，原正方形玻璃的周长是多少厘米？

【经典例题6】一个边长为20厘米的正方形，依次连接四边中点得到第二个正方形，这样继续下去可得到第三个，第四个，第五个正方形，求第五个正方形的面积。

【经典例题7】如图，是一个楼梯的截面图，高280厘米，每阶台阶的宽和高都是20厘米，这楼梯的截面积是多少平方厘米？

【经典例题8】如图，一个长方形，用垂直长和宽的两条线段分成四块，其中三块面积分别为10平方米，14平方米，42平方米，第四块面积是多少平方米？

【答案】

【经典例题1】用15米长的木兰沿着围墙围一个种花草的长方形或者正方形的苗圃，其中一面利用围墙，如果每边的长度都是整数，那么有几种围法，怎样围才能使围成的面积最大？

一条边 7 6 5 4 3 2 1

另一条边 1 3 5 7 9 11 13

【经典例题2】一个正方形的花坛，四周有1米宽的水泥路。

如果水泥路的总面积是12平方米，中间花坛的面积是多少平方米？

     已知12平方米是4个完全相同的长方形组成的