北京市房山区届九年级数学下学期期中试题.docx

北京市房山区届九年级数学下学期期中试题.docx

《北京市房山区届九年级数学下学期期中试题.docx》由会员分享，可在线阅读，更多相关《北京市房山区届九年级数学下学期期中试题.docx（19页珍藏版）》请在冰豆网上搜索。

北京市房山区届九年级数学下学期期中试题

北京市房山区2018届九年级数学下学期期中试题

一、选择题（本题共16分，每小题2分）

下面各题均有四个选项，其中只有一个是符合题意的．

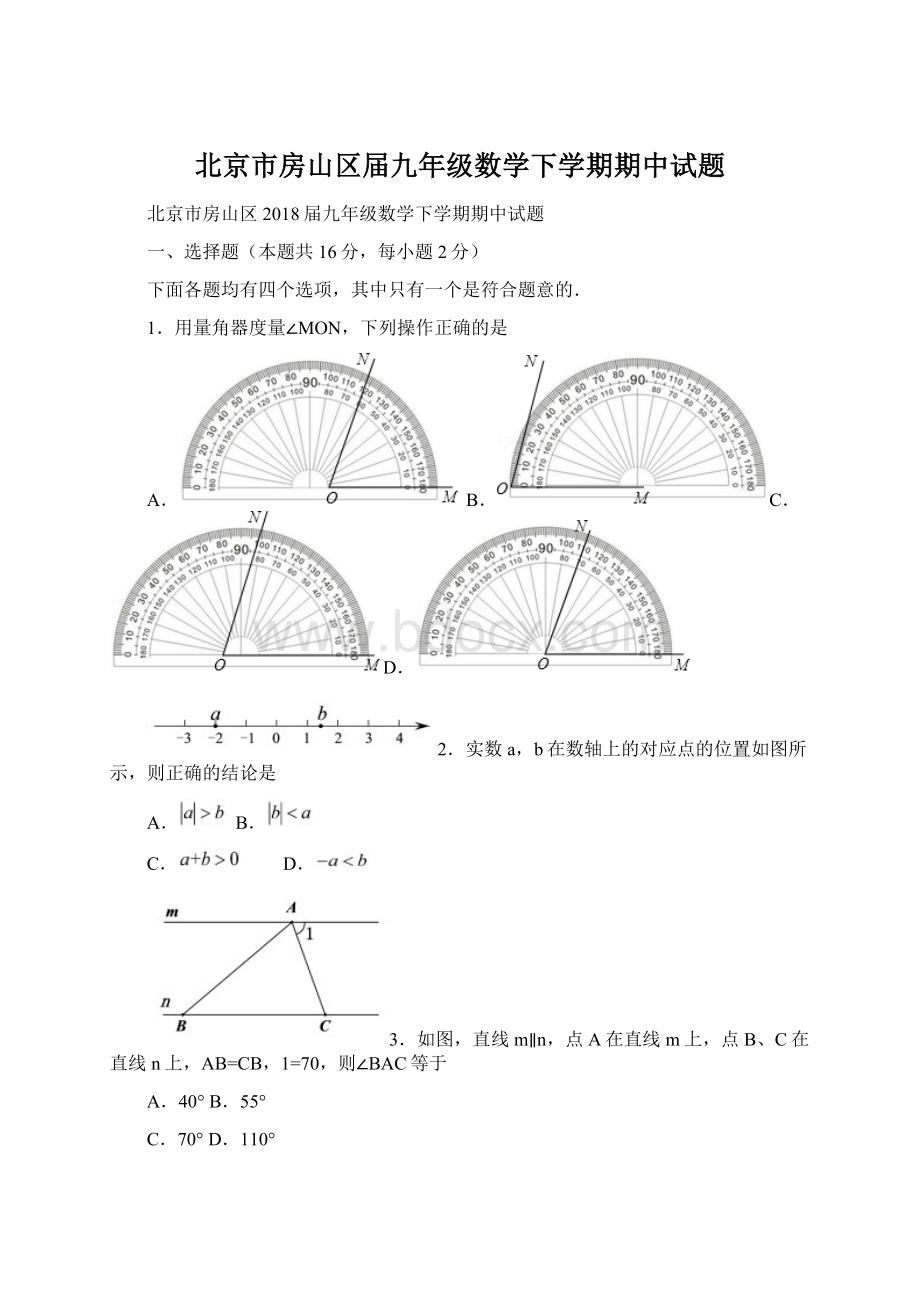
1．用量角器度量∠MON，下列操作正确的是

A．B．C．D．

2．实数a，b在数轴上的对应点的位置如图所示，则正确的结论是

A．B．　

C．　　D．

3．如图，直线m∥n，点A在直线m上，点B、C在直线n上，AB=CB，1=70，则∠BAC等于

A．40°B．55°

C．70°D．110°

4．下列图形中，既是轴对称图形又是中心对称图形的是

A．B．C．D．

5.如图，在⊙O中，AC为⊙O直径，B为圆上一点，若∠OBC=26°，则∠AOB的度数为

A．26°B．52°C．54°D．56°

6.某班体育委员对本班所有学生一周锻炼时间（单位：

小时）进行了统计，绘制了统计图，如图所示，根据统计图提供的信息，下列推断正确的是

A.该班学生一周锻炼时间的中位数是11　

B.该班学生共有44人

C.该班学生一周锻炼时间的众数是10　

D.该班学生一周锻炼12小时的有9人

7.如果，那么代数式的值是

A.B.C.D.1

8.小宇在周日上午8：

00从家出发，乘车1小时到达某活动中心参加实践活动．11：

00时他在活动中心接到爸爸的电话，因急事要求他在12：

00前回到家，他即刻按照来活动中心时的路线，以5千米/时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家x小时后，到达离家y千米的地方，图中折线OABCD表示y与x之间的函数关系．下列叙述错误的是

A．活动中心与小宇家相距22千米

B.小宇在活动中心活动时间为2小时

C.他从活动中心返家时，步行用了0.4小时

D.小宇不能在12：

00前回到家

二、填空题（本题共16分，每小题2分）

9．如果二次根式有意义，那么x的取值范围是__________．

10.如图，正方形ABCD，根据图形，写出一个正确的等式：

__________．

11.中国古代数学著作《算法统宗》中有这样一段记载：

“三百七十八里关，初日健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是：

有人要去某关口，路程为378里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地．若求此人第六天走的路程为多少里．设此人第六天走的路程为x里,依题意，可列方程为__________．

12.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：

甲

乙

丙

丁

平均数

9.14

9.15

9.14

9.15

方差

6.6

6.8

6.7

6.6

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择_________．

13.一个正方形和两个等边三角形的位置如图所示，

则∠1+∠2+∠3的度数为_________．

14.下表记录了一名球员在罚球线上投篮的结果.

投篮次数n

100

150

300

500

800

1000

投中次数m

60

96

174

302

484

602

投中频率

0.600

0.640

0.580

0.604

0.605

0.602

估计这名球员在罚球线上投篮一次，投中的概率为__________．

15.如图，甲、乙为两座建筑物，它们之间的水平距离BC为30m，

在A点测得D点的仰角∠EAD为45°，在B点测得D点的仰角

∠CBD为60°，则甲建筑物的高度为__________m，乙建筑物

的高度为__________m．

16.如图，在平面直角坐标系xOy中，点A（－3，0），

B（－1，2）.以原点O为旋转中心，将△AOB顺时针旋转90°，再沿x轴向右平移两个单位，得到△A’O’B’，其中点A’与点A对应，点B’与点B对应.则点A’的坐标为__________，点B’的坐标为__________．

三、解答题（本题共68分，第17－23题，每小题5分，第24题6分，第25题6分，第26题6分，第27题7分，第28题8分）

17.计算：

18.解不等式：

，并把它的解集在数轴上表示出来.

19．如图，在△ABC中，AB=AC，点，在边上，．

求证：

．

20．关于x的一元二次方程有两个不相等的实数根.

（1）求m的取值范围；

（2）写出一个满足条件的m的值，并求此时方程的根.

21.如图，在中，，点分别是上的中点，连接并延长至点，使，连接.

（1）证明：

；

（2）若，AC=2，连接BF，求BF的长

22．如图，AB、BF分别是⊙O的直径和弦，弦CD与AB、BF分别相交于点E、G，过点F的切线HF与DC的延长线相交于点H，且HF＝HG.

（1）求证：

AB⊥CD；

（2）若sin∠HGF＝，BF＝3，求⊙O的半径长.

23.如图，直线与反比例函数的图象交于点，与轴交于点，与轴交于点．

（1）求的值和反比例函数的表达式；

（2）在y轴上有一动点P（0，n），过点P作平行于轴的直线,交反比例函数的图象于点，交直线于点，连接．若，求的值．

24.某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每个营业员在某月的销售额（单位：

万元），数据如下，请补充完整．

收集数据17181612241527251819

22171619312916141525

15312317151527271619

整理、描述数据

销售额/万元

12

14

15

16

17

18

19

22

23

24

25

27

29

31

人数

1

1

4

3

2

1

1

1

2

3

1

2

分析数据样本数据的平均数、众数、中位数如下表所示：

平均数

众数

中位数

20

18

得出结论⑴如果想让一半左右的营业员都能达到销售目标，你认为月销售额应定为

万元．

⑵如果想确定一个较高的销售目标，这个目标可以定为每月万元，理由为．

25.如图，Rt△ABC，∠C=90°，CA=CB=4cm，点P为AB边上的一个动点，点E是CA边的中点,连接PE，设A，P两点间的距离为xcm，P，E两点间的距离为ycm.

小安根据学习函数的经验，对函数随自变量的变化而变化的规律进行了探究．

下面是小安的探究过程，请补充完整：

（1）通过取点、画图、测量，得到了与的几组值，如下表：

x/cm

0

1

2

3

4

5

6

7

8

y/cm

2.8

2.2

2.0

2.2

2.8

3.6

5.4

6.3

（说明：

补全表格时相关数值保留一位小数）

（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

（3）结合画出的函数图象，解决问题：

①写出该函数的一条性质：

；

②当时，的长度约为cm.

26.抛物线分别交x轴于点A（－1,0），C（3，0），交y轴于点B，抛物线的对称轴与x轴相交于点D.点P为线段OB上的点，点E为线段AB上的点，且PE⊥AB.

（1）求抛物线的表达式；

（2）计算的值；

（3）请直接写出的最小值为.

27.如图，已知Rt△ABC中，∠C=90°，∠BAC=30°，点D为边BC上的点，连接AD，∠BAD=α，点D关于AB的对称点为E，点E关于AC的对称点为G，线段EG交AB于点F，连接AE，DE，DG，AG.

（1）依题意补全图形；

（2）求∠AGE的度数（用含α的式子表示）；

（3）用等式表示线段EG与EF，AF之间的数量关系，并说明理由.

28.在平面直角坐标系xOy中，当图形W上的点P的横坐标和纵坐标相等时，则称点P为图形W的“梦之点”.

（1）已知⊙O的半径为1.

①在点E（1,1），F（,－）,M（－2，－2）中，⊙O的“梦之点”为；

②若点P位于⊙O内部，且为双曲线（k≠0）的“梦之点”，求k的取值范围.

（2）已知点C的坐标为（1，t），⊙C的半径为，若在⊙C上存在“梦之点”P，直接写出t的取值范围.

（3）若二次函数的图象上存在两个“梦之点”，,且，求二次函数图象的顶点坐标.

房山区2017—2018学年度第二学期期中检测试卷

九年级数学参考答案

一、选择题（本题共16分，每小题2分）

题号

1

2

3

4

5

6

7

8

答案

D

A

C

B

B

A

A

D

二、填空题（本题共16分，每小题2分）

9.x≥-4;10.;

11.;12.丁；

13.150°；14.（0.600附近即可）;

15.，；16.（2，3），（4，1）.

三、解答题（本题共68分，第17－23题，每小题5分，第24题6分，第25题6分，第26题6分，第27题7分，第28题8分）

17.解：

原式=………………………………………………………4分

=…………………………………………………………………………5分

18.解：

………………………………………………………………………1分

…………………………………………………………………3分

……………………………………………………………………………4分

解集在数轴上表示如下：

……………………………………………………………………………5分

19.解：

法1：

∵AB=AC

∴∠B=∠C………………………………………………………………………1分

∵AD=CE

∴∠ADE=∠AED…………………………………………………………………2分

∴△ABE≌△ACD………………………………………………………………3分

∴BE=CD…………………………………………………………………………4分

∴BD=CE……………………………………………………………………………5分

法2：

如图，作AF⊥BC于F

∵AB=AC

∴BF=CF…………………………………2分

∵AD=AE

∴DF=EF………………………………………………………………………………4分

∴BF－DF=CF－EF

即BD=CE………………………………………………………………………………5分

20.解:

（1）由题意得，

解得，……………………………………………………………………2分

（2）当时………………………………………………………………………3分

方程为

解得，…………………………………………………………5分

【注：

答案不唯一】

21.解：

（1）∵D，E分别是BC，AB上的中点

∴DE为△ABC的中位线

∴DE∥AC，AC=2DE……………………………………………………………1分

又∵DF=2DE

∴EF=AC

∴四边形ACEF为平行四边形

∴AF=CE…………………………………………………………………………2分

（2）∵∠ABC=90°，∠B=30°，AC=2

∴BC=2,DE=1,∠EDB=90