一线三等角.docx

一线三等角.docx

《一线三等角.docx》由会员分享，可在线阅读，更多相关《一线三等角.docx（6页珍藏版）》请在冰豆网上搜索。

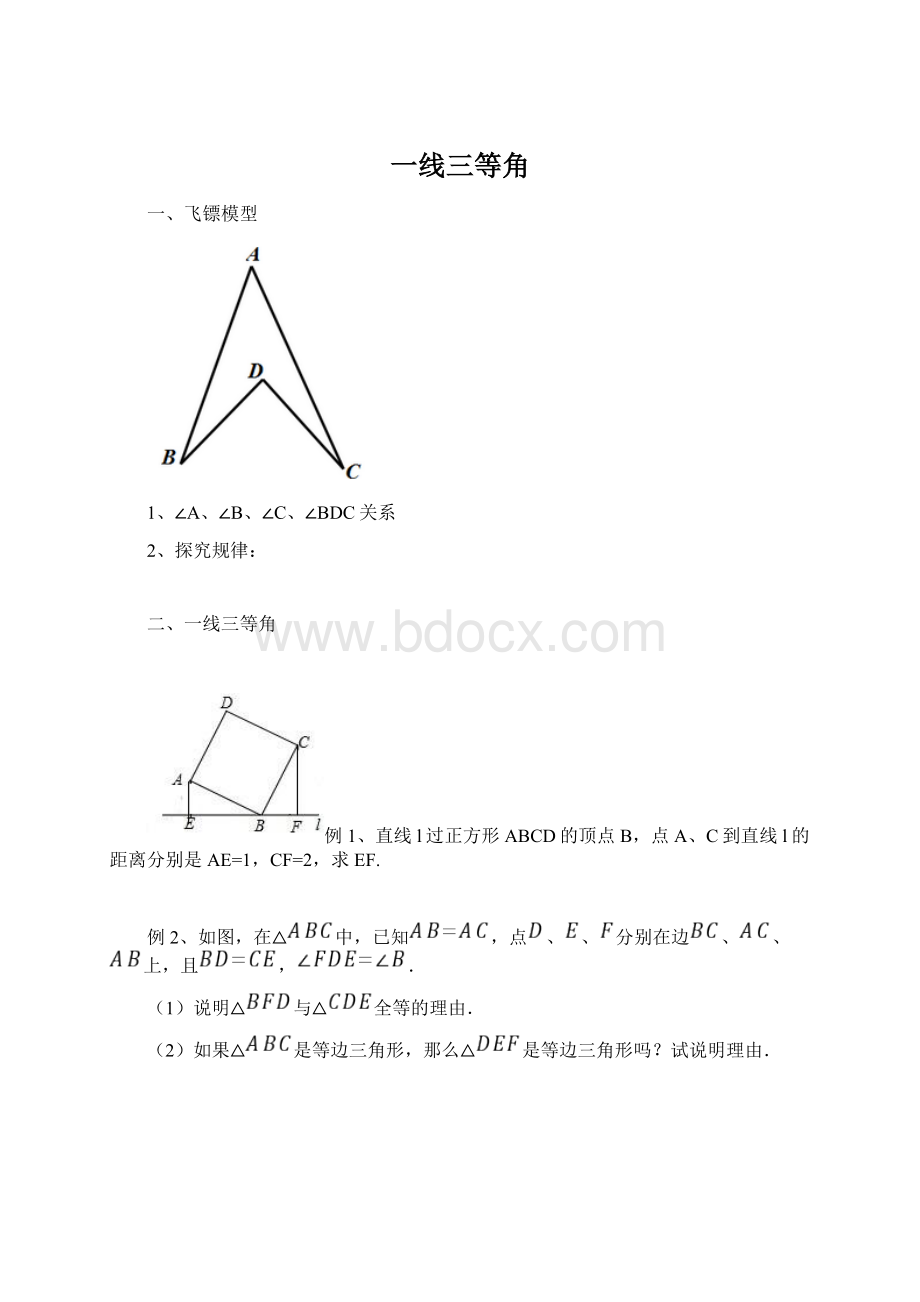
一线三等角

一、飞镖模型

1、∠A、∠B、∠C、∠BDC关系

2、探究规律：

二、一线三等角

例1、直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是AE=1，CF=2，求EF.

例2、如图，在△中，已知，点、、分别在边、、上，且，．

（1）说明△与△全等的理由．

（2）如果△是等边三角形，那么△是等边三角形吗？

试说明理由．

例3、如图，已知点C是线段AB上一点，∠DCE＝∠A＝∠B，CD＝CE．

（1）说明△ACD与△BCE全等的理由；

（2）判断线段AB、AD、BE之间的数量关系，并说明理由．

拓展1.如图①，在△ABC中，∠ACB=90°，AC=BC，过点C在△ABC外作直线MN，AM⊥MN于点M，BN⊥MN于点N.

（1）试说明：

MN=AN+BN.

（2）如图②，若过点C作直线MN与线段AB相交，AM⊥MN于点M，BN⊥MN于点N（AM＞BN），

（1）中的结论是否仍然成立？

说明理由.

拓展2.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动（点D不与点B、C重合）,连接AD,作∠ADE=40°,DE交线段AC于点E.

（1）当∠BDA=115°时,∠EDC=；∠AED=

（2）线段DC的长度为何值时,△ABD≌△DCE,请说明理由;

（3）在点D的运动过程中,△ADE的形状可以是等腰三角形吗?

若可以,求∠BDA的度数;若不可以,请说明理由.

拓展3.

（1）某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:

在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD垂直直线l,垂直直线l,垂足分别为点D、E.证明:

DE=BD+CE.

（2）组员小刘想,如果三个角不是直角,那结论是否会成立呢?

如图

（2）,将

（1）中的条件改为:

在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?

如成立,请你给出证明;若不成立,请说明理由.

（3）数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:

如图（3）,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:

I是EG的中点.

拓展4.

（1）如图1，已知：

在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD垂直直线m，CE垂直直线m，垂足分别为点D、E。

证明：

DE=BD+CE。

（2）如图2，将

（1）中的条件改为：

在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角。

请问结论DE=BD+CE是否成立？

如成立，请你给出证明；若不成立，请说明理由。

（3）拓展与应用：

如图3，D、E是D、A、E三点所在直线上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状。

拓展5.如图1，有一组平行线l1∥l2∥l3∥l4，正方形ABCD的四个顶点分别在l1,l2,l3,l4上，EG过点D且垂直l1于点E，分别交l2，l4于点F，G，EF=DG=1，DF=2。

（1）AE=_____ ，正方形ABCD的边长=_____ 。

（2）如图2，将∠AEG绕点A顺时针旋转得到∠AE,D,，旋转角为（0°＜α＜90°），点D,在直线l3上，以AD，为边在E,D,左侧作菱形AB，C，D，，使B，，C，分别在直线l2，l4上。

①写出∠B，AD，与α的数量关系并给出证明。

②若α=30°，求菱形AB，C，D，的边长。

三角形辅助线常用方法

一、出现角平分线时，常在角的两边截取相等的线段，构造全等三角形

例1、如图,在△ABC中∠1＝∠2,∠3＝∠4,∠A＝60°,求证:

CD+BE=BC.

例2、已知：

如图，在△ABC中，∠C＝2∠B，AD平分∠BAC，求证：

AB－AC＝CD.

练习1、如图,AB∥CD,BE、CE分别是∠ABC和∠BCD的平分线,点E在AD上.

求证:

BC=AB+CD.

练习2、如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC,∠ACB，则AC的长与AE+CD的关系是（    ）

A. AC=AE+CD

B. AC＞AE+CD

C.AC＜AE+CD

D. 无法确定

二、出现线段的中点或三角形的中线时，可利用中线倍长法构造全等三角形

例3、如图，△ABC中，AD是BC边上的中线，求证AD＜（AB+BC）

例4、如图，AD是△ABC的中线，BE交AC于E交AD于F，且AE=EF求证：

AC=BF

练习1、已知△ABC中AB=4，BC=6，BD是AC边上中线，求BD的取值范围。

练习2、已知:

在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,

求证:

AF=EF.