雷达信号处理的MATLAB仿真.docx

雷达信号处理的MATLAB仿真.docx

《雷达信号处理的MATLAB仿真.docx》由会员分享，可在线阅读，更多相关《雷达信号处理的MATLAB仿真.docx（14页珍藏版）》请在冰豆网上搜索。

雷达信号处理的MATLAB仿真

11目录

1设计的基本骤

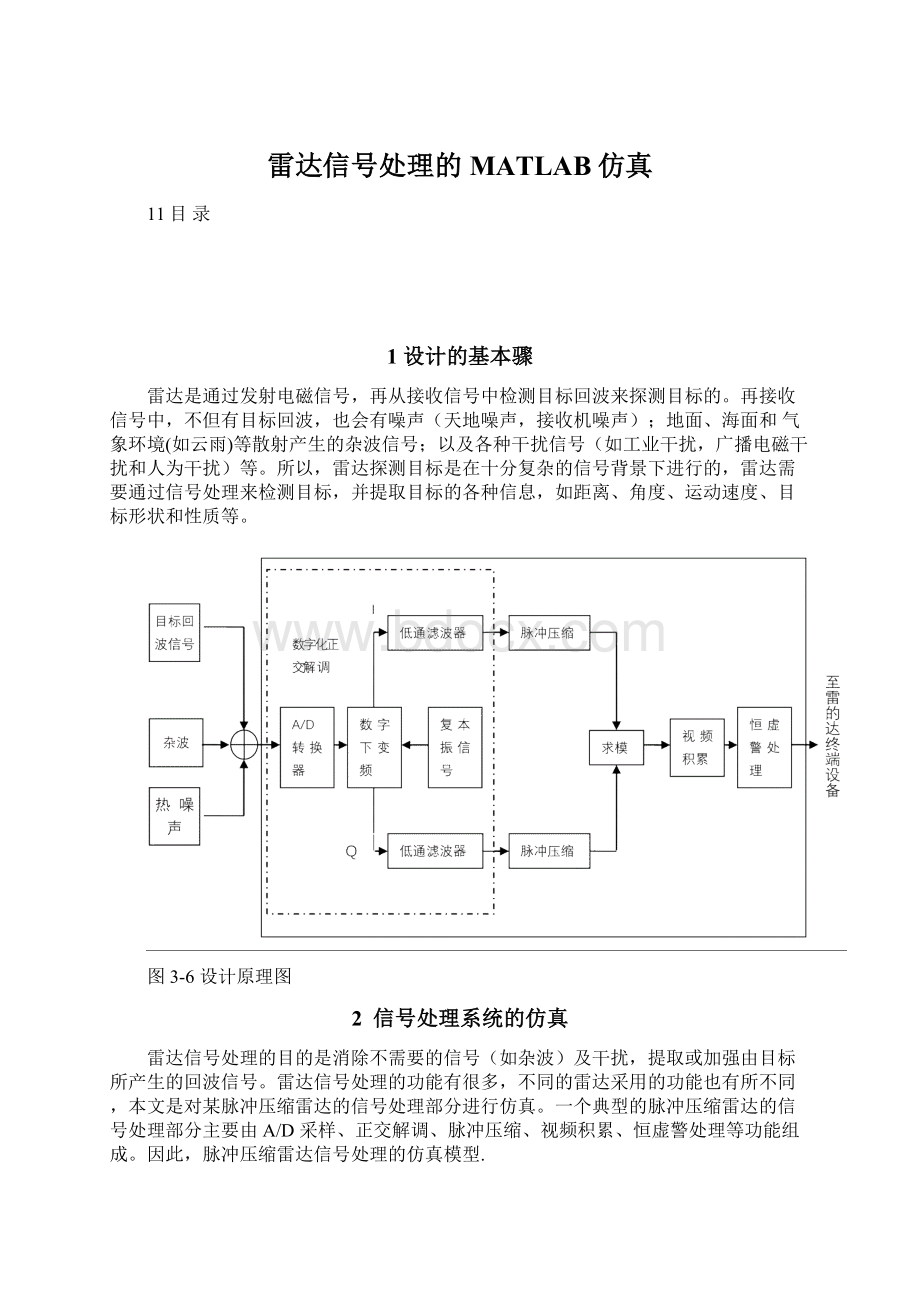
雷达是通过发射电磁信号，再从接收信号中检测目标回波来探测目标的。

再接收信号中，不但有目标回波，也会有噪声（天地噪声，接收机噪声）；地面、海面和气象环境（如云雨）等散射产生的杂波信号；以及各种干扰信号（如工业干扰，广播电磁干扰和人为干扰）等。

所以，雷达探测目标是在十分复杂的信号背景下进行的，雷达需要通过信号处理来检测目标，并提取目标的各种信息，如距离、角度、运动速度、目标形状和性质等。

图3-6设计原理图

2信号处理系统的仿真

雷达信号处理的目的是消除不需要的信号（如杂波）及干扰，提取或加强由目标所产生的回波信号。

雷达信号处理的功能有很多，不同的雷达采用的功能也有所不同，本文是对某脉冲压缩雷达的信号处理部分进行仿真。

一个典型的脉冲压缩雷达的信号处理部分主要由A/D采样、正交解调、脉冲压缩、视频积累、恒虚警处理等功能组成。

因此，脉冲压缩雷达信号处理的仿真模型.

2.1正交解调模块

雷达中频信号在进行脉冲压缩之前，需要先转换成零中频的I、Q两路正交信号。

中频信号可表示为:

（3.2）

式（3.2）中，f0为载波频率。

令:

（3.3）

则

（3.4）

在仿真中，所有信号都是用离散时间序列表示的，设采样周期为T,则中频信号为

fIF（rT），同样，复本振信号采样后的信号为

flocal=exp（−jω0rT）（3.5）

则数字化后的中频信号和复本振信号相乘解调后，通过低通滤波器后得到的基带信号fBB（r）为:

（3.6）

式（3.6）中，h（n）是积累长度为N的低通滤波器的脉冲响应。

根据实际的应用，仅仅采用以奈奎斯特采样率进行采样的话，得不到较好混频信号和滤波结果，采样频率fs一般需要中心频率的4倍以上才能获得较好的信号的实部和虚部。

当采样频率为fs=4f0时，ω0T=

/2，则基带信号可以简化为

（3.7）

使用Matlab仿真正交解调的步骤：

（1）产生理想线性调频信号y。

（2）产生I、Q两路本振信号。

设f0为本振信号的中心频率，fs为采样频率，n为线性调频信号时间序列的长度，则I路本振信号为cos（n2

f0/fs）,同样，Q路本振信号sin（n2

f0/fs）。

当fs=4f0时，I、Q两路本信号分别为cos（

n/2）和sin（nπ/2）。

（3）线性调频信号y和复本振信号相乘,得到I、Q两路信号。

（4）I、Q两路信号通过低通滤波器，滤除高频分量，以获得最终的检波结果。

Matlab提供了方便的滤波函数filter（b,a,x）。

其中x为输入信号，b,a为滤波器传递函数的分子和分母的系数向量。

2.2脉冲压缩模块

在进行脉冲压缩处理之前，首先要获得相应的雷达发射信号的匹配滤波器。

在实际工程中，对脉冲压缩的处理往往是在频域实现的，因为这样可以利用FFT算法提高计算速度，然后将雷达回波与匹配滤波器的频域响应（脉冲压缩系数）相乘，再经过IFFT变换，从而得到脉冲压缩处理的结果，而不用进行卷积处理，大大降低了运算量。

因此，在进行脉冲压缩处理仿真的时候，首先应当获取脉冲压缩处理的匹配滤波器或脉冲压缩系数。

求线性调频信号的脉冲压缩系数比较简单，只需要将理想线性调频信号取共轭和翻转即可。

使用Matlab仿真线性调频信号脉冲压缩的步骤：

（1）产生理想线性调频信号y；

（2）对信号正交解调，得到解调后的信号fbb=fbb_i+j*fbb_q；

（3）产生理想线性调频脉冲压缩系数。

这一步要首先求出正交解调后的信号fbb的匹配滤波器，然后利用离散傅里叶变换求出脉冲压缩系数；

（4）产生理想回波信号（signal），对信号进行正交解调。

理想回波信号是一个脉冲重复周期内雷达收到的回波信号，并假设目标为静止点目标；

（5）脉冲压缩处理。

首先对回波信号做离散傅里叶变换，得到signal_fft，然后将signal_fft与匹配滤波器的频域响应（脉冲压缩系数）相乘，再经过离散傅里叶反变换，从而得到脉冲压缩结果。

设雷达发射信号为线性调频信号，具体参数如下：

脉宽10μs、中心频率10MHz、调频带宽2MHz。

对雷达回波信号的采样频率为40MHz，中频进行正交下变频。

2.3回波积累模块

现在的雷达都是在多脉冲观测的基础上进行检测的，多个脉冲积累后可以有效地提高信噪比，从而改善雷达的检测能力。

积累处理可以在包络检波前完成，称为检波前积累或者中频积累。

信号在中频积累时要求信号间有严格的相位关系，也就是说信号是相参的，所以也称为相参积累。

此外，积累过程可以在包络检波后完成，称为检波后积累或者视频积累。

由于信号在包络检波后失去了相位信息而只保留了幅度信息，所以检波后积累处理就不需要信号间有严格的相位关系，因此这种积累又称为非相参积累。

实现非相参积累的方法有很多，例如抽头延迟线积累（FIR积累）器和反馈积累器。

下面介绍抽头延迟线积累（FIR积累）模型。

（1）积累脉冲数积累脉冲数N应该等于天线波束扫过一个点目标时的目标回波个数，即：

束扫过一个点目标时的目标回波个数，即：

（3.8）

式（3.8）中：

BWa为天线方位波束宽度；Δθ为天线在一个脉冲重复周期扫过的角度；Tc为天线扫描一周所需的时间；PRI为脉冲重复周期。

（2）回波幅度调制雷达接收机内部的噪声一般都认为是高斯白噪声，且是平稳随机过程，而回波脉冲的幅度调制还受天线双程场强波瓣图调制。

如果天线场强波瓣图（单程）是sinx/x的形式，则天线主瓣内的脉冲将以如下的权函数加

（3.9）

Δθ为天线在一个脉冲重复周期扫过的角度

2.4恒虚警处理（CFAR）模块

恒虚警处理有多种方法，从大的分类来看，有所谓的均值类CFAR、有序统计量类CFAR和杂波图CFAR等等。

均值类CFAR包括多种实现方式，如单元平均方式、两侧单元平均选大方式、两侧单元平均选小方式等等，其基本理论是相同的。

使用Matlab仿真恒虚警处理的步骤：

（1）产生叠加了瑞利杂波、热噪声的点目标回波。

这一步首先按照上述的方法分别产生高斯热噪声和瑞利杂波，然后与点目标回波进行叠加，叠加时需要对瑞利杂波和热噪声的幅度加权。

（2）对叠加了瑞利杂波、热噪声的点目标回波进行恒虚警处理。

这一步首先要确定参考单元数。

如果参考单元数为16，那么第1点恒虚警处理时噪声均值由其后面的16点噪声决定，第2点到第16点的恒虚警的噪声均值由其前面和后面的16点噪声共同决定，而正常数据点的恒虚警处理的噪声均值由其前后各16点的噪声决定，最后16点的恒虚警处理与前16点相同。

最后输出的信号为每个检测单元与杂波均值估计值的比值。

程序

closeall;

clearall;

clc;

%%%%%%%产生雷达发射信号%%%%%%%%%%%%%%%%

code=[1,1,1,1,1,-1,-1,1,1,-1,1,-1,1];%13位巴克码

tao=10e-6;%脉冲宽度10μs

fc=28e6;%调频信号起始频率

f0=30e6;

fs=100e6;%采样频率100MHz

ts=1/fs;

B=4e6;%调频信号带宽

t_tao=0:

1/fs:

tao-1/fs;

N=length（t_tao）;

k=B/fs*2*pi/max（t_tao）;

n=length（code）;

pha=0;

s=zeros（1,n*N）;

fori=1:

n;

ifcode（i）==1

pha=pi;

elsepha=0;

end

s（1,（i-1）*N+1:

i*N）=cos（2*pi*fc*t_tao+k*cumsum（t_tao）+pha）;

end

t=0:

1/fs:

13*tao-1/fs;

figure

（1）,subplot（2,1,1）,plot（t,s）,xlabel（'t（单位:

s）'）,title（'混合调制信号（13位巴克码+线性调频）'）;

s_fft_rsult=abs（fft（s（1:

N）））;

subplot（2,1,2）,plot（（0:

fs/N:

fs/2-fs/N）,abs（s_fft_result（1:

N/2）））,xlabel（'频率（单位：

Hz）'）,title（'码内信号频谱'）;

%%%%%%%%%%%%%%%%生脉冲压缩系数%%%%%%%%%%%%%%%%%%%

%____________正交解调__________________%

N=tao/ts;

n=0:

N-1;

s1=s（1:

N）;

local_oscillator_i=cos（n*f0/fs*2*pi）;%i路本振信号

local_oscillator_q=sin（n*f0/fs*2*pi）;%q路本振信号

fbb_i=local_oscillator_i.*s1;%i路解调

fbb_q=local_oscillator_q.*s1;%q路解调

window=chebwin（51,40）;

[b,a]=fir1（50,2*B/fs,window）;

fbb_i=[fbb_i,zeros（1,25）];

fbb_q=[fbb_q,zeros（1,25）];

fbb_i=filter（b,a,fbb_i）;

fbb_q=filter（b,a,fbb_q）;

fbb_i=fbb_i（26:

end）;%截取有效信息

fbb_q=fbb_q（26:

end）;%截取有效信息

fbb=fbb_i+j*fbb_q;

%______产生理想线性调频脉冲压缩匹配系数___________%

M=131072;%因为回波信号数据长度位3600点，所以利用FFT做4096点FFT

D=B*tao;

match_filter_1=ts*fliplr（conj（fbb））*sqrt（D）*2/tao;

match_filter_1_fft=fft（match_filter_1,M）;%第一次脉冲压缩处理匹配系数

figure

（2）,

subplot（2,1,1）,plot（real（match_filter_1_fft））,title（'脉冲压缩系数（实部）'）;

subplot（2,1,2）,plot（imag（match_filter_1_fft））,title（'脉冲压缩系数（虚部）'）;

N=length（s）;

n=0:

N-1;

local_oscillator_i=cos（n*f0/fs*2*pi）;%i路本振信号

local_oscillator_q=cos（n*f0/fs*2*pi）;%q路本振信号

fbb_i=local_oscillator_i.*s;%i路解调

fbb_q=local_oscillator_q.*s;%q路解调

window=chebwin（51,40）;%这是采用50阶cheby窗的FIR低通滤波器

[b,a]=fir1（50,0.5,window）;

fbb_i=[fbb_i,zeros（1,25）];

fbb_q=[fbb_q,zeros（1,25）];

fbb_i=filter（b,a,fbb_i）;

fbb_q=filter（b,a,fbb_q）;

fbb_i=fbb_i（26:

end）;%截取有效信息

fbb_q=fbb_q（26:

end）;%截取有效信息

signal=fbb_i+j*fbb_q;

clearfbb_i;

clearfbb_q;

signal_fft=fft（signal,M）*2;

pc_result_fft=signal_fft.*match_filter_1_fft;

pc_result=ifft（pc_result_fft,M）;

figure（3）,plot（（0:

ts:

length（signal）*ts-ts）,pc_result（1:

length（signal）））,xlabel（'时间,单位:

s'）,title（'回波脉冲压缩处理结果'）;

clearlocal_oscillator_i;

clearlocal_oscillator_q;

t=tao*length（code）;

match_filter_2=2*ts*fliplr（conj（pc_result））*2/t;

match_filter_2_fft=fft（match_filter_2,M）;%第二次脉冲压缩处理匹配系数

figure,

subplot（2,1,1）,plot（real（match_filter_2_fft））,title（'脉冲压缩系数（实部）'）;

subplot（2,1,1）,plot（imag（match_filter_2_fft））,title（'脉冲压缩系数（虚部）'）;

clearfbb;

clearmatch_filter_1;

clearmatch_filter_2;

clearsignal;

clearsignal_fft;

clearpc_result;

clearpc_result_fft;

%%%%%%%%%%%%%%%%%%%%%产生雷达回波%%%%%%%%%%%%%%%%%%

f_frame=1e3;%雷达发射信号重频，单位Hz

T_frame=1/f_frame;

N_echo_frame=18;

f_doppler=3.5e3;%动目标的多普勒领串

t_mobj=200e-6;%动目标位置

echo_mobj_pulse=[zeros（1,t_mobj/ts）,s,zeros（1,（T_frame-t_mobj）/ts-length（s））];

echo_mobj=repmat（echo_mobj_pulse,1,N_echo_frame）;

t_doppler=0:

ts:

N_echo_frame*T_frame-ts;

s_doppler=cos（2*pi*f_doppler*t_doppler）;

s_echo_mobj=echo_mobj.*s_doppler;

t_fobj=450e-6;%固定目标位置

echo_fobj_pulse=[zeros（1,t_fobj/ts）,s,zeros（1,（T_frame-t_fobj）/ts-length（s））];

s_echo_fobj=repmat（echo_fobj_pulse,1,N_echo_frame）;

t_clutter=700e-6;%杂波位置

t_clutter_pulse=39e-6;

sigma=2;%瑞利分布canshu数sigma

t1=0:

ts:

t_clutter_pulse-ts;

rand（'state',0）;%把均匀分布伪随机发生器置为0状态

u=rand（1,length（t1））;

echo_clutter=0.08*sqrt（2*log（1./u））*sigma;%,*s

s_echo_clutter_pulse=[zeros（1,t_clutter/ts）,echo_clutter,zeros（1,（T_frame-t_clutter）/ts-length（echo_clutter））];

s_echo_clutter=repmat（s_echo_clutter_pulse,1,N_echo_frame）;

s_nosie=0.1*rand（1,N_echo_frame*T_frame/ts）;

s_echo=s_echo_mobj+s_echo_fobj+s_echo_clutter+s_nosie;

clears_echo_mobj;

clears_echo_fobj;

clears_echo_clutter;

clears_echo_clutter_pulse;

clears_nosie;

clearecho_mobj_pulse;

clearecho_mobj;

clearecho_fobj_pluse;

clearecho_clutter;

clears_doppler;

cleart_doppler;

%________正交解调_____________%

N=N_echo_frame*T_frame/ts;

n=0:

N-1;

local_oscillator_i=cos（n*f0/fs*pi）;%I路本振信号

local_oscillator_q=cos（n*f0/fs*pi）;%Q路本振信号

s_echo_i=local_oscillator_i.*s_echo;%I路解调

s_echo_q=local_oscillator_q.*s_echo;%Q路解调

window=chebwin（51,40）;%这是采50阶cheby窗的FIR低通滤波器

[b,a]=fir1（50,2*B/fs,window）;

s_echo_i=[s_echo_i,zeros（1,25）];

s_echo_q=[s_echo_q,zeros（1,25）];

s_echo_i=filter（b,a,s_echo_i）;

s_echo_q=filter（b,a,s_echo_q）;

s_echo_i=s_echo_i（26:

end）;%截取有效信息

s_echo_q=s_echo_q（26:

end）;%截取有效信息

s_echo_mf=s_echo_i+j*s_echo_q;

clears_echo_i

clearlocal_oscillator_i;

clearlocal_oscillator_q;

clears_echo_i;

clears_echo_q;

clearn;

%%%%%%%%%%%%%%%脉冲压缩处理%%%%%%%%%%%%%%%%%%%%%%%%

fori=1:

N_echo_frame

s_echo_fft_result=fft（s_echo_mf（1,（i-1）*T_frame/ts+1:

i*T_frame/ts）,M）;

s_pc_fft_1=s_echo_fft_result.*match_filter_1_fft;

s_pc_fft_2=s_pc_fft_1.*match_filter_2_fft;

s_pc_result（i,:

）=ifft（s_pc_fft_2,M）;

end

clears_echo_mf;

s_pc_result_1=s_pc_result';

s_pc_result_1=reshape（s_pc_result_1,1,N_echo_frame*M）;

figure,subplot（2,1,1）,plot（0:

ts:

length（s_pc_result_1）*ts-ts,real（s_pc_result_1））,

%N_echo_frame*T_frame-ts

xlabel（'t（单位:

s）'）,title（'脉冲压缩处理后结果（实部）'）;

subplot（2,1,2）,plot（0:

ts:

length（s_pc_result_1）*ts-ts,imag（s_pc_result_1））,

xlabel（'t（单位:

s）'）,title（'脉冲压缩处理后结果（虚部）'）;

%%%%%%%%%%%%%%%%%%%%%固定杂波对消处理%%%%%%%%%%%%%%%%

fori=1:

16

s_MTI_result（i,:

）=s_pc_result（i,:

）+s_pc_result（i+2,:

）-2*s_pc_result（i+1,:

）;

end

clears_pc_result;

clears_pc_result_1;

s_MTI_result_1=s_MTI_result';

s_MTI_result_1=reshape（s_MTI_result_1,1,（N_echo_frame-2）*M）;

figure,subplot（2,1,1）,plot（0:

ts:

length（s_MTI_result_1）*ts-ts,real（s_MTI_result_1））,

xlabel（'t（单位:

s）'）,title（'固定杂波对消后结果（实部）'）;

subplot（2,1,2）,plot（0:

ts:

length（s_MTI_result_1）*ts-ts,imag（s_MTI_result_1））,

xlabel（'t（单位:

s）'）,title（'固定杂波对消后结果（虚部）'）;

clears_MTI_result_1;

结论

使用Matlab进行雷达信号处理系统仿真，能迅速建立起系统模型，设计理念可以在任何细节上得到体现，建模时间短，模型简单、清晰，计算精度高，同时在系统设计的任何阶段都能够很方便地修改模型、评估结果和验证系统行为。

本文以某脉冲压缩雷达为实例，基于Matlab的雷达信号处理的仿真方法取得了较好的效果。

在雷达信号处理系统中系统级仿真占有极其重要的地位,经过系统级仿真能够保证产品在最高层次上的设计正确性。

由于外场模拟真实战场复杂电磁环境是非常困难的,同时也耗资巨大,所以利用计算机仿真技术的可控制性、可重复性、无破坏性、安全性、经济性等特点与优势对雷达电子对抗装备及其技术与战术运用等进行仿真与效能评估,是当前和未来雷达与电子对抗领域研究中的一种重要手段。

通过MATLAB软件进行仿真得到的仿真图如下所示：

图1

图2

图3

图4

图5

图6