实验一霍尔位置传感器及弯曲法杨氏模量的测定.docx

实验一霍尔位置传感器及弯曲法杨氏模量的测定.docx

《实验一霍尔位置传感器及弯曲法杨氏模量的测定.docx》由会员分享，可在线阅读，更多相关《实验一霍尔位置传感器及弯曲法杨氏模量的测定.docx（13页珍藏版）》请在冰豆网上搜索。

实验一霍尔位置传感器及弯曲法杨氏模量的测定

实验一霍尔位置传感器及弯曲法杨氏模量的测定

实验目的

1.掌握用米尺、游标卡尺、螺旋测微器、读数显微镜测量长度的方法

2.熟悉霍尔位置传感器的特性；

3.弯曲法测量黄铜（或可锻铸铁）的杨氏模量，并对霍尔位置传感器定标;

仪器和用具

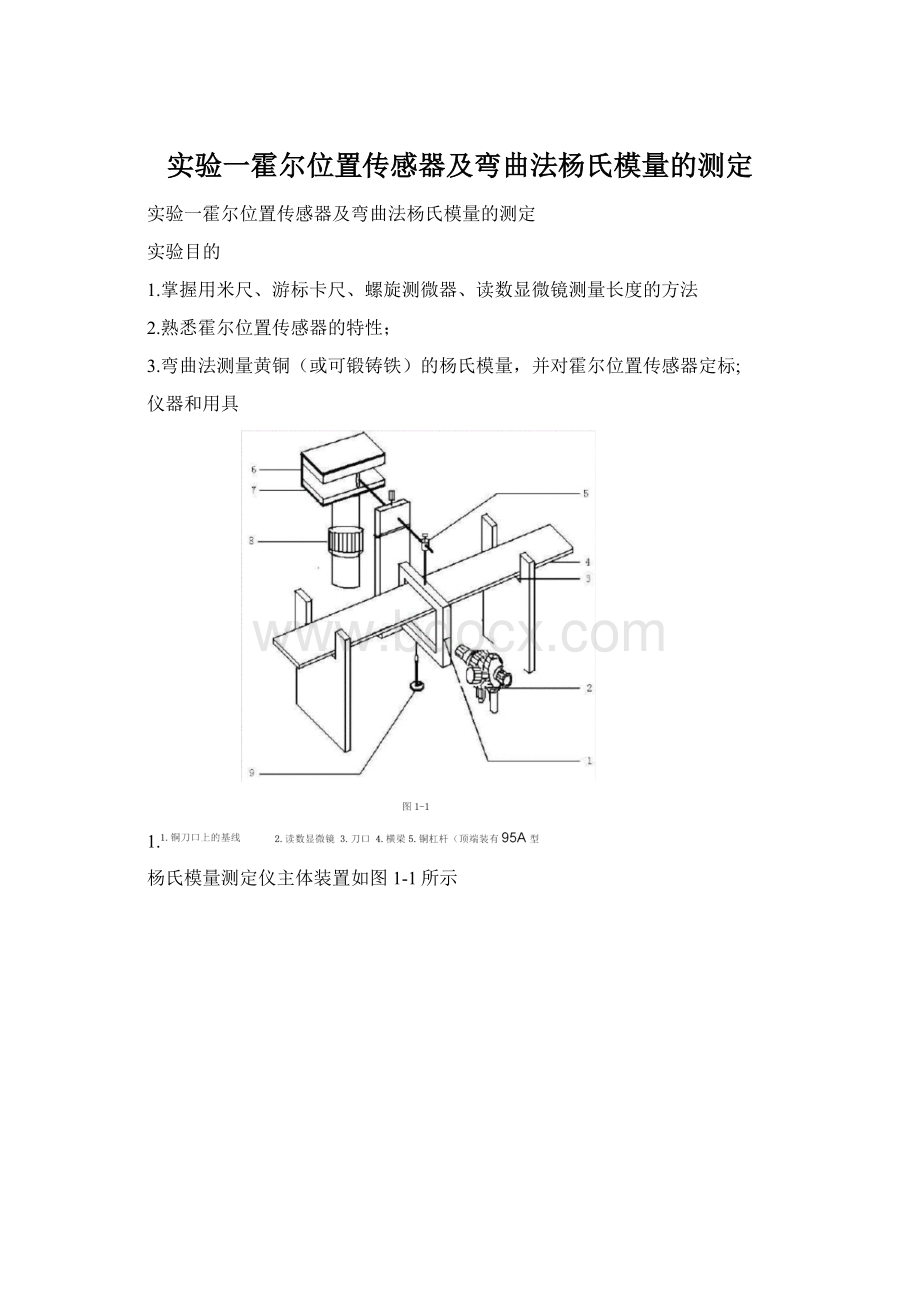
1.

杨氏模量测定仪主体装置如图1-1所示

图1-2实验装置的实物照片

2、其他用用具

米尺，游标卡尺，螺旋测微仪，砝码，待测材料（一根黄铜、一根可铸锻铁）

实验原理

1.霍尔位置传感器

霍尔元件置于磁感应强度为B的磁场中，在垂直于磁场方向通以电流I，则与这二

者相垂直的方向上将产生霍尔电势差UH：

UhKIB（1-1）

（1-1）式中K为元件的霍尔灵敏度。

如果保持霍尔元件的电流I不变，而使其在一个

均匀梯度的磁场中移动时，则输出的霍尔电势差变化量为：

dB

UhKIZ（1-2）

dZ

dZ

（1-2）式中Z为位移量，此式说明若QB为常数时，UH与Z成正比。

N

图1-3

为实现均匀梯度的磁场，可以如图1-3所示，两块相同的磁铁（磁铁截面积及表面磁感

应强度相同）相对放置，即N极与N极相对，两磁铁之间留一等间距间隙，霍尔元件平行

于磁铁放在该间隙的中轴上。

间隙大小要根据测量范围和测量灵敏度要求而定，间隙越小，磁场梯度就越大，灵敏度就越高。

磁铁截面要远大于霍尔元件，以尽可能的减小边缘效应影

响，提高测量精确度。

若磁铁间隙内中心截面处的磁感应强度为零，霍尔元件处于该处时，输出的霍尔电势差

应该为零。

当霍尔元件偏离中心沿Z轴发生位移时，由于磁感应强度不再为零，霍尔元件

也就产生相应的电势差输出，其大小可以用数字电压表测量。

由此可以将霍尔电势差为零时

元件所处的位置作为位移参考零点。

霍尔电势差与位移量之间存在对应关系，当位移量较小（2mm），这一对应关

系具有良好的线性。

2、杨氏模量

固体、液体及气体在受外力作用时，形状或体积会发生或大或小的改变，称之为形变。

当外力不太大时，引起的形变也不会太大，若撤掉外力，形变随之会消失，这种形变称为弹

性形变。

如一段固体棒，在其两端沿轴方向施加大小相等，方向相反的外力F,其长度I发生改

变厶1,以S表示横截面面积，称F/S为应力，相对长变（△I/I）为应变，在弹性限度内，根据胡克定律有

存在一个中性面，面以上的部分发生压缩，面以下的部分发生拉伸。

总体来说，待测样品将

发生应变，可用杨氏模量来描述材料的性质，杨氏模量为

公式

其中：

d为两刀口之间的距离，M为所加砝码的质量，a为梁的宽度，戴尔特Z为梁中心由

于外力作用而下降的距离，g为重力加速度。

向体.權徉矗气怵在燮外力作用时，环与牺馭刍发生或為或木的谨变.铭之为矽J春

当外力不丈大时，引起前底变也不金衣大，若撇却外力.懸变能之衾消先.赵冲惑变称为弹

性戦-

御一段同翳.在共两喘汨牯厅向俺姐天小卅警，$旬柑辰的外力码生改变

M肚除示崔藏而両积・祢冊知卿力，袖对宦娈CAIO为唤祥强性限曳th根卿

克定律有

FA/

L-Y—

SJ

F称为杨氏蟆注H数值与封料性顼有关”丈［圈2碌.衽持测徉品憧牛潢小劣曲时.艇

屮存在一个屮W\t而吐卜的邯分发生圧縮’而厘下的部分发生栓伸”蔥律说来*特测澤品

将发生唤可用擀氏橈荒来描吗村料的性质，杨氏機祖为

梵申I砒西人口之何的瓯阀，対为所加戢码的记L应为麟朗厚僮，&为梁的血度*g

梁电心由丁■外力作用而下降的厕虬琴为車力加園匕

实验内容

1基本内容：

测量黄铜样品的杨氏模量和霍尔位置传感器的定标。

（1）调节三维调节架的调节螺丝，使集成霍尔位置传感器探测元件处于磁铁中间的位置。

（2）用水准器观察是否在水平位置，若偏离时可以用底座螺丝调节。

（3）调节霍尔位置传感器的毫伏表。

磁铁盒下的调节螺丝可以使磁铁上下移动，当毫伏表数值很小时，停止调节固定螺丝，最后调节调零电位器使毫伏表读数为零。

（4）调节读数显微镜，使眼镜观察十字线及分划板刻度线和数字清晰。

然后移动读数

显微镜前后距离，使能够清晰看到铜架上的基线。

转动读数显微镜的鼓轮使刀口架的基线与

读数显微镜内十字刻度线吻合，记下初始读数值。

（5）逐次增加砝码（每次增加10g砝码），相应从读数显微镜上读出梁的弯曲位移也乙及数字电压表相应的读数值5（单位mV。

以便于计算杨氏模量和霍尔位置传感器进行定标。

在进行测量之前，要求符合上述安装要求，并且检查杠杆的水平、刀口的垂直、挂砝码的刀口处于梁中间，要防止外加风的影响，杠杆安放在磁铁的中间，注意不要与金属

外壳接触，一切正常后加砝码，使梁弯曲产生位移--;精确测量传感器信号输出端的数值

与固定砝码架的位置Z的关系，也就是用读数显微镜对传感器输出量进行定标，检验二-

的关系。

（6）测量横梁两刀口间的长度d及测量不同位置横梁宽度b和梁厚度a。

（7）用逐差法按照公式（3）进行计算，求得黄铜材料的杨氏模量，并求出霍尔位置传感器的灵敏度―一丿，并把测量值与公认值进行比较。

2•选作内容：

用霍尔位置传感器测量可锻铸铁的杨氏模量。

查：

丿如一'''J-y-1■"''<■

数据记录与处理

1•霍尔位置传感器的定标

利用读数显微镜的读数和位置传感器输出电压U,用图解法求出霍尔位置传感器的灵敏度

公式

表1霍尔位置传感器静态特性测量

序号i

1

2

3

4

5

6

7

8

M（g）

40

50

60

70

80

90

100

110

Z（mm）

U（mV）

2.测量杨氏模量

用逐差法求出加砝码质量M时，对应的梁中心由于外力作用而下降的距离戴尔特Z。

序号i

1

2

3

4

平均值

公式

计算平均值及不确定度:

公式

其他量：

d=

序号

1

2

3

4

5

6

7

8

9

10

梁宽b（mm

b=

d=

序号

1

2

3

4

5

6

7

8

9

10

梁厚a（mm

利用式（4）计算，求得黄铜材料的杨氏模量及总不确定度

公式

把测量结果与公认值（数值）进行比较

【或据记录与处理】

1.龜尔位宣传总辭的定标

別用谀数显微桃的谀数和位鱼传感器输出电氏⑺用阁解汕求4］宦尔位置传感舒的灵瞰

«|斥尔位匿何◎黑帽&笛性測1

序号d

1

■■■■■■■■■■■■■■■■■

2

3

4

s

6

7

s

W）

40

50

60

70

n

90

100

110

Z（mfn）

U（mv）

2.测:

ft赫氏鮭

2.2

2.1用逐差法求出加“码质：

ttM时.对应的梁屮心由丁外力作用而下降的斬紅乙

净号f

1

2

3

4

平均直

q・爲4—石（T

汁却平均值及不備定反'

AZ=1^^缶为遂差值个数，此处＞1=4）

tf（AZ）=^（AZ）+ui（Zz）

2.3

/=-cm

序号

1

2

3

4

5

6

7

9

10

t基心m

JT4llJ45i7fL^I0

2.4利刊戒（4）求帑甘啊材科的桶氐柑梵及膿否喘定愷

Y=Y^2u（T）

工哎拦#1M：

培平与公认隹＜I«5X心Mm》进行比校,

【注意事项】

（1）梁的厚度必须测准确。

在用千分尺测量黄铜厚度a时，将千分尺旋转时，当将要与金属接触时，必须用微调轮。

当听到答答答三声时，停止旋转。

有个别学生实验误差较大，其原因是千分尺使用不当，将黄铜梁厚度测得偏小；

（2）读数显微镜的准丝对准铜挂件（有刀口）的标志刻度线时，注意要区别是黄

铜梁的边沿，还是标志线;

（3）霍尔位置传感器定标前，应先将霍尔传感器调整到零输出位置，这时可调节

电磁铁盒下的升降杆上的旋钮，达到零输出的目的，另外，应使霍尔位置传感器的探头处于

两块磁铁的正中间稍偏下的位置，这样测量数据更可靠一些；

（4）加砝码时，应该轻拿轻放，尽量减小砝码架的晃动，这样可以使电压值在较

短的时间内达到稳定值，节省了实验时间；

（5）实验开始前，必须检查横梁是否有弯曲，如有，应矫正。

【思考题】

1.弯曲法测杨氏模量实验，测量误差主要有哪些估算各因素的不确定度

2.利用霍尔传感器法测位移有什么优点弯曲法测杨氏模量实验，主要测量误差有哪些

请估算各测量的不确定度

3.在本实验中最需要保证的实验条件是什么为什么要有限制的增加砝码

4.实验中如何确定支撑横梁的两刀口是否平行

k弯甘法测杨氏模址实验，测甘眾差主匪冇哪些丫优秣齐丙橫曲不嗚定！

匕

九用霍尔世圧祷感落決測垃移市什亘优.点？

内一曲決测畅氐挾捷买验.主翌阀it富葢冇那些T忙估尊丼剧金绘的平确足便w

3-在本实验中J6需哽煤证旳实验条件是忡么丁为什么耍冇阻制地曲加吐码f

比实捡屮如阿诵宦艾撐潢第的两力口足百T行？

【参考资料】

[1]

漆安慎

杜婵英

《力学》高等教育出版社

[2]

方佩敏

《新编传感器原理、应用、电路详解》

电子工业出版社

[3]

游海洋

赵在忠

陆申龙《霍尔位置传感器测量固体材料的杨氏模量》

《物理

实验》，第20卷第8期

【附录】弯曲法测量杨氏模量公式的推导

固体、液体及气体在受外力作用时，形状与体积会发生或大或小的改变，这统称为形变。

当外力不太大，因而引起的形变也不太大时，撤掉外力，形变就会消失，这种形变称之为弹

性形变。

弹性形变分为长变、切变和体变三种。

定律有:

（1-3）

丫称为杨氏模量，其数值与材料性质有关。

所以整体说来，可以理解横梁发生长变，即可以用杨氏模量来描写材料的性质。

如图1-4所示，虚线表示弯曲梁的中性面，易知其既不拉伸也不压缩，取弯曲梁长为dx

的一小段:

（R（x）y）ddx

所以

所以应变为：

根据虎克定律有：

又

所以

对中性面的转矩为:

积分得：

对梁上各点，有：

因梁的弯曲微小：

所以有:

dx

R（x）；

加心dx阳刃琵dx总严

dFYy

dSR（x）；

dSbdy；

dF（x）

Yby

R（x）

dy

d（x）dFy

dy

（x）

1

R（x）

4y2dyYA^3

2R（x）12R（x）；

y（x）

3

2-

1y（x）2；

y（x）0；

R（x）

（1-3）

（4）

梁平衡时，梁在x处的转矩应与梁右端支撑力

Mg

2对x处的力矩平衡,

所以有:

（x）

Mg（d

2（2

x）

根据（3）、（4）、（5）式可以得到:

y（x）

6Mg

Yba3

解上面的微分方程得到:

将x—代入上式，得右端点的

2

又

所以，杨氏模量为：

y（x）

3Mg

Yba3

.—213

（—xx

23

y值：

y

Mg—3

3

4Yba

；

y

Z；

Y

—3Mg

4a3b

Z