微波滤波器讲稿.docx

微波滤波器讲稿.docx

《微波滤波器讲稿.docx》由会员分享，可在线阅读，更多相关《微波滤波器讲稿.docx（20页珍藏版）》请在冰豆网上搜索。

微波滤波器讲稿

第七章微波滤波器

§7-1概述

微波滤波器的分类：

1．微波滤波器按其特性不同可分为:

低通、高通、带通和带阻滤波器。

2．按结构不同又可分为:

同轴线滤波器、波导滤波器和微带、带状线滤波器。

微波滤波器中所研究的问题：

1．分析问题：

已知滤波器的结构和元件值计算它的插入衰减频率特性；

2．综合问题：

由给定的滤波器插入衰减频率特性来确定滤波器的网络结构和元件值。

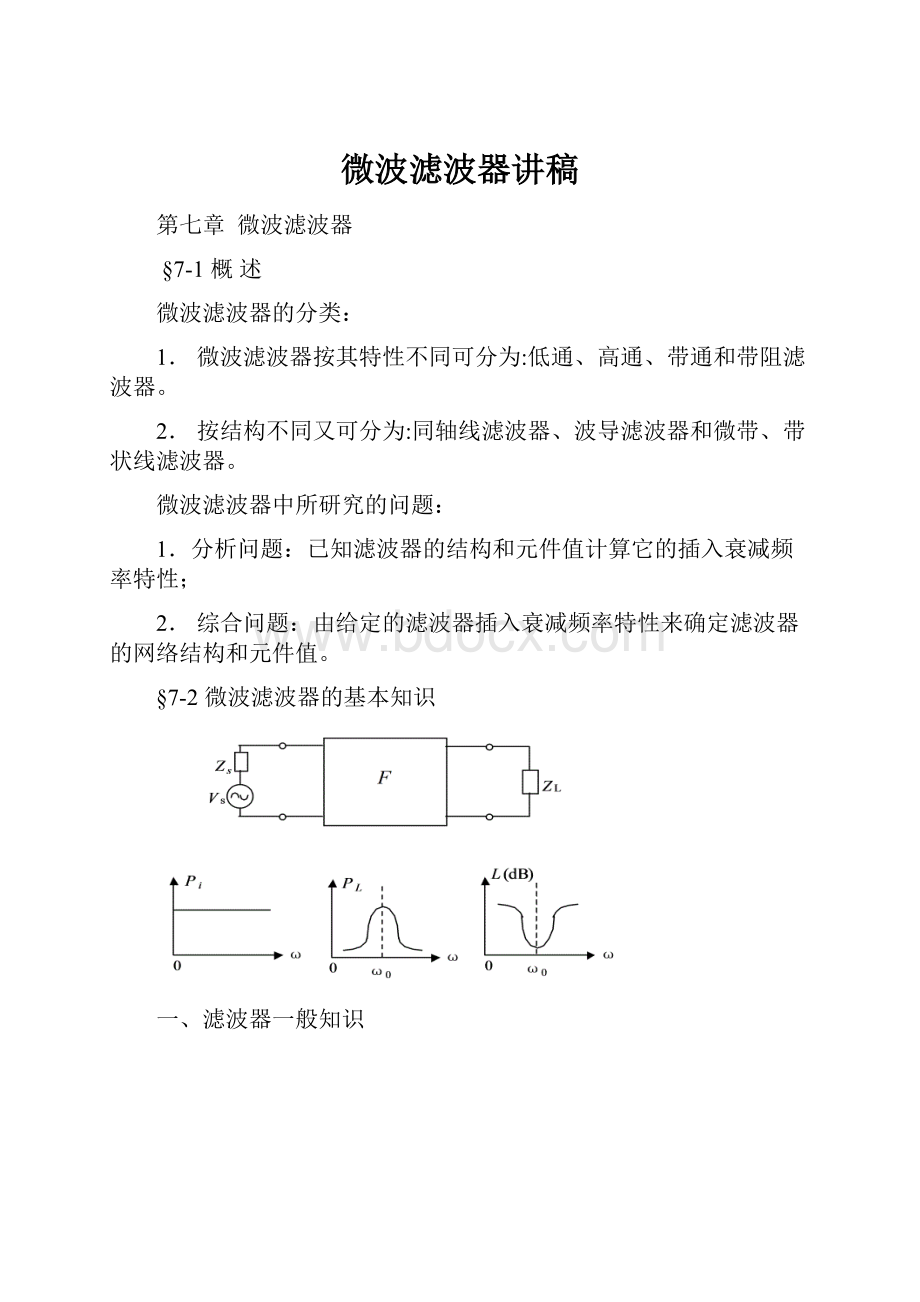
§7-2微波滤波器的基本知识

一、滤波器一般知识

按照衰减特性的不同,低频滤波器可分为:

低通、高通、带通和带阻滤波器五大类。

衰减：

输入功率Pi与负载所吸收功率PL之比。

通常用A或A（ω）表示，即：

（7.1）

若用dB表示，则可写成

（dB）（7.2）

二、微波滤波器的主要技术指标

衡量微波滤波器性能的主要技术指标有:

1.截止频率ωC。

2.通带内允许的最大衰减Lp。

3．阻带内最小衰减LS及其相应的阻带边频ωS。

4.寄生通带,即阻带内出现的不希望有的通带。

三、微波滤波器的综合设计

图7.5微波滤波器的设计程序框图

（一）低通滤波器的三种典型衰减特性

图7.6低通滤波器的三种典型衰减特性

理想的滤波特性,用有限个元件的电抗网络是不可能实现的。

实际滤波器的衰减特性,只能是逼近理想滤波器的衰减特性。

逼近函数的种类很多,实际中用得最多的只有三种,其相应的滤波器分别称为最平坦式滤波器、切比雪夫式滤波器和椭圆函数式滤波器。

（二）低通原型滤波器

1．低通原型滤波器及其衰减特性

定义：

低通原型滤波器就是指以归一化频率ω′＝ω／ωc为自变量的衰减特性L（ω′）为基础综合出来的低通滤波器。

2.最平坦式低通原型滤波器的综合设计步骤

（1）由要求的LP、LS和ωC′=1,ωS′=ωS/ωC求k和n。

最平坦式低通滤波器衰减特性为L（ω）=10lg（1+k2ω2n）,因为通带内最大衰减LP对应着截止频率ωC,而阻带内最小衰减LS对应着阻带边频,所以

（7．3）

（7．4）

对于最平坦式低通原型滤波器，衰减特性为

（7．6）

（7．7）

通常取通带内最大衰减LP＝3dB,则由（7.6）式可求得k＝１，于是（7.7）式可写成:

（7．8）

由（7.8）式可求得梯形结构电路元件数n。

为方便,现已将（7.8）式以n作参变量制成LS～ωS′的曲线,如图7.8所示。

由要求的LS和ωS′即可查得n值。

（2）由n决定梯形电路及其各元件的归一化数值（表7-1）。

由表7-1可见,所有gn+1＝１,即滤波器的负载电阻（或电导）均与信号源内阻（或内电导）相等这是由于最平坦式衰减特性要求在频率为零时衰减为零，由于此时滤波器相当于一条传输线，所以只有负载阻抗匹配时才能使衰减为零，即gn+1＝１。

为了对各种信号源的内阻具有通用性,电路元件的阻抗值是对信号源内阻归一化的,而不是真正的元件值。

综合设计的结果表明:

从同一衰减持性出发综合设计出来的低通原型总共有两个,而且是互为对偶的梯形电路,一为电感输入式,一为电容输入式,它们的归一化元件值gk（k=1,2,…n,n+1）一一对应相等。

在上图中,若负载与gn并联,则用gn＋1表示负载电阻；如负载与gn串联,则用gn+1表示负载电导。

即阻抗与导纳相间出现。

对于切比雪夫式低通原型，应用表7-2时,要注意负载gn+1的两个特点:

（1）当n＝奇数时,gn+1＝１；当n=偶数时,gn+1≠1。

这是由于n=奇数时,衰减曲线通过原点,即当ω′＝0时,L（ω′）＝0,所以要负载匹配,gn+1＝１；n=偶数时,曲线不通过原点,即当ω′＝0时,L（ω′）≠0,所以gn+1≠１。

（2）gn+1有时代表归一化负载电阻,有时代表归一化负载电导。

其规则是:

当gn+1与gn并联时,gn+1表示负载电阻；当gn+1与gn串联时,则用gn+1表示负载电导。

表7-1最平坦式低通原型滤波器的归一元件值（LP＝3dB）

n

g1

g2

g3

g4

g5

g6

g7

g8

g9

g10

g11

1

2

3

4

5

6

7

8

9

10

2.00

1.414

1.000

0.7654

0.6180

0.5176

0.4450

0.3902

0.3473

0.3129

1.000

1.414

2.000

1.848

1.618

1.414

1.247

1.111

1.000

0.9080

1.00

1.00

1.84

2.00

1.93

1.80

1.66

1.532

1.414

1.000

0.765

1.618

1.932

2.000

1.962

1.879

1.782

1.000

0.618

1.414

1.802

1.962

2.000

1.975

1.000

0.517

1.247

1.663

1.879

1.975

1.000

0.445

1.111

1.532

1.782

1.000

0.390

1.000

1.414

1.000

0.3473

0.9080

1.000

0.3129

1.000

表7-2切比雪夫低通原型滤波器元件的归一化值（g0＝１）

（a）LP＝0.1dB

n

g1

g2

g3

g4

g5

g6

g7

g8

g9

g10

g11

1

2

3

4

5

6

7

8

9

10

0.3052

0.8430

1.0315

1.1088

1.1468

1.1681

1.1811

1.1897

1.1956

1.1999

1.0000

0.6220

1.1474

1.3061

1.3712

1.4039

1.4228

1.4346

1.4425

1.4481

1.3554

1.0315

1.7703

1.9750

2.0562

2.0966

2.1199

2.1345

2.1444

1.0000

0.8180

1.3712

1.5170

1.5733

1.6010

1.6167

1.6265

1.355

1.146

1.902

2.096

2.169

2.205

2.225

1.000

0.861

1.422

1.564

1.616

1.641

1.3554

1.1811

1.9444

2.1345

2.2046

1.000

0.877

1.442

1.582

1.355

1.195

1.962

1.000

0.885

1.355

（b）LP＝0.5dB

n

g1

g2

g3

g4

g5

g6

g7

g8

g9

g10

g11

1

2

3

4

5

6

7

8

9

10

0.6986

1.4029

1.5963

1.6703

1.7058

1.7254

1.7372

1.7451

1.7504

1.7543

1.0000

0.7071

1.0967

1.1926

1.2296

1.2479

1.2583

1.2647

1.2690

1.2721

1.9841

1.5963

2.3661

2.5408

2.6064

2.6381

2.6564

2.6678

2.6754

1.0000

0.8419

1.2296

1.3137

1.3444

1.3590

1.3673

1.3725

1.984

1.705

2.475

2.638

2.696

2.723

2.739

1.000

0.869

1.258

1.338

1.367

1.380

1.9841

1.7372

2.5093

2.6678

2.7231

1.000

0.879

1.269

1.348

1.984

1.750

2.523

1.000

0.884

1.984

（c）LP＝1.0dB

n

g1

g2

g3

g4

g5

g6

g7

g8

g9

g10

g11

1

2

3

4

5

6

7

8

9

10

1.0177

1.8219

2.2036

2.0991

2.1349

2.1546

2.1664

2.1744

2.1797

2.1836

1.0000

0.6850

0.9941

1.0644

1.0911

1.1041

1.1116

1.1161

1.1192

1.1213

2.6599

2.2036

2.8311

3.0009

3.0634

3.0984

3.1107

3.1215

3.1286

1.0000

0.7892

1.0911

1.1518

1.1736

1.1839

1.1897

1.1933

2.659

2.134

2.936

3.0934

3.1488

3.1747

3.1890

1.000

0.810

1.1116

1.1696

1.1897

1.1990

2.6599

2.1664

2.9685

3.1215

3.1738

1.0000

0.8175

1.1192

1.1763

2.6599

2.1797

2.9824

1.0000

0.8210

2.6599

例7.1〕如要求截止频率fc＝１GHz,LP＝3dB,在fS=1.5GHz处,LS≥30dB,试确定最平坦式低通原型滤波器的结构及各元件的归一化值。

解:

（1）n值的确定

图7.11最平坦式低通原型滤波器电路图

由图7.8中可以查得与LS=30dB,ωS′－1＝0.5相对应的点位于n＝8和n＝9两条曲线之间,取n＝9。

（2）确定各元件的归一化值

由表7-1查得n＝9时:

g1=g9=0.3473，g2=g8=1.0000，g3=g7=1.532，g4=g6=1.8790，g5=2.000，g10=1.000（3）最平坦式低通原型滤波器电路如图7.11所示。

〔例7.2〕如要求截止频率fc＝3GHz,LP＝0.1dB,在fS=4.5GHz处,LS≥30dB,试确定切比雪夫式低通原型滤波器的结构及各元件的归一化值。

图7.12切比雪夫式低通原型滤波器电路图

解:

（1）n值的确定

由图7.8中可以查得与LS=30dB,ωS′－1＝0.5相对应的点在n＝6和n＝7之间,取n＝7。

（2）确定各元件的归一化值由表7-2（a）中n＝７查得:

g1=g7=1.1181，g2=g6=1.4228，g3=g5=2.0966，g4=1.5733，g8=1.0000。

（3）画出切比雪夫式低通原型滤波器电路如图7.12所示。

（三）频率变换

1．低通滤波器与低通原型的频率变换欲使图（a）变成图（b）,则要求

ω＝0、ωC、ωS、∞

ω′＝0、1、ωS′、∞

一一对应,为此,采用如下频率变换式:

另外,还要求在上述对应点上衰减量L相等,为此则要求网络中对应元件在两种频率变量下具有相同的阻抗,用公式表示为:

（7．10）

上式称为等衰减条件。

在等衰减条件下,有

式中Lk′和Ci′是实际滤波器元件的归一化值。

于是得到

（7．11）求元件的真实值,只需对信号源内阻R0反归一化即可,即:

（7．12）而实际负载则由原型电路的负载性质所确定。

若gn＋１与gn并联,则

（7．13a）

若gn＋１与gn串联,则

（7．13b）

图7.14低通原型和低通滤波器的对应电路

图7.14给出了电感输入式低通原型和实际低通滤波器的对应电路。

2.高通滤波器与低通原型的频率变换

为使图（a）变成图（b）,须使

ω＝0、ωS、ωC、∞

ω′＝－∞、-ωS′、-1、0

的点一一对应,为此采用频率变换式:

运用等衰减条件（7.8）式,得:

可见,低通原型中的电感变换为高通滤波器中的电容,而低通原型中的电容,变换为高通滤波器中的电感。

高通滤波器元件的归一化值为:

（7．15）

上式对信号源内阻R0反归一化,得元件的真值:

负载性质的判别同前。

低通原型和高通滤波器的对应电路如上图所示。

3.带通滤波器与低通原型的频率变换

为使图（a）变成图（b）,需使

ω＝0、ωS1、ωC1、ω0、ωC2、ωS2、+∞

ω′＝-∞、-ωS′、-1、0、1、ωS′、＋∞

一一对应,为此需采用以下频率变换式:

式中：

为相对带宽,

为中心频率。

运用等衰减条件得:

（7．18a）

（7．18b）

由此可得串、并联谐振电路的归一化元件值：

（7．19）

可见低通原型中的串联电感变换成为带通滤波器中的串联谐振电路,并联电容变换成为带通滤波器中的并联谐振电路,且串谐电路的谐振频率与并谐电路的谐振频率相等,都等于

即:

图7.18带通滤波器的归一化电路

元件真实值的求得只需将Lk′、Ck′、Li′、Ci′对信号源内阻反归一化即可,负载性质判别同前。

带通滤波器的归一化电路如图7.18所示。

4.带阻滤波器与低通原型的频率变换

为了将图（a）变成图（b）,要求

ω＝0、ωC1、ωS1、ω0、ωS2、ωC2、+∞

ω′＝+0、1、ωS1′、±∞、-ωS2′、-1、-0

一一对应。

为此采用如下频率变换:

图7.19带阻滤波器的频率变换

（7．21）

式中

为中心频率；

为相对带宽。

运用等衰减条件得:

因此可得：

（7．22）

可见：

低通原型中的串联电感变成了带阻滤波器的并谐电路；并联电容变成了串谐电路。

且由式（7.22）可知,串谐支路的谐振频率与并谐支路的谐振频率相等,且均等于ω0，即:

（7．23）

元件真实值的计算和负载性质的判断方法同前。

带阻滤波器的归一化电路如图7.20所示。

图7.20带阻滤波器的归一化电路

（四）滤波器电路的微波实现

前面综合设计出的滤波器都是由集中元件的电感L和电容C组成的。

在微波滤波器中关键是如何用一定的微波结构即分布参数元件代替低频滤波器中的集中参数元件。

通常把这一过程称为滤滤器电路的微波实现。

下面几节,我们将分别讨论微波低通、带通和带阻滤波器的微波实现方法。

§7-3微波低通滤波器

低通滤波器的电路结构是由一些串联电感和一些并联电容组成的。

在第二章中讨论微带集中元件的实现时我们知道,实现集中电感和电容的方法通常有两种:

一种是利用短路短线和开路短线来实现;另一种是用高、低阻抗线实现。

图7.21（n=5）电感输入方式同轴低通滤波器

一、微波低通滤波器

图7.22电容输入式微带低通滤波器

〔例7.3〕设计一个切比雪夫式同轴型微波低通滤波器,要求其截止频率fC＝3.6GHz,带内最大衰减LP=0.1dB,在阻带边频fS=6.4GHz处,LS≥30dB,输入、输出同轴线的特性阻抗均为Z0=50Ω,其内导体直径d=0.7cm,外导体内直径D=1.6cm。

解:

（1）根据技术指标LS、ωS′确定元件数n

由LS≥30dB,从图7.10（a）中查得n＝5

（2）求低通原型滤波器元件的归一化值

由表7-2查得n＝5时低通原型滤波器元件的归一化值为:

g1=g5=1.1463，g2=g4=1.3712，g3=1.9750，g6=1.0000

（3）选定梯形电路的形式,计算各元件的真实值

选用电容输入式电路,如图7.23（a）所示。

由（7.12）式求得各元件的真实值:

图7.23[例7.3]用图

（4）选择各段传输线的特性阻抗并计算各段的长度

图7.23（b）给出了该同轴型低通滤波器的具体结构。

如选择l2、l4段的高特性阻抗为:

可得:

则

由（3.24）式可求得:

如选择l1、l3、l5段的低特性阻抗为:

则

由（3.24）式可求得: